人教版八年级数学上册第十四章14.1.4 整式的乘法课件(3课时共91张)
文档属性
| 名称 | 人教版八年级数学上册第十四章14.1.4 整式的乘法课件(3课时共91张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-25 18:34:26 | ||
图片预览











文档简介
课件91张PPT。14.1 整式的乘法
14.1.4 整式的乘法单项式与单项式、多项式相乘1.幂的运算性质有哪几条? 同底数幂的乘法法则:am·an=am+n ( m、n都是正整数).幂的乘方法则:(am)n=amn ( m、n都是正整数).积的乘方法则:(ab)n=anbn ( m、n都是正整数).2.计算:(1)x2 · x3 · x4= ;
(2)(x3)6= ; (3)(–2a4b2)3= ;
(4) (a2)3 · a4= ;
(5) .x9x18–8a12b6a101回
顾旧知1. 掌握单项式与单项式、单项式与多项式相乘的运算法则.2. 能够灵活地进行单项式与单项式、单项式与多项式相乘的运算. 素养目标单项式与单项式相乘 光的速度约是3×105km/s,太阳光照射到地球上需要的时间大约是5×102s,你知道地球与太阳的距离约是多少吗?地球与太阳的距离约是(3×105)×(5×102)km.(3×105)×(5×102)=(3×5)×(105×102)=15×107. 乘法交换律、结合律 同底数幂的乘法这样书写规范吗?不规范,应为1.5×108. 怎样计算(3 ×105)×(5 ×102)?计算过程中用到了哪些运算律及运算性质? 如果将上式中的数字改为字母,比如ac5 ·bc2,怎样计算这个式子?根据以上计算,想一想如何计算单项式乘以单项式? ac5 · bc2 =(a ·b) ·(c5·c2) (乘法交换律、结合律)
=abc5+2 (同底数幂的乘法)
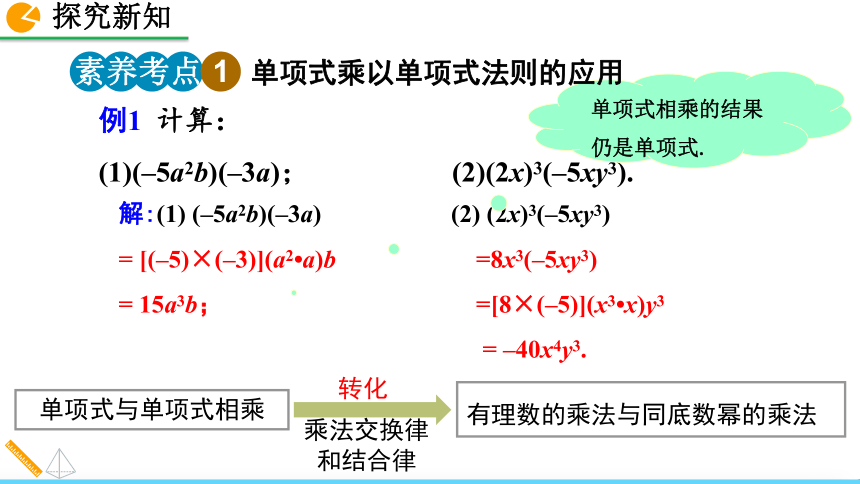
=abc7. 单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.单项式与单项式的乘法法则例1 计算:
(1)(–5a2b)(–3a); (2)(2x)3(–5xy3).解:(1) (–5a2b)(–3a)
= [(–5)×(–3)](a2?a)b
= 15a3b;(2) (2x)3(–5xy3)
=8x3(–5xy3)
=[8×(–5)](x3?x)y3
= –40x4y3.单项式与单项式相乘有理数的乘法与同底数幂的乘法单项式乘以单项式法则的应用1. 在计算时,应先确定积的符号,积的系数等于各因式系数的积;
2. 注意按顺序运算;
3. 不要漏掉只在一个单项式里含有的字母因式;
4. 此性质对三个及以上单项式相乘仍然适用.1.下面各题的计算结果对不对?如果不对,应当怎样改正?
(1)3a3 ·2a2=6a6 ( ) 改正: .
(2) 2x2 ·3x2=6x4 ( ) 改正: .
(3)3x2 ·4x2=12x2 ( ) 改正: .
(4) 5y3·3y5=15y15 ( ) 改正: .3a3 ·2a2=6a5 3x2 ·4x2=12x4 5y3·3y5=15y8 ×××2.计算:(1) 3x2 ·5x3 ; (2)4y ·(–2xy2); (3) (–3x)2 ·4x2 ; (4)(–2a)3(–3a)2.解:(1)原式=(3×5)(x2·x3)=15x5; (2)原式=[4×(–2)](y·y2) ·x= –8xy3; (3) 原式=9x2·4x2 =(9×4)(x2·x2)=36x4; (4)原式= –8a3·9a2 =[(–8)×9](a3·a2)= –72a5单独因式x别漏乘、漏写有乘方运算,先算乘方,再算单项式相乘.例2 已知–2x3m+1y2n与7xn–6y–3–m的积与x4y是同类项,求m2+n的值.解:∵–2x3m+1y2n与7xn–6y–3–m的积与x4y是同类项,∴m2+n=7.方法总结:单项式乘以单项式就是把它们的系数和同底数幂分别相乘,结合同类项的定义,列出二元一次方程组求出参数的值,然后代入求值即可.利用单项式乘法的法则求字母的值3. 已知 求 的值.解得:∴m、n的值分别是m=1,n=2.解:单项式与多项式相乘如图,试求出三块草坪的总面积是多少? 如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____. papcpb 如果把它看成一个大长方形,那么它的边长为________,面积可表示为_________. p(a+b+c)(a+b+c) 如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____. 如果把它看成一个大长方形,那么它的面积可表示为_________. p(a+b+c)pa+pb+pcp(a+b+c)p (a + b+ c)pb+pcpa+根据乘法的分配律 单项式与多项式相乘,就是用单项式乘多项式的每一项,再把所得的积相加.单项式乘以多项式的法则例3 计算:(1)(–4x)·(2x2+3x–1); 解:(1)(–4x)·(2x2+3x–1)==–8x3–12x2+4x;(–4x)·(2x2)(–4x)·3x(–4x)·(–1)++(2)原式单项式与多项式相乘单项式与单项式相乘利用单项式乘以多项式的法则进行运算解题步骤:1.用单项式去乘多项式的每一项,结果是一个多项式,项数与因式中多项式的项数相同.2.含有混合运算的应注意运算顺序,有同类项的必须合并同类项,从而得到最简结果.①②③4.下列各题的解法是否正确,如果错了,指出错在什么地方,并改正过来。×××漏了单独字母漏乘1符号没有变化例4 先化简,再求值:3a(2a2–4a+3)–2a2(3a+4),
其中a=–2.当a=–2时,解:3a(2a2–4a+3)–2a2(3a+4)=6a3–12a2+9a–6a3–8a2=–20a2+9a.原式=–20×(–2)2+9×(–2)
= –20×4–9×2
=–98.方法总结:按运算法则进行化简,然后代入求值,特别注意的是代入“负数”要用括号括起来.单项式乘以多项式的化简求值问题5. 先化简再求值:例5 如果(–3x)2(x2–2nx+2)的展开式中不含x3项,求n的值.方法总结:在整式乘法的混合运算中,要注意运算顺序.注意当要求多项式中不含有哪一项时,则表示这一项的系数为0.解:(–3x)2(x2–2nx+2)=9x2(x2–2nx+2)=9x4–18nx3+18x2.∵展开式中不含x3项,
∴n=0.单项式乘以多项式的化简求字母的值6.如果(x+a)x–2(x+a)的积中不含x项,那么a的值为( )
A.2 B.–2 C.0.5 D.–0.5解析:(x+a)x–2(x+a)=x2+ax–2x–2a
=x2+(a–2)x–2a
∵ x2+(a–2)x–2a中不含x项,
∴ a–2=0,即a=2.
A1. (2018?柳州)计算:(2a)?(ab)=( )
A.2ab B.2a2b
C.3ab D.3a2b?B–4x71.计算 3a2·2a3的结果是( )
A.5a5 B.6a5 C.5a6 D.6a6 2.计算(–9a2b3)·8ab2的结果是( )
A.–72a2b5 B.72a2b5 C.–72a3b5 D.72a3b53.若(ambn)·(a2b)=a5b3 那么m+n=( )
A.8 B.7 C.6 D.5BCD(1)4(a–b+1)=___________________;4a–4b+4(2)3x(2x–y2)=___________________;6x2–3xy2(3)(2x–5y+6z)(–3x) =___________________;–6x2+15xy–18xz(4)(–2a2)2(–a–2b+c)=___________________.–4a5–8a4b+4a4c4.计算5. 计算:–2x2·(xy+y2)–5x(x2y–xy2).解:原式=( –2x2) ·xy+(–2x2) ·y2+(–5x) ·x2y+(–5x) ·(–xy2) = –2x3 y+(–2x2y2)+(–5x3y)+5x2y2 = –7x3 y+3x2y2.6. 解方程:8x(5–x)=34–2x(4x–3). 解得: x=1.解:原式去括号,得:40x–8x2=34–8x2+6x,移项,得: 40x–6x=34,合并同类项,得:34x=34, 如图,一块长方形地用来建造住宅、广场、商厦,求这块地的面积.解:4a[(3a+2b)+(2a–b)]
=4a(5a+b)
=4a·5a+4a·b
= 20a2+4ab.
答:这块地的面积为20a2+4ab. 某同学在计算一个多项式乘以–3x2时,算成了加上–3x2,得到的答案是x2–2x+1,那么正确的计算结果是多少?解:设这个多项式为A,则∴A=4x2–2x+1.∴A·(–3x2)=(4x2–2x+1)(–3x2)A+(–3x2)=x2–2x+1,=–12x4+6x3–3x2.整式乘法单项式乘单项式实质上是转化为同底数幂的运算单项式乘
多项式实质上是转化为单项式×单项式四点注意(1)计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时,同号相乘得正,异号相乘得负
(2)不要出现漏乘现象 (3)运算要有顺序:先乘方,再乘除,最后加减
(4)对于混合运算,注意最后应合并同类项多项式乘多项式 为了把校园建设成为花园式的学 校,经研究决定将原有的长为a米, 宽为b米的足球场向宿舍楼方向加长 m米,向厕所方向加宽n米,扩建成为美化校园绿草地。你是学校的小主人,你能帮助学校计算出扩展后绿地的面积吗?2. 能够运用多项式与多项式的乘法运算法则进行计算.
1. 理解并掌握多项式与多项式的乘法运算法则.1.如何进行单项式与多项式乘法的运算?(2)再把所得的积相加.(1)将单项式分别乘以多项式的各项.2.进行单项式与多项式乘法运算时,要注意什么?(1)不能漏乘:即单项式要乘多项式的每一项.(2)去括号时注意符号的变化.多项式乘多项式的法则回
顾旧知 某地区在退耕还林期间,有一块原长m米,宽为a米的长方形林区,若长增加了n米,宽增加了b米,请你计算这块林区现在的面积.manambnb你能用不同的形式表示所拼图的面积吗?这块林区现在长为(m+n)米,宽为(a+b)米.(m+n)(a+b)m(a+b)+n(a+b)ma+mb+na+nb方法一:方法二:方法三: 由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=ma+ mb+ na+ nb如何进行多项式与多项式相乘的运算?实际上,把(a+b)看成一个整体,有:= ma+mb+na+nb(m+n)(a+b)= m(a+b)+n(a+b) (m+n)X=mX+nX?若X=a+b,如何计算? 多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am1234+an+bm+bn“多乘多” 顺口溜:多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.多项式乘以多项式例1 计算: (1)(3x+1)(x+2); (2)(x–8y)(x–y);解: (1) 原式=3x·x+2·3x+1·x+1×2
=3x2+6x+x+2(2) 原式=x·x–xy–8xy+8y2=3x2+7x+2; =x2–9xy+8y2;用多项式乘以多项式法则进行计算 (3) 原式=x·x2–x·xy+xy2+x2y–xy2+y·y2
=x3–x2y+xy2+x2y–xy2+y3
= x3+y3. 需要注意的几个问题:(1)漏乘;(2)符号问题;(3)最后结果应化成最简形式. (3) (x+y)(x2–xy+y2). 1.快速训练:
(1) (2x+1)(x+3); (2) (m+2n)(m+3n):
(3) ( a – 1)2 ; (4) (a+3b)(a –3b ).
(5) (x+2)(x+3); (6) (x–4)(x+1)
(7) (y+4)(y–2); (8) (y–5)(y–3)a2–9b22x2+7x+3m2+5mn+6n2a2–2a+1x2+5x+6x2–3x–4y2+2y–8y2–8y+15例2 先化简,再求值:(a–2b)(a2+2ab+4b2)–a(a–5b)(a+3b),其中a=–1,b=1.当a=–1,b=1时,解:原式=a3–8b3–(a2–5ab)(a+3b)=a3–8b3–a3–3a2b+5a2b+15ab2=–8b3+2a2b+15ab2.原式=–8+2–15=–21.用多项式乘以多项式法则进行化简求值2.先化简,再求值.
(x–y)(x–2y) – (2x–3y)(x+2y),其中 .?解:(x–y)(x–2y) – (2x–3y)(x+2y)
=x2–2xy–xy+2y2–(2x2+4xy–3xy–6y2) =x2–2xy–xy+2y2–2x2–xy+6y2 = –x2–4xy+8y2当x= –2,y= 时, 原式= –6? 例3 已知ax2+bx+1(a≠0)与3x–2的积不含x2项,也不含x项,求系数a、b的值.解:(ax2+bx+1)(3x–2)=3ax3–2ax2+3bx2–2bx+3x–2,∵积不含x2的项,也不含x的项,方法总结:解决此类问题首先要利用多项式乘法法则计算出展开式,合并同类项后,再根据不含某一项,可得这一项系数等于零,再列出方程解答.
3. 选择题.
(1)计算m2–(m+1)(m–5)的结果正确的是( )
A.–4m–5 B.4m+5
C.m2–4m+5 D.m2+4m–5
(2)(1+x)(2x2+ax+1)的结果中x2项的系数为–2,则a的值为( )
A.–2 B.1
C.–4 D.以上都不对
BC1. (2018?武汉)计算(a–2)(a+3)的结果是( )
A.a2–6 B.a2+a–6
C.a2+6 D.a2–a+6B2. (2018?宁波)在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD–AB=2时,S2–S1的值为( )
A.2a B.2b C.2a–2b D.–2bB2. 如果(x+a)(x+b)的结果中不含x的一次项,那么a、b满足( )
A.a=b B.a=0 C.a=–b D.b=0 C1. 计算(x–1)(x–2)的结果为( )
A.x2+3x–2 B.x2–3x–2
C.x2+3x+2 D.x2–3x+2 D3. (2018?玉林)已知ab=a+b+1,则(a–1)(b–1)=_____ .24. 判别下列解法是否正确,若不正确,请说出理由.漏乘运算法则混淆 5. 计算:(1)(x?3y)(x+7y); (2)(2x + 5y)(3x?2y).+7xy?3yx?=x2 +4xy–21y2; 21y2(2) (2x +5 y)(3x?2y)==x22x?3x ?2x? 2y +5 y? 3x?5y?2y=6x2?4xy+ 15xy?10y2=6x2 +11xy?10y2.6.化简求值:
(4x+3y)(4x–3y)+(2x+y)(3x–5y),其中x=1,y= –2.解:原式=当x=1,y= –2时,
原式=22×1–7×1×(–2)–14×(–2)2=22+14 –56
=–20.解方程与不等式:
1. (x–3)(x–2)+18=(x+9)(x+1);2. (3x+6)(3x–6)<9(x–2)(x+3).解:1. 原式去括号,得:x2–5x+6+18=x2+10x+9,
移项合并,得:15x=15,
解得:x=1;
2.原式去括号,得:9x2–36<9x2+9x–54,
移项合并,得:9x>18,
解得:x>2 . 小东找来一张挂历画包数学课本.已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米,那么小东应在挂历画上裁下一块多大面积的长方形?面积:(2m+2b+c)(2m+a)解:(2m+2b+c)(2m+a)= 4m2+2ma+4bm+2ab+2cm+ca.答:小东应在挂历画上裁下一块
(4m2+2ma+4bm+2ab+2cm+ca)平方厘米的长方形.多项式乘多项式运算法则多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am+an+bm+bn注意不要漏乘;正确确定各项符号;结果要最简. 实质上是转化为单项式乘多项式的运算.(x–1)2在一般情况下不等于x2–12.整式的除法 木星的质量约是1.9×1024吨,地球的质量约是5.98×1021吨,你知道木星的质量约为地球质量的多少倍吗?木星的质量约为地球质量的(1.90×1024)÷(5.98×1021)倍.想一想:上面的式子该如何计算?地球木星1. 掌握同底数幂除法的运算法则并能正确计算. 素养目标2. 知道除0以外任何数的0次幂都等于1.3. 掌握单项式除以单项式及多项式除以单项式的运算法则并能正确计算.同底数幂的除法1.计算:(1)25×23=? (2)x6·x4=?(3)2m×2n=?28x102m+n2.填空:(1)( )( )×23=28 (2)x6·( )( )=x10(3)( )( )×2n=2m+n25x42m本题直接利用同底数幂的乘法法则计算本题逆向利用同底数幂的乘法法则计算相当于求28 ÷23=?相当于求x10÷x6=?相当于求2m+n ÷2n=?4. 试猜想:am ÷an=? (m,n都是正整数,且m>n)3. 观察下面的等式,你能发现什么规律?(1)28 ÷23=25(2)x10÷x6=x4(3) 2m+n ÷2n=2m同底数幂相除,底数不变,指数相减am ÷an=am–n =28–3=x10–6=2(m+n)–n验证:因为am–n ·an=am–n+n=am,所以am ÷an=am–n. 一般地,我们有
am ÷an=am–n (a ≠0,m,n都是正整数,且m>n)
即同底数幂相除,底数不变,指数相减.想一想:am÷am=? (a≠0)答:am÷am=1,根据同底数幂的除法法则可得am÷am=a0.规定a0 =1(a ≠0)这就是说,除0以外任何数的0次幂都等于1.同底数幂的除法例1 计算:
(1)x8 ÷x2 ; (2) (ab)5 ÷(ab)2.解:(1)x8 ÷x2=x8–2=x6; (2) (ab)5 ÷(ab)2=(ab)5–2=(ab)3=a3b3.方法总结:计算同底数幂的除法时,先判断底数是否相同或变形相同,若底数为多项式,可将其看作一个整体,再根据法则计算.同底数幂除法法则的应用1. 计算:
(1)(–xy)13÷(–xy)8; (2)(x–2y)3÷(2y–x)2;
(3)(a2+1)6÷(a2+1)4÷(a2+1)2.(3)原式=(a2+1)6–4–2=(a2+1)0=1.解:(1)原式=(–xy)13–8=(–xy)5=–x5y5;(2)原式=(x–2y)3÷(x–2y)2=x–2y;例2 已知am=12,an=2,a=3,求am–n–1的值.方法总结:解此题的关键是逆用同底数幂的除法,对am–n–1进行变形,再代入数值进行计算.解:∵am=12,an=2,a=3,
∴am–n–1=am÷an÷a=12÷2÷3=2.同底数幂除法法则的逆运用2. (1)已知xa=32,xb=4,求xa–b;解:xa–b=xa ÷ xb=32 ÷ 4=8; (2)已知xm=5,xn=3,求x2m–3n.单项式除以单项式(1)计算:4a2x3·3ab2= ;(2)计算:12a3b2x3 ÷ 3ab2= .12a3b2x3 4a2x3 解法2:原式=4a2x3 · 3ab2 ÷ 3ab2=4a2x3.理解:上面的商式4a2x3的系数4=12 ÷3;a的指数2=3–1,b的指数0=2–2,而b0=1,x的指数3=3–0.解法1: 12a3b2x3 ÷ 3ab2相当于求( )·3ab2=12a3b2x3.
由(1)可知括号里应填4a2x3. 单项式相除, 把系数、同底数的幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连它的指数一起作为商的一个因式. 底数不变,
指数相减.保留在商里
作为因式.单项式除以单项式的法则例3 计算:(1)28x4y2 ÷7x3y;(2)–5a5b3c ÷15a4b.=4xy;(2)原式=(–5÷15)a5–4b3–1c解:(1)原式=(28 ÷7)x4–3y2–1单项式除法以单项式法则的应用 多项式除以单项式要按照法则逐项进行,不得漏项,并且要注意符号的变化.3.下列计算错在哪里?怎样改正?(1)4a8 ÷2a 2= 2a 4 ( ) (2)10a3 ÷5a2=5a ( ) (3)(–9x5) ÷(–3x) =–3x4 ( ) (4)12a3b ÷4a2=3a ( ) 2a62a3x47ab××××系数相除同底数幂的除法,底数不变,指数相减.只在一个被除式里含有的字母,要连同它的指数写在商里,防止遗漏.
求商的系数,应注意符号.4. 计算
(1)(2a2b2c)4z÷(–2ab2c2)2;
(2)(3x3y3z)4÷(3x3y2z)2÷x2y6z.解:(1)原式=16a8b8c4z÷4a2b4c4=4a6b4z;(2)原式=81x12y12z4÷9x6y4z2÷x2y6z=9x4y2z.方法总结:掌握整式的除法的运算法则是解题的关键,在计算过程中注意有乘方的先算乘方,再算乘除.多项式除以单项式 一幅长方形油画的长为(a+b),宽为m,求它的面积.面积为(a+b)m=ma+mb. 若已知油画的面积为(ma+mb),宽为m,如何求它的长?长为(ma+mb)÷m.如何计算(am+bm) ÷m?计算(am+bm) ÷m就相当于求( ) ·m=am+bm,因此不难推断出括里应填a+b.又知am ÷m+bm ÷m=a+b.即 (am+bm) ÷m=am ÷m+bm ÷m 多项式除以单项式,就是用多项式的 除以这个 ,再把所得的商 .单项式每一项相加关键:
应用法则是把多项式除以单项式转化为单项式除以单项式. 多项式除以单项式的法则例4 计算(12a3–6a2+3a) ÷3a.解: (12a3–6a2+3a) ÷3a
=12a3÷3a+(–6a2) ÷3a+3a÷3a
=4a2+(–2a)+1
=4a2–2a+1.方法总结:多项式除以单项式,实质是利用乘法的分配律,将多项式除以单项式问题转化为单项式除以单项式问题来解决.计算过程中,要注意符号问题.多项式除以单项式的法则的应用5.计算:(1)(6x3y4z–4x2y3z+2xy3)÷2xy3;
(2)(72x3y4–36x2y3+9xy2)÷(–9xy2). (2)原式= 72x3y4÷(–9xy2)+(–36x2y3)÷(–9xy2)+9xy2÷(–9xy2)= –8x2y2+4xy–1.解:(1)原式=6x3y4z÷2xy3–4x2y3z÷2xy3+2xy3÷2xy3=3x2yz–2xz+1;例5 先化简,后求值:[2x(x2y–xy2)+xy(xy–x2)]÷x2y,其中x=2015,y=2014.解:原式=[2x3y–2x2y2+x2y2–x3y]÷x2y,原式=x–y=2015–2014=1.=x–y.把x=2015,y=2014代入上式,得多项式除以单项式的化简求值问题6. 求值:(21x4y3–35x3y2+7x2y2)÷(–7x2y),其中x=1,y= –2解:原式=21x4y3 ÷(–7x2y) –35x3y2 ÷(–7x2y) +7x2y2 ÷(–7x2y)= –3x2y2 + 5xy – y把x=1,y=–2代入上式,得?1. (2018?苏州)计算:a4÷a= .2. (2018?达州)已知am=3,an=2,则a2m–n的值为 .?a34.51.下列说法正确的是 ( )
A.(π–3.14)0没有意义
B.任何数的0次幂都等于1
C.(8×106)÷(2×109)=4×103
D.若(x+4)0=1,则x≠–4D 2.下列算式中,不正确的是( )
A.(–12a5b)÷(–3ab)=4a4
B.9xmyn–1÷3xm–2yn–3=3x2y2
C. 4a2b3÷2ab=2ab2
D.x(x–y)2÷(y–x)=x(x–y)D5. 已知一多项式与单项式–7x5y4 的积为21x5y7–28x6y5,则这个多项式是 .–3y3+4xy4.一个长方形的面积为a2+2a,若一边长为a,则另一边长为_____________.a+23.已知28a3bm÷28anb2=b2,那么m,n的取值为( )
A.m=4,n=3 B.m=4,n=1
C.m=1,n=3 D.m=2,n=3 A6.计算: (1)6a3÷2a2; (2)24a2b3÷3ab;
(3)–21a2b3c÷3ab; (4)(14m3–7m2+14m)÷7m.解:(1) 6a3÷2a2
=(6÷2)(a3÷a2)
=3a.(2) 24a2b3÷3ab
=(24÷3)a2–1b3–1
=8ab2.(3)–21a2b3c÷3ab
=(–21÷3)a2–1b3–1c
= –7ab2c;(4)(14m3–7m2+14m)÷7m
=14m3÷7m7m2÷7m+14m÷7m
= 2m2–m+2. 先化简,再求值:(x+y)(x–y)–(4x3y–8xy3)÷2xy,其中x=1,y=–3.解:原式=x2–y2–2x2+4y2原式=–12+3×(–3)2=–1+27=26.当x=1,y=–3时,=–x2+3y2.1. 若32?92x+1÷27x+1=81,求x的值;解:(1)32?34x+2÷33x+3=81, 即 3x+1=34, 解得x=3;3. 已知2x–5y–4=0,求4x÷32y的值.(3)∵2x–5y–4=0,移项,得2x–5y=4.
4x÷32y=22x÷25y=22x–5y=24=16.2. 已知5x=36,5y=2,求5x–2y的值;(2)52y=(5y)2=4,5x–2y=5x÷52y=36÷4=9.整式的除法同底数幂的除法单项式除以单项式 底数不变,指数相减1.系数相除;
2.同底数的幂相除;
3.只在被除式里的因式照搬作为商的一个因式多项式除以单项式转化为单项式除以单项式的问题0指数幂的性质除0以外任何数的0次幂都等于11. 从课后习题中选取;
2. 完成练习册本课时的习题.课后作业
14.1.4 整式的乘法单项式与单项式、多项式相乘1.幂的运算性质有哪几条? 同底数幂的乘法法则:am·an=am+n ( m、n都是正整数).幂的乘方法则:(am)n=amn ( m、n都是正整数).积的乘方法则:(ab)n=anbn ( m、n都是正整数).2.计算:(1)x2 · x3 · x4= ;
(2)(x3)6= ; (3)(–2a4b2)3= ;
(4) (a2)3 · a4= ;
(5) .x9x18–8a12b6a101回
顾旧知1. 掌握单项式与单项式、单项式与多项式相乘的运算法则.2. 能够灵活地进行单项式与单项式、单项式与多项式相乘的运算. 素养目标单项式与单项式相乘 光的速度约是3×105km/s,太阳光照射到地球上需要的时间大约是5×102s,你知道地球与太阳的距离约是多少吗?地球与太阳的距离约是(3×105)×(5×102)km.(3×105)×(5×102)=(3×5)×(105×102)=15×107. 乘法交换律、结合律 同底数幂的乘法这样书写规范吗?不规范,应为1.5×108. 怎样计算(3 ×105)×(5 ×102)?计算过程中用到了哪些运算律及运算性质? 如果将上式中的数字改为字母,比如ac5 ·bc2,怎样计算这个式子?根据以上计算,想一想如何计算单项式乘以单项式? ac5 · bc2 =(a ·b) ·(c5·c2) (乘法交换律、结合律)
=abc5+2 (同底数幂的乘法)
=abc7. 单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.单项式与单项式的乘法法则例1 计算:
(1)(–5a2b)(–3a); (2)(2x)3(–5xy3).解:(1) (–5a2b)(–3a)
= [(–5)×(–3)](a2?a)b
= 15a3b;(2) (2x)3(–5xy3)
=8x3(–5xy3)
=[8×(–5)](x3?x)y3
= –40x4y3.单项式与单项式相乘有理数的乘法与同底数幂的乘法单项式乘以单项式法则的应用1. 在计算时,应先确定积的符号,积的系数等于各因式系数的积;
2. 注意按顺序运算;
3. 不要漏掉只在一个单项式里含有的字母因式;
4. 此性质对三个及以上单项式相乘仍然适用.1.下面各题的计算结果对不对?如果不对,应当怎样改正?
(1)3a3 ·2a2=6a6 ( ) 改正: .
(2) 2x2 ·3x2=6x4 ( ) 改正: .
(3)3x2 ·4x2=12x2 ( ) 改正: .
(4) 5y3·3y5=15y15 ( ) 改正: .3a3 ·2a2=6a5 3x2 ·4x2=12x4 5y3·3y5=15y8 ×××2.计算:(1) 3x2 ·5x3 ; (2)4y ·(–2xy2); (3) (–3x)2 ·4x2 ; (4)(–2a)3(–3a)2.解:(1)原式=(3×5)(x2·x3)=15x5; (2)原式=[4×(–2)](y·y2) ·x= –8xy3; (3) 原式=9x2·4x2 =(9×4)(x2·x2)=36x4; (4)原式= –8a3·9a2 =[(–8)×9](a3·a2)= –72a5单独因式x别漏乘、漏写有乘方运算,先算乘方,再算单项式相乘.例2 已知–2x3m+1y2n与7xn–6y–3–m的积与x4y是同类项,求m2+n的值.解:∵–2x3m+1y2n与7xn–6y–3–m的积与x4y是同类项,∴m2+n=7.方法总结:单项式乘以单项式就是把它们的系数和同底数幂分别相乘,结合同类项的定义,列出二元一次方程组求出参数的值,然后代入求值即可.利用单项式乘法的法则求字母的值3. 已知 求 的值.解得:∴m、n的值分别是m=1,n=2.解:单项式与多项式相乘如图,试求出三块草坪的总面积是多少? 如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____. papcpb 如果把它看成一个大长方形,那么它的边长为________,面积可表示为_________. p(a+b+c)(a+b+c) 如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____. 如果把它看成一个大长方形,那么它的面积可表示为_________. p(a+b+c)pa+pb+pcp(a+b+c)p (a + b+ c)pb+pcpa+根据乘法的分配律 单项式与多项式相乘,就是用单项式乘多项式的每一项,再把所得的积相加.单项式乘以多项式的法则例3 计算:(1)(–4x)·(2x2+3x–1); 解:(1)(–4x)·(2x2+3x–1)==–8x3–12x2+4x;(–4x)·(2x2)(–4x)·3x(–4x)·(–1)++(2)原式单项式与多项式相乘单项式与单项式相乘利用单项式乘以多项式的法则进行运算解题步骤:1.用单项式去乘多项式的每一项,结果是一个多项式,项数与因式中多项式的项数相同.2.含有混合运算的应注意运算顺序,有同类项的必须合并同类项,从而得到最简结果.①②③4.下列各题的解法是否正确,如果错了,指出错在什么地方,并改正过来。×××漏了单独字母漏乘1符号没有变化例4 先化简,再求值:3a(2a2–4a+3)–2a2(3a+4),
其中a=–2.当a=–2时,解:3a(2a2–4a+3)–2a2(3a+4)=6a3–12a2+9a–6a3–8a2=–20a2+9a.原式=–20×(–2)2+9×(–2)
= –20×4–9×2
=–98.方法总结:按运算法则进行化简,然后代入求值,特别注意的是代入“负数”要用括号括起来.单项式乘以多项式的化简求值问题5. 先化简再求值:例5 如果(–3x)2(x2–2nx+2)的展开式中不含x3项,求n的值.方法总结:在整式乘法的混合运算中,要注意运算顺序.注意当要求多项式中不含有哪一项时,则表示这一项的系数为0.解:(–3x)2(x2–2nx+2)=9x2(x2–2nx+2)=9x4–18nx3+18x2.∵展开式中不含x3项,
∴n=0.单项式乘以多项式的化简求字母的值6.如果(x+a)x–2(x+a)的积中不含x项,那么a的值为( )
A.2 B.–2 C.0.5 D.–0.5解析:(x+a)x–2(x+a)=x2+ax–2x–2a
=x2+(a–2)x–2a
∵ x2+(a–2)x–2a中不含x项,
∴ a–2=0,即a=2.
A1. (2018?柳州)计算:(2a)?(ab)=( )
A.2ab B.2a2b
C.3ab D.3a2b?B–4x71.计算 3a2·2a3的结果是( )
A.5a5 B.6a5 C.5a6 D.6a6 2.计算(–9a2b3)·8ab2的结果是( )
A.–72a2b5 B.72a2b5 C.–72a3b5 D.72a3b53.若(ambn)·(a2b)=a5b3 那么m+n=( )
A.8 B.7 C.6 D.5BCD(1)4(a–b+1)=___________________;4a–4b+4(2)3x(2x–y2)=___________________;6x2–3xy2(3)(2x–5y+6z)(–3x) =___________________;–6x2+15xy–18xz(4)(–2a2)2(–a–2b+c)=___________________.–4a5–8a4b+4a4c4.计算5. 计算:–2x2·(xy+y2)–5x(x2y–xy2).解:原式=( –2x2) ·xy+(–2x2) ·y2+(–5x) ·x2y+(–5x) ·(–xy2) = –2x3 y+(–2x2y2)+(–5x3y)+5x2y2 = –7x3 y+3x2y2.6. 解方程:8x(5–x)=34–2x(4x–3). 解得: x=1.解:原式去括号,得:40x–8x2=34–8x2+6x,移项,得: 40x–6x=34,合并同类项,得:34x=34, 如图,一块长方形地用来建造住宅、广场、商厦,求这块地的面积.解:4a[(3a+2b)+(2a–b)]
=4a(5a+b)
=4a·5a+4a·b
= 20a2+4ab.
答:这块地的面积为20a2+4ab. 某同学在计算一个多项式乘以–3x2时,算成了加上–3x2,得到的答案是x2–2x+1,那么正确的计算结果是多少?解:设这个多项式为A,则∴A=4x2–2x+1.∴A·(–3x2)=(4x2–2x+1)(–3x2)A+(–3x2)=x2–2x+1,=–12x4+6x3–3x2.整式乘法单项式乘单项式实质上是转化为同底数幂的运算单项式乘
多项式实质上是转化为单项式×单项式四点注意(1)计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时,同号相乘得正,异号相乘得负
(2)不要出现漏乘现象 (3)运算要有顺序:先乘方,再乘除,最后加减
(4)对于混合运算,注意最后应合并同类项多项式乘多项式 为了把校园建设成为花园式的学 校,经研究决定将原有的长为a米, 宽为b米的足球场向宿舍楼方向加长 m米,向厕所方向加宽n米,扩建成为美化校园绿草地。你是学校的小主人,你能帮助学校计算出扩展后绿地的面积吗?2. 能够运用多项式与多项式的乘法运算法则进行计算.
1. 理解并掌握多项式与多项式的乘法运算法则.1.如何进行单项式与多项式乘法的运算?(2)再把所得的积相加.(1)将单项式分别乘以多项式的各项.2.进行单项式与多项式乘法运算时,要注意什么?(1)不能漏乘:即单项式要乘多项式的每一项.(2)去括号时注意符号的变化.多项式乘多项式的法则回
顾旧知 某地区在退耕还林期间,有一块原长m米,宽为a米的长方形林区,若长增加了n米,宽增加了b米,请你计算这块林区现在的面积.manambnb你能用不同的形式表示所拼图的面积吗?这块林区现在长为(m+n)米,宽为(a+b)米.(m+n)(a+b)m(a+b)+n(a+b)ma+mb+na+nb方法一:方法二:方法三: 由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=ma+ mb+ na+ nb如何进行多项式与多项式相乘的运算?实际上,把(a+b)看成一个整体,有:= ma+mb+na+nb(m+n)(a+b)= m(a+b)+n(a+b) (m+n)X=mX+nX?若X=a+b,如何计算? 多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am1234+an+bm+bn“多乘多” 顺口溜:多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.多项式乘以多项式例1 计算: (1)(3x+1)(x+2); (2)(x–8y)(x–y);解: (1) 原式=3x·x+2·3x+1·x+1×2
=3x2+6x+x+2(2) 原式=x·x–xy–8xy+8y2=3x2+7x+2; =x2–9xy+8y2;用多项式乘以多项式法则进行计算 (3) 原式=x·x2–x·xy+xy2+x2y–xy2+y·y2
=x3–x2y+xy2+x2y–xy2+y3
= x3+y3. 需要注意的几个问题:(1)漏乘;(2)符号问题;(3)最后结果应化成最简形式. (3) (x+y)(x2–xy+y2). 1.快速训练:
(1) (2x+1)(x+3); (2) (m+2n)(m+3n):
(3) ( a – 1)2 ; (4) (a+3b)(a –3b ).
(5) (x+2)(x+3); (6) (x–4)(x+1)
(7) (y+4)(y–2); (8) (y–5)(y–3)a2–9b22x2+7x+3m2+5mn+6n2a2–2a+1x2+5x+6x2–3x–4y2+2y–8y2–8y+15例2 先化简,再求值:(a–2b)(a2+2ab+4b2)–a(a–5b)(a+3b),其中a=–1,b=1.当a=–1,b=1时,解:原式=a3–8b3–(a2–5ab)(a+3b)=a3–8b3–a3–3a2b+5a2b+15ab2=–8b3+2a2b+15ab2.原式=–8+2–15=–21.用多项式乘以多项式法则进行化简求值2.先化简,再求值.
(x–y)(x–2y) – (2x–3y)(x+2y),其中 .?解:(x–y)(x–2y) – (2x–3y)(x+2y)
=x2–2xy–xy+2y2–(2x2+4xy–3xy–6y2) =x2–2xy–xy+2y2–2x2–xy+6y2 = –x2–4xy+8y2当x= –2,y= 时, 原式= –6? 例3 已知ax2+bx+1(a≠0)与3x–2的积不含x2项,也不含x项,求系数a、b的值.解:(ax2+bx+1)(3x–2)=3ax3–2ax2+3bx2–2bx+3x–2,∵积不含x2的项,也不含x的项,方法总结:解决此类问题首先要利用多项式乘法法则计算出展开式,合并同类项后,再根据不含某一项,可得这一项系数等于零,再列出方程解答.
3. 选择题.
(1)计算m2–(m+1)(m–5)的结果正确的是( )
A.–4m–5 B.4m+5
C.m2–4m+5 D.m2+4m–5
(2)(1+x)(2x2+ax+1)的结果中x2项的系数为–2,则a的值为( )
A.–2 B.1
C.–4 D.以上都不对
BC1. (2018?武汉)计算(a–2)(a+3)的结果是( )
A.a2–6 B.a2+a–6
C.a2+6 D.a2–a+6B2. (2018?宁波)在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD–AB=2时,S2–S1的值为( )
A.2a B.2b C.2a–2b D.–2bB2. 如果(x+a)(x+b)的结果中不含x的一次项,那么a、b满足( )
A.a=b B.a=0 C.a=–b D.b=0 C1. 计算(x–1)(x–2)的结果为( )
A.x2+3x–2 B.x2–3x–2
C.x2+3x+2 D.x2–3x+2 D3. (2018?玉林)已知ab=a+b+1,则(a–1)(b–1)=_____ .24. 判别下列解法是否正确,若不正确,请说出理由.漏乘运算法则混淆 5. 计算:(1)(x?3y)(x+7y); (2)(2x + 5y)(3x?2y).+7xy?3yx?=x2 +4xy–21y2; 21y2(2) (2x +5 y)(3x?2y)==x22x?3x ?2x? 2y +5 y? 3x?5y?2y=6x2?4xy+ 15xy?10y2=6x2 +11xy?10y2.6.化简求值:
(4x+3y)(4x–3y)+(2x+y)(3x–5y),其中x=1,y= –2.解:原式=当x=1,y= –2时,
原式=22×1–7×1×(–2)–14×(–2)2=22+14 –56
=–20.解方程与不等式:
1. (x–3)(x–2)+18=(x+9)(x+1);2. (3x+6)(3x–6)<9(x–2)(x+3).解:1. 原式去括号,得:x2–5x+6+18=x2+10x+9,
移项合并,得:15x=15,
解得:x=1;
2.原式去括号,得:9x2–36<9x2+9x–54,
移项合并,得:9x>18,
解得:x>2 . 小东找来一张挂历画包数学课本.已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米,那么小东应在挂历画上裁下一块多大面积的长方形?面积:(2m+2b+c)(2m+a)解:(2m+2b+c)(2m+a)= 4m2+2ma+4bm+2ab+2cm+ca.答:小东应在挂历画上裁下一块
(4m2+2ma+4bm+2ab+2cm+ca)平方厘米的长方形.多项式乘多项式运算法则多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am+an+bm+bn注意不要漏乘;正确确定各项符号;结果要最简. 实质上是转化为单项式乘多项式的运算.(x–1)2在一般情况下不等于x2–12.整式的除法 木星的质量约是1.9×1024吨,地球的质量约是5.98×1021吨,你知道木星的质量约为地球质量的多少倍吗?木星的质量约为地球质量的(1.90×1024)÷(5.98×1021)倍.想一想:上面的式子该如何计算?地球木星1. 掌握同底数幂除法的运算法则并能正确计算. 素养目标2. 知道除0以外任何数的0次幂都等于1.3. 掌握单项式除以单项式及多项式除以单项式的运算法则并能正确计算.同底数幂的除法1.计算:(1)25×23=? (2)x6·x4=?(3)2m×2n=?28x102m+n2.填空:(1)( )( )×23=28 (2)x6·( )( )=x10(3)( )( )×2n=2m+n25x42m本题直接利用同底数幂的乘法法则计算本题逆向利用同底数幂的乘法法则计算相当于求28 ÷23=?相当于求x10÷x6=?相当于求2m+n ÷2n=?4. 试猜想:am ÷an=? (m,n都是正整数,且m>n)3. 观察下面的等式,你能发现什么规律?(1)28 ÷23=25(2)x10÷x6=x4(3) 2m+n ÷2n=2m同底数幂相除,底数不变,指数相减am ÷an=am–n =28–3=x10–6=2(m+n)–n验证:因为am–n ·an=am–n+n=am,所以am ÷an=am–n. 一般地,我们有
am ÷an=am–n (a ≠0,m,n都是正整数,且m>n)
即同底数幂相除,底数不变,指数相减.想一想:am÷am=? (a≠0)答:am÷am=1,根据同底数幂的除法法则可得am÷am=a0.规定a0 =1(a ≠0)这就是说,除0以外任何数的0次幂都等于1.同底数幂的除法例1 计算:
(1)x8 ÷x2 ; (2) (ab)5 ÷(ab)2.解:(1)x8 ÷x2=x8–2=x6; (2) (ab)5 ÷(ab)2=(ab)5–2=(ab)3=a3b3.方法总结:计算同底数幂的除法时,先判断底数是否相同或变形相同,若底数为多项式,可将其看作一个整体,再根据法则计算.同底数幂除法法则的应用1. 计算:
(1)(–xy)13÷(–xy)8; (2)(x–2y)3÷(2y–x)2;
(3)(a2+1)6÷(a2+1)4÷(a2+1)2.(3)原式=(a2+1)6–4–2=(a2+1)0=1.解:(1)原式=(–xy)13–8=(–xy)5=–x5y5;(2)原式=(x–2y)3÷(x–2y)2=x–2y;例2 已知am=12,an=2,a=3,求am–n–1的值.方法总结:解此题的关键是逆用同底数幂的除法,对am–n–1进行变形,再代入数值进行计算.解:∵am=12,an=2,a=3,
∴am–n–1=am÷an÷a=12÷2÷3=2.同底数幂除法法则的逆运用2. (1)已知xa=32,xb=4,求xa–b;解:xa–b=xa ÷ xb=32 ÷ 4=8; (2)已知xm=5,xn=3,求x2m–3n.单项式除以单项式(1)计算:4a2x3·3ab2= ;(2)计算:12a3b2x3 ÷ 3ab2= .12a3b2x3 4a2x3 解法2:原式=4a2x3 · 3ab2 ÷ 3ab2=4a2x3.理解:上面的商式4a2x3的系数4=12 ÷3;a的指数2=3–1,b的指数0=2–2,而b0=1,x的指数3=3–0.解法1: 12a3b2x3 ÷ 3ab2相当于求( )·3ab2=12a3b2x3.
由(1)可知括号里应填4a2x3. 单项式相除, 把系数、同底数的幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连它的指数一起作为商的一个因式. 底数不变,
指数相减.保留在商里
作为因式.单项式除以单项式的法则例3 计算:(1)28x4y2 ÷7x3y;(2)–5a5b3c ÷15a4b.=4xy;(2)原式=(–5÷15)a5–4b3–1c解:(1)原式=(28 ÷7)x4–3y2–1单项式除法以单项式法则的应用 多项式除以单项式要按照法则逐项进行,不得漏项,并且要注意符号的变化.3.下列计算错在哪里?怎样改正?(1)4a8 ÷2a 2= 2a 4 ( ) (2)10a3 ÷5a2=5a ( ) (3)(–9x5) ÷(–3x) =–3x4 ( ) (4)12a3b ÷4a2=3a ( ) 2a62a3x47ab××××系数相除同底数幂的除法,底数不变,指数相减.只在一个被除式里含有的字母,要连同它的指数写在商里,防止遗漏.
求商的系数,应注意符号.4. 计算
(1)(2a2b2c)4z÷(–2ab2c2)2;
(2)(3x3y3z)4÷(3x3y2z)2÷x2y6z.解:(1)原式=16a8b8c4z÷4a2b4c4=4a6b4z;(2)原式=81x12y12z4÷9x6y4z2÷x2y6z=9x4y2z.方法总结:掌握整式的除法的运算法则是解题的关键,在计算过程中注意有乘方的先算乘方,再算乘除.多项式除以单项式 一幅长方形油画的长为(a+b),宽为m,求它的面积.面积为(a+b)m=ma+mb. 若已知油画的面积为(ma+mb),宽为m,如何求它的长?长为(ma+mb)÷m.如何计算(am+bm) ÷m?计算(am+bm) ÷m就相当于求( ) ·m=am+bm,因此不难推断出括里应填a+b.又知am ÷m+bm ÷m=a+b.即 (am+bm) ÷m=am ÷m+bm ÷m 多项式除以单项式,就是用多项式的 除以这个 ,再把所得的商 .单项式每一项相加关键:
应用法则是把多项式除以单项式转化为单项式除以单项式. 多项式除以单项式的法则例4 计算(12a3–6a2+3a) ÷3a.解: (12a3–6a2+3a) ÷3a
=12a3÷3a+(–6a2) ÷3a+3a÷3a
=4a2+(–2a)+1
=4a2–2a+1.方法总结:多项式除以单项式,实质是利用乘法的分配律,将多项式除以单项式问题转化为单项式除以单项式问题来解决.计算过程中,要注意符号问题.多项式除以单项式的法则的应用5.计算:(1)(6x3y4z–4x2y3z+2xy3)÷2xy3;
(2)(72x3y4–36x2y3+9xy2)÷(–9xy2). (2)原式= 72x3y4÷(–9xy2)+(–36x2y3)÷(–9xy2)+9xy2÷(–9xy2)= –8x2y2+4xy–1.解:(1)原式=6x3y4z÷2xy3–4x2y3z÷2xy3+2xy3÷2xy3=3x2yz–2xz+1;例5 先化简,后求值:[2x(x2y–xy2)+xy(xy–x2)]÷x2y,其中x=2015,y=2014.解:原式=[2x3y–2x2y2+x2y2–x3y]÷x2y,原式=x–y=2015–2014=1.=x–y.把x=2015,y=2014代入上式,得多项式除以单项式的化简求值问题6. 求值:(21x4y3–35x3y2+7x2y2)÷(–7x2y),其中x=1,y= –2解:原式=21x4y3 ÷(–7x2y) –35x3y2 ÷(–7x2y) +7x2y2 ÷(–7x2y)= –3x2y2 + 5xy – y把x=1,y=–2代入上式,得?1. (2018?苏州)计算:a4÷a= .2. (2018?达州)已知am=3,an=2,则a2m–n的值为 .?a34.51.下列说法正确的是 ( )
A.(π–3.14)0没有意义
B.任何数的0次幂都等于1
C.(8×106)÷(2×109)=4×103
D.若(x+4)0=1,则x≠–4D 2.下列算式中,不正确的是( )
A.(–12a5b)÷(–3ab)=4a4
B.9xmyn–1÷3xm–2yn–3=3x2y2
C. 4a2b3÷2ab=2ab2
D.x(x–y)2÷(y–x)=x(x–y)D5. 已知一多项式与单项式–7x5y4 的积为21x5y7–28x6y5,则这个多项式是 .–3y3+4xy4.一个长方形的面积为a2+2a,若一边长为a,则另一边长为_____________.a+23.已知28a3bm÷28anb2=b2,那么m,n的取值为( )
A.m=4,n=3 B.m=4,n=1
C.m=1,n=3 D.m=2,n=3 A6.计算: (1)6a3÷2a2; (2)24a2b3÷3ab;
(3)–21a2b3c÷3ab; (4)(14m3–7m2+14m)÷7m.解:(1) 6a3÷2a2
=(6÷2)(a3÷a2)
=3a.(2) 24a2b3÷3ab
=(24÷3)a2–1b3–1
=8ab2.(3)–21a2b3c÷3ab
=(–21÷3)a2–1b3–1c
= –7ab2c;(4)(14m3–7m2+14m)÷7m
=14m3÷7m7m2÷7m+14m÷7m
= 2m2–m+2. 先化简,再求值:(x+y)(x–y)–(4x3y–8xy3)÷2xy,其中x=1,y=–3.解:原式=x2–y2–2x2+4y2原式=–12+3×(–3)2=–1+27=26.当x=1,y=–3时,=–x2+3y2.1. 若32?92x+1÷27x+1=81,求x的值;解:(1)32?34x+2÷33x+3=81, 即 3x+1=34, 解得x=3;3. 已知2x–5y–4=0,求4x÷32y的值.(3)∵2x–5y–4=0,移项,得2x–5y=4.
4x÷32y=22x÷25y=22x–5y=24=16.2. 已知5x=36,5y=2,求5x–2y的值;(2)52y=(5y)2=4,5x–2y=5x÷52y=36÷4=9.整式的除法同底数幂的除法单项式除以单项式 底数不变,指数相减1.系数相除;
2.同底数的幂相除;
3.只在被除式里的因式照搬作为商的一个因式多项式除以单项式转化为单项式除以单项式的问题0指数幂的性质除0以外任何数的0次幂都等于11. 从课后习题中选取;
2. 完成练习册本课时的习题.课后作业
