苏教版五年级上册数学课件: 2.10 多边形的面积 练习四(19张PPT)
文档属性
| 名称 | 苏教版五年级上册数学课件: 2.10 多边形的面积 练习四(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-26 19:30:07 | ||
图片预览


文档简介
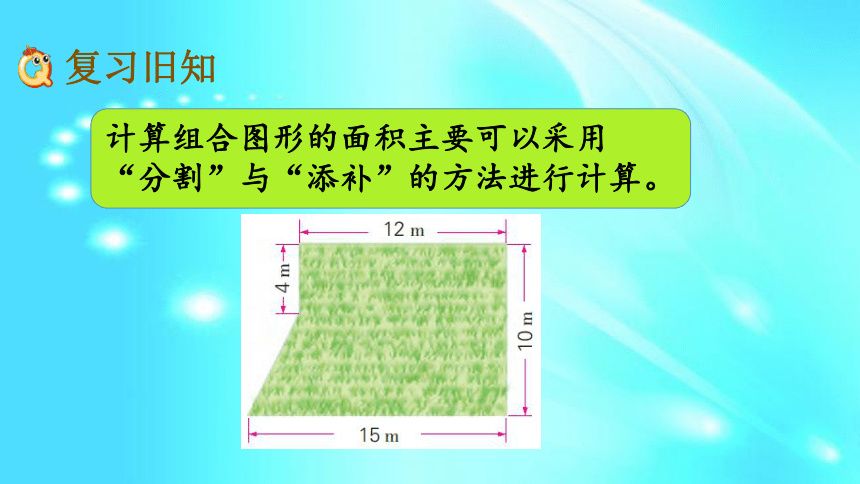
课件19张PPT。练习四复习旧知课堂小结课后作业多边形的面积巩固练习计算组合图形的面积主要可以采用
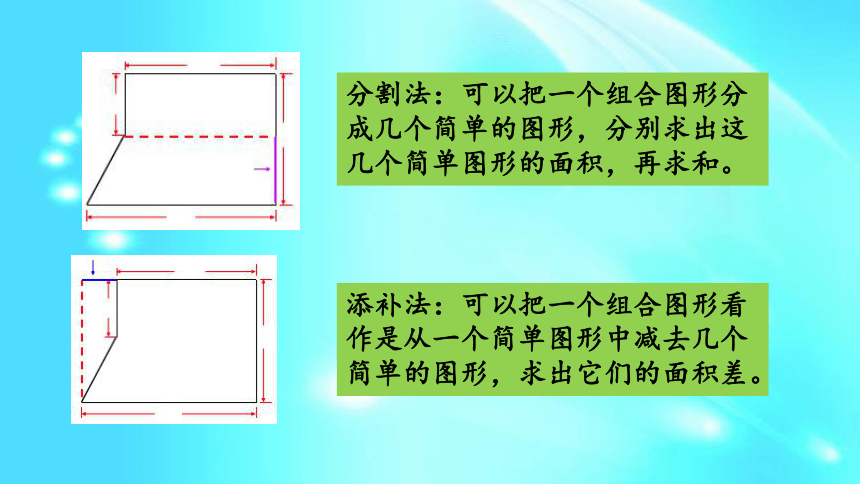
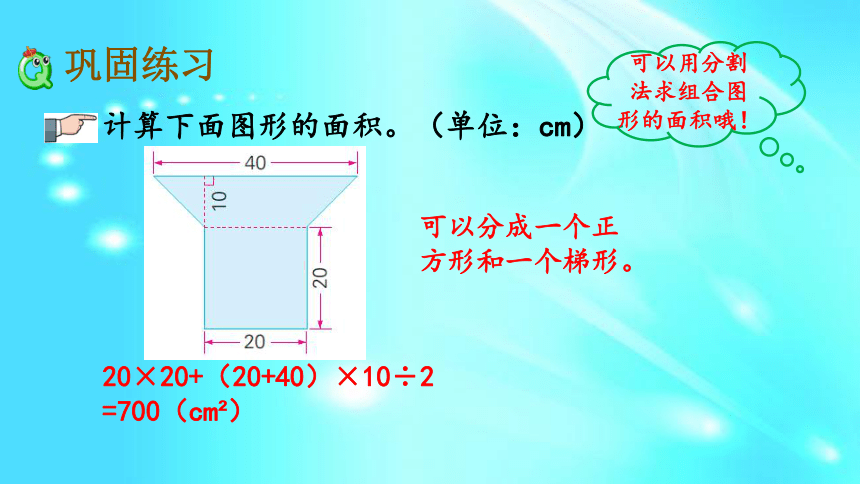
“分割”与“添补”的方法进行计算。b分割法:可以把一个组合图形分成几个简单的图形,分别求出这几个简单图形的面积,再求和。添补法:可以把一个组合图形看作是从一个简单图形中减去几个简单的图形,求出它们的面积差。用数方格的方法计算不规则图形的面积时,先数整格的,再数不满整格的,不满整格的按半格算,计算出的结果是近似值。计算下面图形的面积。(单位:cm)可以用分割法求组合图形的面积哦!可以分成一个正方形和一个梯形。20×20+(20+40)×10÷2
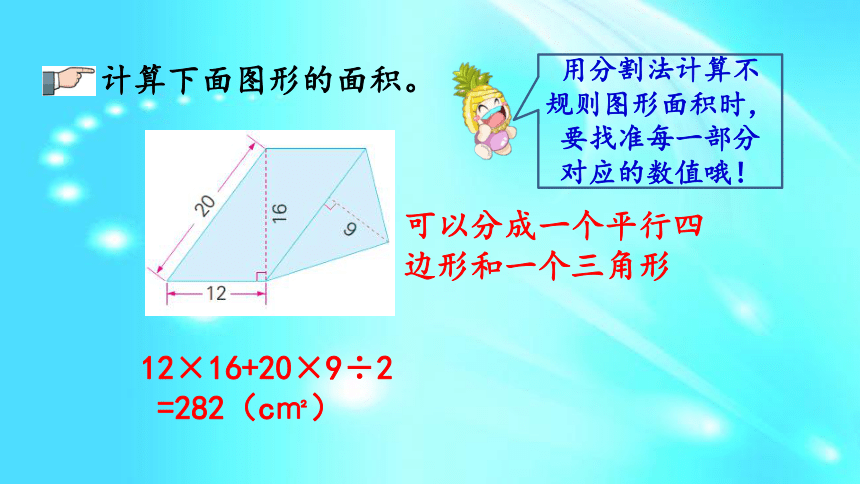
=700(cm2)计算下面图形的面积。用分割法计算不规则图形面积时,要找准每一部分对应的数值哦!可以分成一个平行四边形和一个三角形12×16+20×9÷2
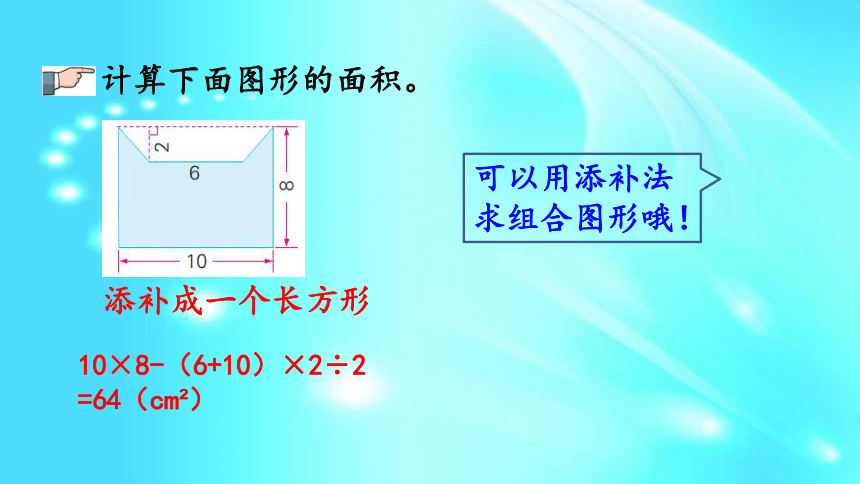
=282(c㎡)可以用添补法求组合图形哦!添补成一个长方形计算下面图形的面积。10×8-(6+10)×2÷2
=64(cm2)绿波小区有一块梯形草坪,草坪的中间有一个长方形的花坛(如下图),草坪的面积是多少平方米?梯形和长方形的面积公式要记牢哦!答:草坪的面积是512平方米。(20+36)×20÷2-12×4=512(平方米)“银苏号”滑翔机模型的尾翼是由两个完全相同的梯形组成的(如下图),它的面积是多少?(4+8)×20÷2×2=240(cm2)答:它的面积是240cm2。找准梯形的上底、下底和高哦!用简便方法计算。 25×17×4 53×28+72×53 540÷45 =25×4×17
=100×17
=1700 =53×(28+72)
=53×100
=5300 =540÷(9×5)
=540÷9÷5
=60÷5
=12一张边长8厘米的正方形纸,从一边的中点到邻边的中点连一条线段。沿这条线段剪去一个角(如下图),剩下的面积是多少?8 8×(8÷2)+(4+8)×4÷2
=56(平方厘米)8÷2=48÷2=488÷2=4答:剩下的面积是56平方厘米。一个牧场的形状如下图。(30+220)×(230-150)÷2+(180+220)×150÷2=40000(平方米)这个牧场的面积是多少平方米?是多少公顷?可以分割成两个梯形来计算牧场的面积哦。答:这个牧场的面积是40000平
方米,是4公顷。40000平方米=4公顷采集一片树叶,把他的轮廓线描在方格纸上,估计它的面积。下面三个大正方形的边长都是32厘米,先计算每个正方形中小方格的面积,再估计荷叶的面积。32÷4=8(厘米)8×8=64(平方厘米)荷叶的面积大约是256~1024平方厘米32÷8=4(厘米)4×4=16(平方厘米)荷叶的面积大约是496~944平方厘米32÷16=2(厘米)2×2=4(平方厘米)荷叶的面积大约是616~824平方厘米在哪个图中估计荷叶面积更接近实际面积?为什么?答:图3估计的荷叶面积更接近实际面积,因为大正方形里的小方格
分得越多,得到的答案越接近实际数。求下面图形的面积。(单位:厘米)8106610×6+4×2÷2
=64(平方厘米)可以将它分割成一个三角形和一个长方形10-6=4(厘米)8-6=2(厘米)这节课你们都学会了哪些知识?在求复杂图形的面积时,可以先把复杂图形通过“割”“补”转化成已学过的图形,再求这些已学过图形面积的和或差。这节课你们都学会了哪些知识?在用数方格的方法计算不规则图形的面积时,不满整格的按半格算,计算出的结果是近似值。这节课你们都学会了哪些知识?有些题目,现有的条件很难与所求的问题直接联系起来,若将题中原有条件与所求问题之间巧用“等量代换”,则可以化难为易。1.从教材课后习题中选取;
2.从课时练中选取。
“分割”与“添补”的方法进行计算。b分割法:可以把一个组合图形分成几个简单的图形,分别求出这几个简单图形的面积,再求和。添补法:可以把一个组合图形看作是从一个简单图形中减去几个简单的图形,求出它们的面积差。用数方格的方法计算不规则图形的面积时,先数整格的,再数不满整格的,不满整格的按半格算,计算出的结果是近似值。计算下面图形的面积。(单位:cm)可以用分割法求组合图形的面积哦!可以分成一个正方形和一个梯形。20×20+(20+40)×10÷2
=700(cm2)计算下面图形的面积。用分割法计算不规则图形面积时,要找准每一部分对应的数值哦!可以分成一个平行四边形和一个三角形12×16+20×9÷2
=282(c㎡)可以用添补法求组合图形哦!添补成一个长方形计算下面图形的面积。10×8-(6+10)×2÷2
=64(cm2)绿波小区有一块梯形草坪,草坪的中间有一个长方形的花坛(如下图),草坪的面积是多少平方米?梯形和长方形的面积公式要记牢哦!答:草坪的面积是512平方米。(20+36)×20÷2-12×4=512(平方米)“银苏号”滑翔机模型的尾翼是由两个完全相同的梯形组成的(如下图),它的面积是多少?(4+8)×20÷2×2=240(cm2)答:它的面积是240cm2。找准梯形的上底、下底和高哦!用简便方法计算。 25×17×4 53×28+72×53 540÷45 =25×4×17
=100×17
=1700 =53×(28+72)
=53×100
=5300 =540÷(9×5)
=540÷9÷5
=60÷5
=12一张边长8厘米的正方形纸,从一边的中点到邻边的中点连一条线段。沿这条线段剪去一个角(如下图),剩下的面积是多少?8 8×(8÷2)+(4+8)×4÷2
=56(平方厘米)8÷2=48÷2=488÷2=4答:剩下的面积是56平方厘米。一个牧场的形状如下图。(30+220)×(230-150)÷2+(180+220)×150÷2=40000(平方米)这个牧场的面积是多少平方米?是多少公顷?可以分割成两个梯形来计算牧场的面积哦。答:这个牧场的面积是40000平
方米,是4公顷。40000平方米=4公顷采集一片树叶,把他的轮廓线描在方格纸上,估计它的面积。下面三个大正方形的边长都是32厘米,先计算每个正方形中小方格的面积,再估计荷叶的面积。32÷4=8(厘米)8×8=64(平方厘米)荷叶的面积大约是256~1024平方厘米32÷8=4(厘米)4×4=16(平方厘米)荷叶的面积大约是496~944平方厘米32÷16=2(厘米)2×2=4(平方厘米)荷叶的面积大约是616~824平方厘米在哪个图中估计荷叶面积更接近实际面积?为什么?答:图3估计的荷叶面积更接近实际面积,因为大正方形里的小方格
分得越多,得到的答案越接近实际数。求下面图形的面积。(单位:厘米)8106610×6+4×2÷2
=64(平方厘米)可以将它分割成一个三角形和一个长方形10-6=4(厘米)8-6=2(厘米)这节课你们都学会了哪些知识?在求复杂图形的面积时,可以先把复杂图形通过“割”“补”转化成已学过的图形,再求这些已学过图形面积的和或差。这节课你们都学会了哪些知识?在用数方格的方法计算不规则图形的面积时,不满整格的按半格算,计算出的结果是近似值。这节课你们都学会了哪些知识?有些题目,现有的条件很难与所求的问题直接联系起来,若将题中原有条件与所求问题之间巧用“等量代换”,则可以化难为易。1.从教材课后习题中选取;
2.从课时练中选取。
