西师大版六年级上册数学课件:2.11解决问题(16张PPT)
文档属性
| 名称 | 西师大版六年级上册数学课件:2.11解决问题(16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-28 07:42:01 | ||
图片预览




文档简介
课件16张PPT。解决问题课前导入探究新知课堂小结课后作业圆课堂练习你会求圆环的面积吗?环形的面积等于外圆面积减去内圆面积。用S表示环形的面积,环形的面积公式是
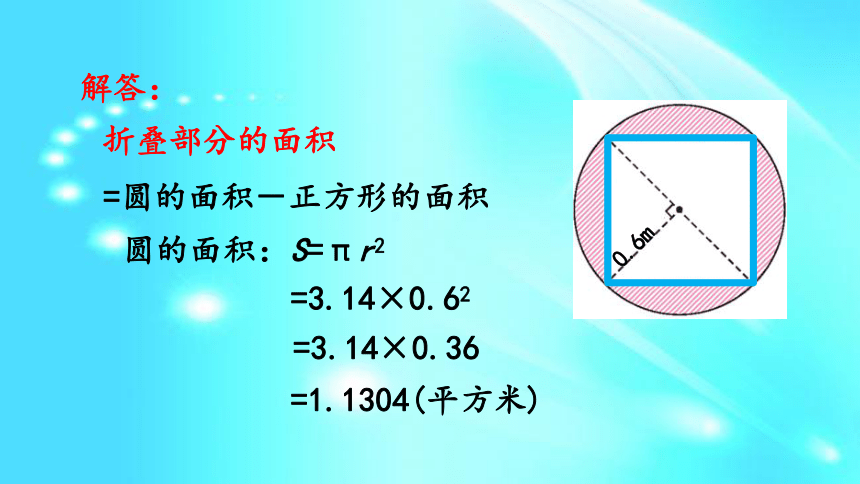
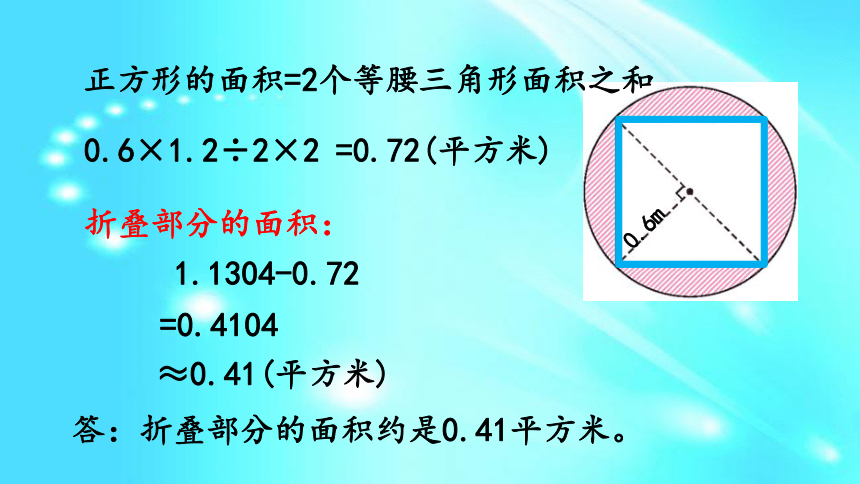
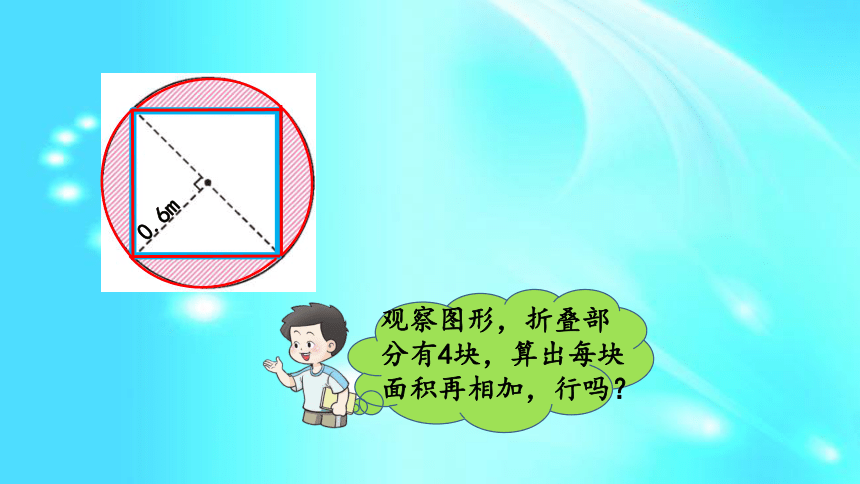
S=πR2-πr2或S=π(R2-r2)。课前导入Rr环宽一张可折叠的圆桌,半径是0.6米,折叠后成了正方形。折叠部分的面积约是多少平方米?(得数保留两位小数)例 6 0.6m探究新知0.6m折叠部分的面积=圆的面积-正方形的面积圆的面积:S=πr2解答:=3.14×0.62=3.14×0.36=1.1304(平方米)折叠部分的面积:答:折叠部分的面积约是0.41平方米。0.6m0.6×1.2÷2×2=0.72(平方米)1.1304-0.72=0.4104≈0.41(平方米)正方形的面积=2个等腰三角形面积之和观察图形,折叠部分有4块,算出每块面积再相加,行吗?0.6m求圆形花坛周围小路的面积:花坛周围的小路正好2米宽。花坛的半径是8米。花坛周围小路的面积 = 外圆面积 - 内圆面积由题意可得:解:花坛外圆的面积:花坛内圆的面积:花坛小路的面积:答:花坛周围的小路的面积是113.04 ㎡。3.14×(8+2)2 =314(㎡)3.14 ×82 =200.96(㎡)314-200.96=113.04(㎡)计算下面涂色部分的面积。(单位:米)解:答:涂色部分的面积是103.62平方米。 涂色部分面积
=外圆面积-内圆面积473.14×(72-42)=3.14×33=103.62(平方米)有一个运动场,两端是半圆,中间是长方形。它的周长和面积各是多少?解:100米64米左右两个半圆刚好能组成一个圆。周长=长方形两条长+圆的周长C=100×2+3.14×64=400.96(米) 有一个运动场,两端是半圆,中间是长方形。它的周长和面积各是多少?解:100米64米左右两个半圆刚好能组成一个圆。面积=长方形面积+圆的面积100×64+3.14×(64÷2)2=9615.36(平方米) =6400+3.14×1024=6400+3215.36求阴影部分的面积。圆的面积合起来就是一个整圆?2cm2cm2cm现在你能独立完成这道题了吗?解题思路:求阴影部分的面积。2cm2cm2cm解:答:阴影部分的面积是50.24cm2。S=πr2=3.14×42=3.14×16=50.24(cm2)这节课你们都学会了哪些知识?课堂小结会用“切割法”“平移法”等方法求组合图形的面积。能够运用“转化法”把无法找出已知条件的问题,换个角度思考,把未知条件转化成已知条件来解决。 1.从教材课后习题中选取;
2.从课时练中选取。课后作业
S=πR2-πr2或S=π(R2-r2)。课前导入Rr环宽一张可折叠的圆桌,半径是0.6米,折叠后成了正方形。折叠部分的面积约是多少平方米?(得数保留两位小数)例 6 0.6m探究新知0.6m折叠部分的面积=圆的面积-正方形的面积圆的面积:S=πr2解答:=3.14×0.62=3.14×0.36=1.1304(平方米)折叠部分的面积:答:折叠部分的面积约是0.41平方米。0.6m0.6×1.2÷2×2=0.72(平方米)1.1304-0.72=0.4104≈0.41(平方米)正方形的面积=2个等腰三角形面积之和观察图形,折叠部分有4块,算出每块面积再相加,行吗?0.6m求圆形花坛周围小路的面积:花坛周围的小路正好2米宽。花坛的半径是8米。花坛周围小路的面积 = 外圆面积 - 内圆面积由题意可得:解:花坛外圆的面积:花坛内圆的面积:花坛小路的面积:答:花坛周围的小路的面积是113.04 ㎡。3.14×(8+2)2 =314(㎡)3.14 ×82 =200.96(㎡)314-200.96=113.04(㎡)计算下面涂色部分的面积。(单位:米)解:答:涂色部分的面积是103.62平方米。 涂色部分面积
=外圆面积-内圆面积473.14×(72-42)=3.14×33=103.62(平方米)有一个运动场,两端是半圆,中间是长方形。它的周长和面积各是多少?解:100米64米左右两个半圆刚好能组成一个圆。周长=长方形两条长+圆的周长C=100×2+3.14×64=400.96(米) 有一个运动场,两端是半圆,中间是长方形。它的周长和面积各是多少?解:100米64米左右两个半圆刚好能组成一个圆。面积=长方形面积+圆的面积100×64+3.14×(64÷2)2=9615.36(平方米) =6400+3.14×1024=6400+3215.36求阴影部分的面积。圆的面积合起来就是一个整圆?2cm2cm2cm现在你能独立完成这道题了吗?解题思路:求阴影部分的面积。2cm2cm2cm解:答:阴影部分的面积是50.24cm2。S=πr2=3.14×42=3.14×16=50.24(cm2)这节课你们都学会了哪些知识?课堂小结会用“切割法”“平移法”等方法求组合图形的面积。能够运用“转化法”把无法找出已知条件的问题,换个角度思考,把未知条件转化成已知条件来解决。 1.从教材课后习题中选取;
2.从课时练中选取。课后作业
