(复习公开课)函数图像的作法与应用解题策略 课件(35张PPT)
文档属性
| 名称 | (复习公开课)函数图像的作法与应用解题策略 课件(35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-27 18:11:44 | ||
图片预览




文档简介
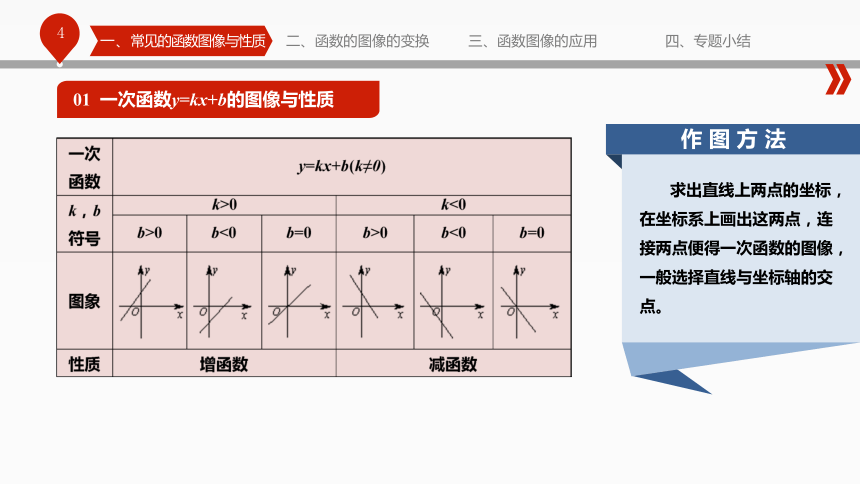
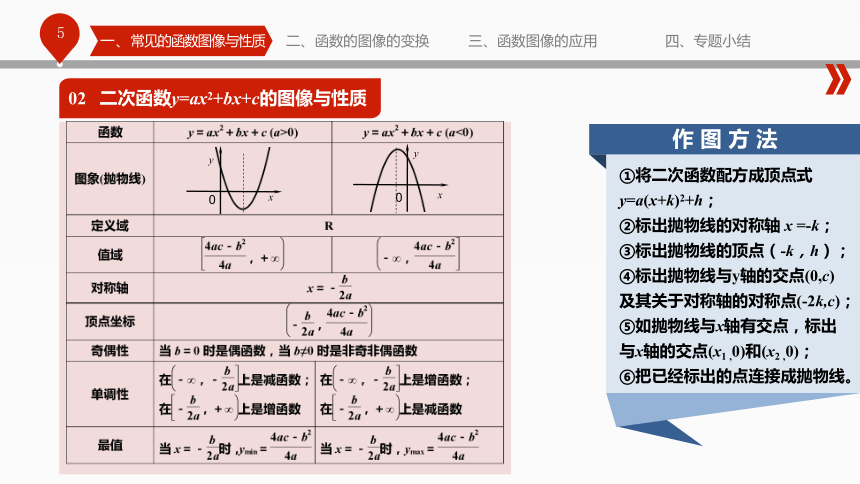
课件35张PPT。设计与主讲:李 君高考数学重难点突破——函数图像的作法与应用Contents Page目录页— * — 一二三四常见函数的图像与性质 函数图像的变换函数图像的应用专题小结常见函数的图像与性质01 一次函数y=kx+b的图像与性质02 二次函数y=ax2+bx+c的图像与性质03 反比例函数y=k/x的图像与性质04 指数函数y=ax的图像与性质05 对数函数y=logax的图像与性质06 幂函数y=xa的图像与性质07 几类特殊函数的图像与性质四、专题小结一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用01 一次函数y=kx+b的图像与性质 求出直线上两点的坐标,在坐标系上画出这两点,连接两点便得一次函数的图像, 一般选择直线与坐标轴的交点。02 二次函数y=ax2+bx+c的图像与性质一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结①将二次函数配方成顶点式y=a(x+k)2+h;
②标出抛物线的对称轴 x =-k;
③标出抛物线的顶点(-k,h);
④标出抛物线与y轴的交点(0,c)及其关于对称轴的对称点(-2k,c);
⑤如抛物线与x轴有交点,标出与x轴的交点(x1 ,0)和(x2 ,0);
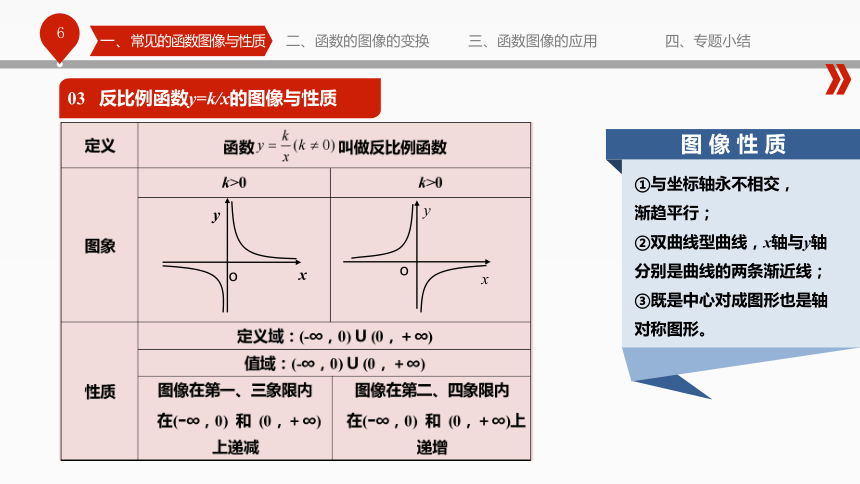
⑥把已经标出的点连接成抛物线。03 反比例函数y=k/x的图像与性质①与坐标轴永不相交,
渐趋平行;
②双曲线型曲线,x轴与y轴
分别是曲线的两条渐近线;
③既是中心对成图形也是轴
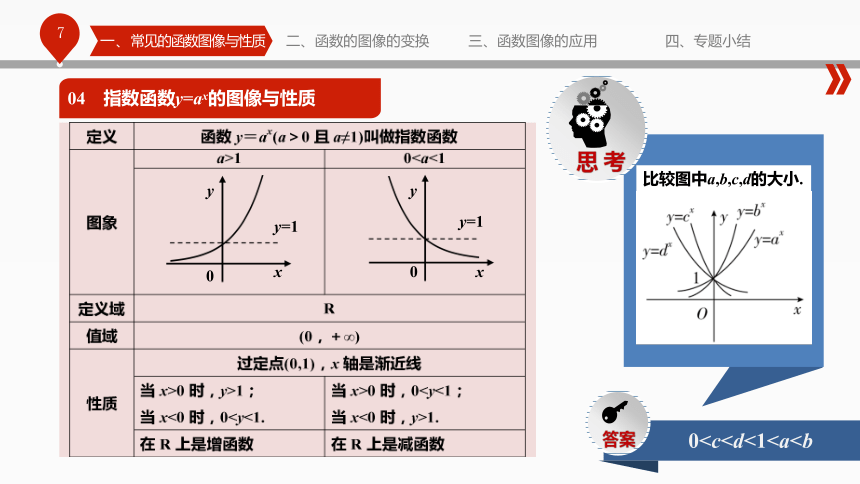
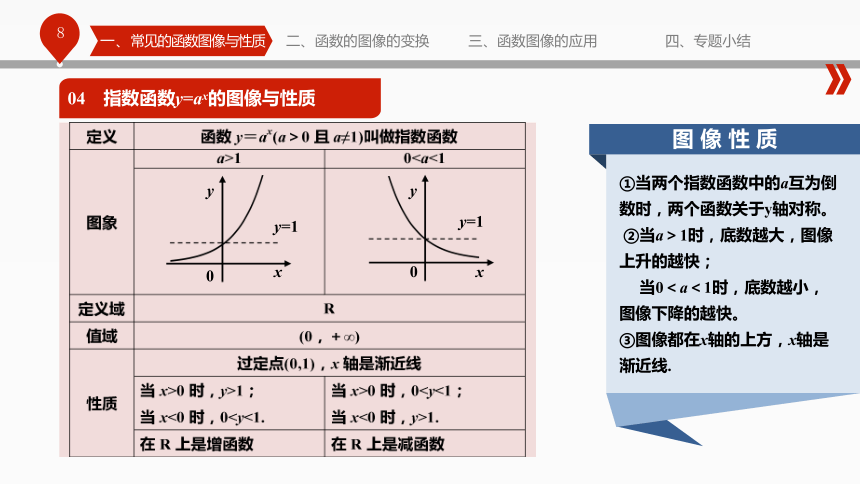
对称图形。一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结04 指数函数y=ax的图像与性质0 ②当a>1时,底数越大,图像上升的越快;
当0<a<1时,底数越小,图像下降的越快。
③图像都在x轴的上方,x轴是渐近线.
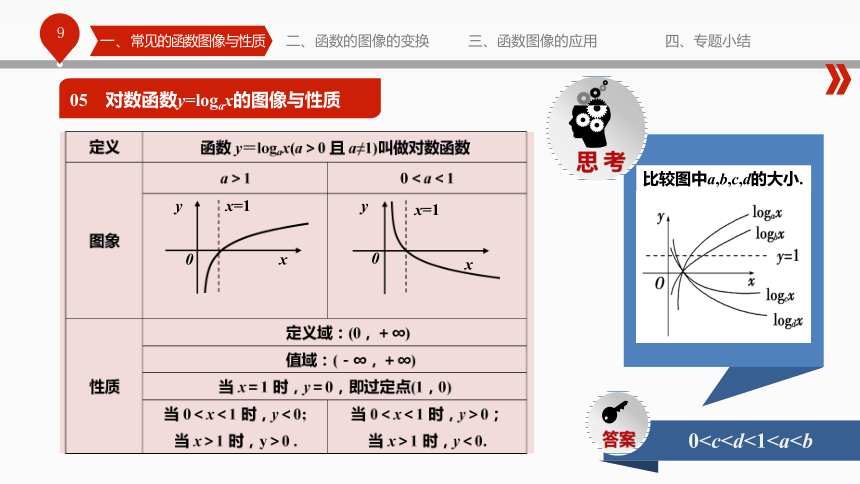
一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结05 对数函数y=logax的图像与性质一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结0 ②当a>1时,底数越大,图像上升的越慢;
当0<a<1时,底数越小,图像下降的越快.
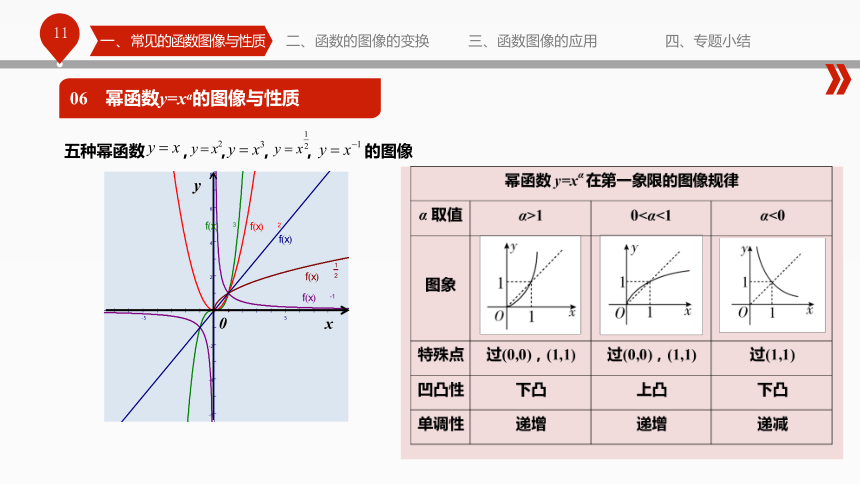
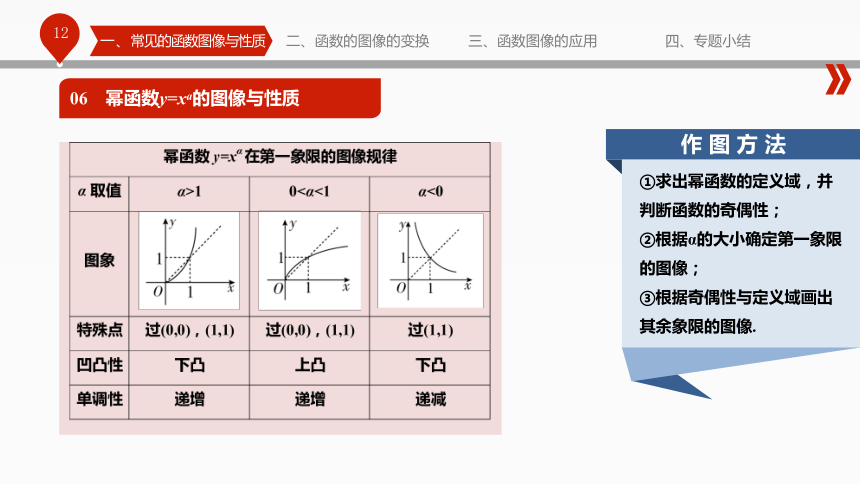
③图像都在y轴的右方,y轴是渐近线. 五种幂函数 , , , , 的图像06 幂函数y=xa的图像与性质一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结06 幂函数y=xa的图像与性质一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结①求出幂函数的定义域,并
判断函数的奇偶性;
②根据α的大小确定第一象限
的图像;
③根据奇偶性与定义域画出
其余象限的图像.②函数 的图像与性质 06 幂函数y=xa的图像与性质一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结函数 的图像 函数 的图像 对称轴x=a顶点(a,b)平移06 幂函数y=xa的图像与性质07 几类特殊函数的图像与性质函数图像的变换y=-f(-x)02 对称变换y=-f(x)y=f(-x)y=logax四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用03 翻折变换f(|x|)|f(x)|四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用04 伸缩变换y=f(ax)y=Af(x)四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用y=f(x)y=f(x)y=f(x)y=f(x)y=f(2x)y=1.5f(x)常用结论四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用(1)函数y=f(x)与y=f(2a-x)的图象关于直线x=a对称.
(2)函数y=f(x)与y=2b-f(2a-x)的图象关于点(a,b)中心对称.
(3)若函数y=f(x)对定义域内任意自变量x满足f(a+x)=f(a-x)或 者f(x)=f(2a-x),则函数
y=f(x)的图象关于直线x=a对称.y=f(x)y=f(2a-x)对称轴x=a对称中心
(a,b)y=f(x)y=2b-f(2a-x)对称轴x=ay=f(x)函数图像的应用三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换(2)画出y=f(x)的图像,再作其关于y轴对称的图像,得到y=f(-x)的图像,
再将所得的图像向右平移1个单位,得到y=f[-(x-1)]=f(-x+1)的图像。CC三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、作图像的图像(1)函数f(x)=ln(x2+1)的图象大致是( )AB(1)∵f(-x)=ln[(-x)2+1]=ln(x2+1)=f(x),
∴f(x)是偶函数,排除C.
∵x2+1≥1,则ln(x2+1)≥0,
且当x=0时 f(0)=0, 所以排除B,D,选A.四、专题小结 一、常见的函数图像与性质二、函数的图像的变换CA三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换②③D三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换(1)[2015·北京高考]如图,函数f(x)的图象为折线ACB,则不
等式 f(x)≥log2(x+1)的解集是( )
A.{x|-1 B.{x|-1≤x≤1}
C.{x|-1 D.{x|-1 ∴a≥-1 .Ca≥-1三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换5(2)[2015·湖南高考]若函数f(x)=|2x-2|-b有两个零点,
则实数b的取值范围是________.(2)由f(x)=|2x-2|-b=0
得|2x-2|=b.
画出y=|2x-2|与y=b的图象,则当0两个交点,f(x)=|2x-2|-b有
两个零点.(0,2)三、函数图像的应用四、专题总结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用函数图像的变换注意在判断平移的方向和长度时要保证x前面的系数是“1”。函数图像的识别四、专题总结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用研究不等式的解研究函数的性质Thank You
②标出抛物线的对称轴 x =-k;
③标出抛物线的顶点(-k,h);
④标出抛物线与y轴的交点(0,c)及其关于对称轴的对称点(-2k,c);
⑤如抛物线与x轴有交点,标出与x轴的交点(x1 ,0)和(x2 ,0);
⑥把已经标出的点连接成抛物线。03 反比例函数y=k/x的图像与性质①与坐标轴永不相交,
渐趋平行;
②双曲线型曲线,x轴与y轴
分别是曲线的两条渐近线;
③既是中心对成图形也是轴
对称图形。一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结04 指数函数y=ax的图像与性质0
当0<a<1时,底数越小,图像下降的越快。
③图像都在x轴的上方,x轴是渐近线.
一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结05 对数函数y=logax的图像与性质一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结0
当0<a<1时,底数越小,图像下降的越快.
③图像都在y轴的右方,y轴是渐近线. 五种幂函数 , , , , 的图像06 幂函数y=xa的图像与性质一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结06 幂函数y=xa的图像与性质一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结①求出幂函数的定义域,并
判断函数的奇偶性;
②根据α的大小确定第一象限
的图像;
③根据奇偶性与定义域画出
其余象限的图像.②函数 的图像与性质 06 幂函数y=xa的图像与性质一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结函数 的图像 函数 的图像 对称轴x=a顶点(a,b)平移06 幂函数y=xa的图像与性质07 几类特殊函数的图像与性质函数图像的变换y=-f(-x)02 对称变换y=-f(x)y=f(-x)y=logax四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用03 翻折变换f(|x|)|f(x)|四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用04 伸缩变换y=f(ax)y=Af(x)四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用y=f(x)y=f(x)y=f(x)y=f(x)y=f(2x)y=1.5f(x)常用结论四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用(1)函数y=f(x)与y=f(2a-x)的图象关于直线x=a对称.
(2)函数y=f(x)与y=2b-f(2a-x)的图象关于点(a,b)中心对称.
(3)若函数y=f(x)对定义域内任意自变量x满足f(a+x)=f(a-x)或 者f(x)=f(2a-x),则函数
y=f(x)的图象关于直线x=a对称.y=f(x)y=f(2a-x)对称轴x=a对称中心
(a,b)y=f(x)y=2b-f(2a-x)对称轴x=ay=f(x)函数图像的应用三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换(2)画出y=f(x)的图像,再作其关于y轴对称的图像,得到y=f(-x)的图像,
再将所得的图像向右平移1个单位,得到y=f[-(x-1)]=f(-x+1)的图像。CC三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换三、作图像的图像(1)函数f(x)=ln(x2+1)的图象大致是( )AB(1)∵f(-x)=ln[(-x)2+1]=ln(x2+1)=f(x),
∴f(x)是偶函数,排除C.
∵x2+1≥1,则ln(x2+1)≥0,
且当x=0时 f(0)=0, 所以排除B,D,选A.四、专题小结 一、常见的函数图像与性质二、函数的图像的变换CA三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换②③D三、函数图像的应用四、专题小结 一、常见的函数图像与性质二、函数的图像的变换(1)[2015·北京高考]如图,函数f(x)的图象为折线ACB,则不
等式 f(x)≥log2(x+1)的解集是( )
A.{x|-1
C.{x|-1
则实数b的取值范围是________.(2)由f(x)=|2x-2|-b=0
得|2x-2|=b.
画出y=|2x-2|与y=b的图象,则当0
两个零点.(0,2)三、函数图像的应用四、专题总结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用函数图像的变换注意在判断平移的方向和长度时要保证x前面的系数是“1”。函数图像的识别四、专题总结 一、常见的函数图像与性质二、函数的图像的变换三、函数图像的应用研究不等式的解研究函数的性质Thank You
