2019年高考物理备考:微元法在电磁感应问题中的应用 17张PPT
文档属性
| 名称 | 2019年高考物理备考:微元法在电磁感应问题中的应用 17张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 330.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-05-27 00:00:00 | ||
图片预览


文档简介
2019年高考物理备考
——微元法在电磁感应问题中的应用
2008.12.16
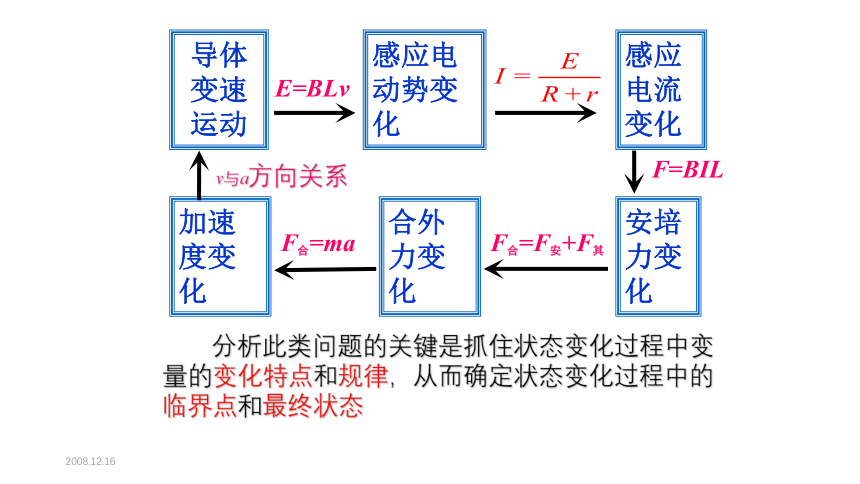
加速度变化
合外力变化
安培力变化
F=BIL
v与a方向关系
F合=ma
导体
变速运动
感应电动势变化
E=BLv
感应电流变化
F合=F安+F其
分析此类问题的关键是抓住状态变化过程中变量的变化特点和规律,从而确定状态变化过程中的临界点和最终状态
2008.12.16
v
t
v0
v0
B
R
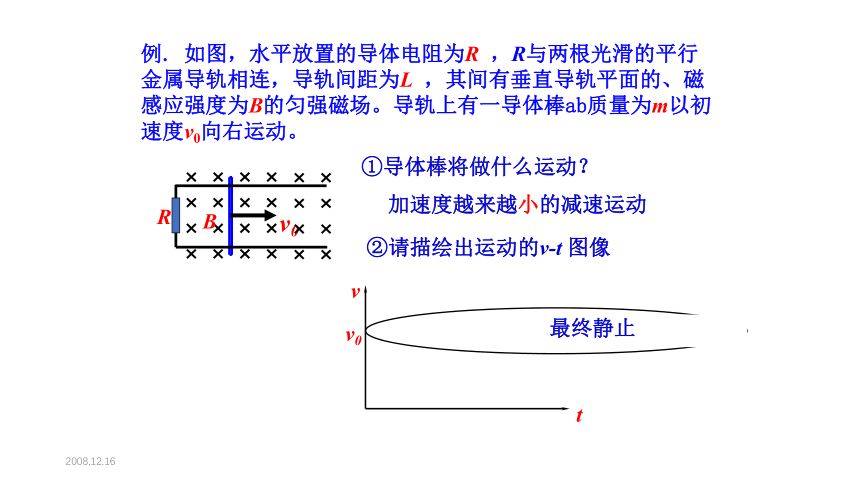
例. 如图,水平放置的导体电阻为R ,R与两根光滑的平行金属导轨相连,导轨间距为L ,其间有垂直导轨平面的、磁感应强度为B的匀强磁场。导轨上有一导体棒ab质量为m以初速度v0向右运动。
①导体棒将做什么运动?
加速度越来越小的减速运动
②请描绘出运动的v-t 图像
最终静止
2008.12.16
v
t
v0
v
B
R
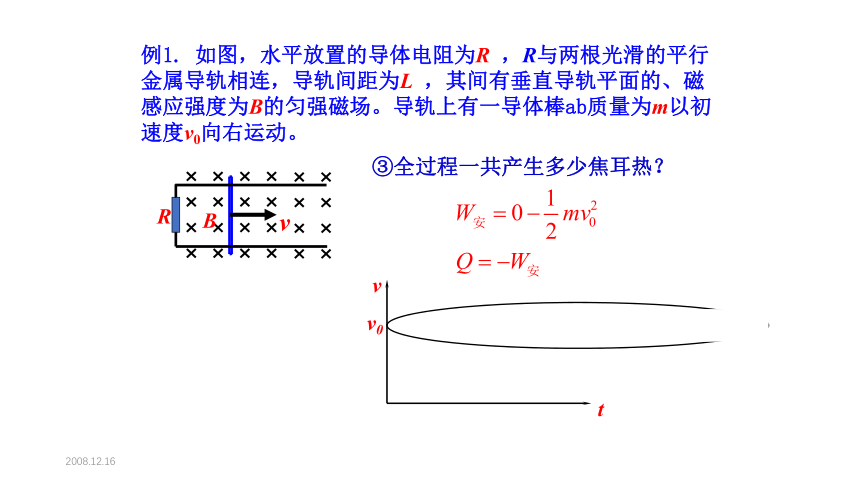
例1. 如图,水平放置的导体电阻为R ,R与两根光滑的平行金属导轨相连,导轨间距为L ,其间有垂直导轨平面的、磁感应强度为B的匀强磁场。导轨上有一导体棒ab质量为m以初速度v0向右运动。
③全过程一共产生多少焦耳热?
2008.12.16
v
t
v
B
R
例1. 如图,水平放置的导体电阻为R ,R与两根光滑的平行金属导轨相连,导轨间距为L ,其间有垂直导轨平面的、磁感应强度为B的匀强磁场。导轨上有一导体棒ab质量为m以初速度v0向右运动。
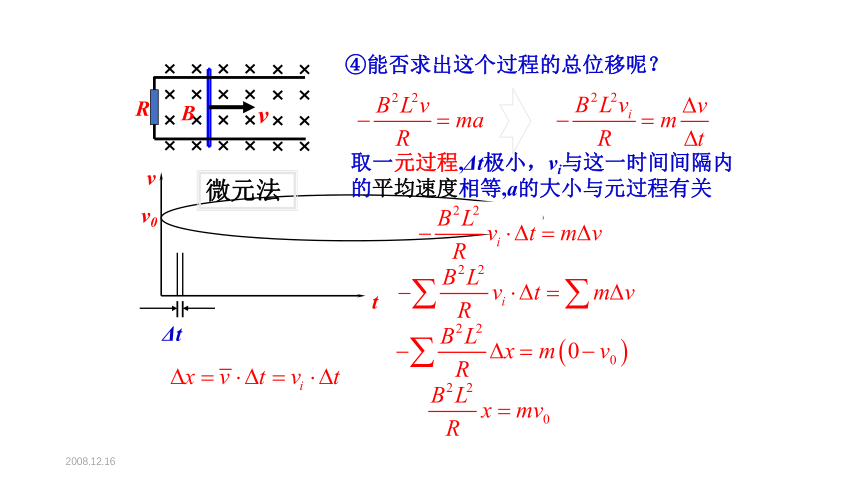
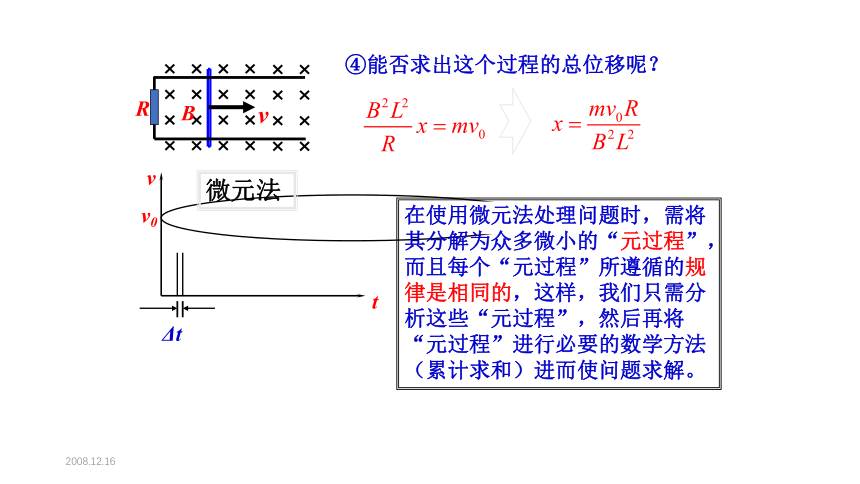
④能否求出这个过程的总位移呢?
位移:图像与横轴所包含的面积
运动规律(牛顿第二定律):
即:
v0
2008.12.16
v
t
v
B
R
④能否求出这个过程的总位移呢?
微元法
Δt
取一元过程,Δt极小,vi与这一时间间隔内的平均速度相等,a的大小与元过程有关
v0
2008.12.16
v
t
v
B
R
④能否求出这个过程的总位移呢?
微元法
Δt
在使用微元法处理问题时,需将其分解为众多微小的“元过程”,而且每个“元过程”所遵循的规律是相同的,这样,我们只需分析这些“元过程”,然后再将“元过程”进行必要的数学方法(累计求和)进而使问题求解。
v0
2008.12.16
v
t
v
B
R
④能否求出这个过程的总位移呢?
⑤能否求出全过程中通过导体某个横截面的电量?
v0
2008.12.16
v
t
v
B
R
④能否求出这个过程的总位移呢?
⑤能否求出全过程中通过导体某个横截面的电量?
微元法
Δt
I
2008.12.16
F
B
R
引申1: 如图,水平放置的导体电阻为R ,R与两根光滑的平行金属导轨相连,导轨间距为L ,其间有垂直导轨平面的、磁感应强度为B的匀强磁场。导轨上有一导体棒ab质量为m受到大小为F的恒力作用从静止开始向右运动。
①导体棒将做什么运动?
加速度越来越小的加速运动,
②请描绘出运动的v-t 图像
最终做匀速运动,外力F与安培力平衡
v
t
2008.12.16
F
B
R
v
t
③末速度多大?
vm
t0
④若在t时刻,棒作匀速运动,求这段时间内的总位移。(t > t0)
t
Δt
运动规律
思考:求该过程中产生的焦耳热
2008.12.16
引申2:如图,竖直放置的光滑U形导轨宽为L,上端串有一个电容,电容为C,磁感应强度为B的匀强磁场方向垂直于纸面向里。金属棒ab的质量为m,与导轨接触良好,不计摩擦及各部分电阻,试通过计算说明金属棒的运动情况。
a
b
C
要说明运动情况,可能有哪些?
匀速,匀加速还是变加速?
找出F-t,或 a-t 的关系
需要通过计算说明什么问题?
2008.12.16
a
b
C
mg
BIL
运动规律
这种情况下,欧姆定律适用么?
恒量
即物体作匀加速直线运动!
分析元过程来帮助理解运动细节
微元
分析受力
不适用
2008.12.16
小结——微元法在电磁感应问题中的应用
在处理问题时,从对事物的极小部分(微元)分析入手,达到解决事物整体的方法。
在使用微元法处理问题时,需将其分解为众多微小的“元过程”,而且每个“元过程”所遵循的规律是相同的,这样,我们只需分析这些“元过程”,然后再将“元过程”进行必要的数学方法(累计求和)进而使问题求解。
在电磁感应问题中,常常遇到非匀变速运动过程中求位移,电量,能量等问题,灵活运用微元的思想,可以帮助我们更深刻的理解物理过程。
2008.12.16
思考题
d
d
d
d
d
d
d
P
O
N
M
v0
如图,空间等间距分布着水平方向的条形匀强磁场, 竖直方向磁场区域足够长, 磁感应强度为B=1T ,每一条形磁场区域的宽度及相邻条形磁场区域的间距均为d=0.5m,现有一边长l=0.2m、质量m=0.1kg、电阻R=0.1Ω的正方形线框MNOP以v0=7m/s的初速从左侧磁场边缘水平进入磁场
求①线框从开始进入磁场到竖直
下落的过程中产生的焦耳热Q
2008.12.16
②线框能穿过的完整条形磁场
区域的个数n。
d
d
d
d
d
d
d
P
O
N
M
v0
B、d、m、l、R、v0
微元法
∴能完整的穿过4个条形磁场区域
谢谢!
——微元法在电磁感应问题中的应用
2008.12.16
加速度变化
合外力变化
安培力变化
F=BIL
v与a方向关系
F合=ma
导体
变速运动
感应电动势变化
E=BLv
感应电流变化
F合=F安+F其
分析此类问题的关键是抓住状态变化过程中变量的变化特点和规律,从而确定状态变化过程中的临界点和最终状态
2008.12.16
v
t
v0
v0
B
R
例. 如图,水平放置的导体电阻为R ,R与两根光滑的平行金属导轨相连,导轨间距为L ,其间有垂直导轨平面的、磁感应强度为B的匀强磁场。导轨上有一导体棒ab质量为m以初速度v0向右运动。
①导体棒将做什么运动?
加速度越来越小的减速运动
②请描绘出运动的v-t 图像
最终静止
2008.12.16
v
t
v0
v
B
R
例1. 如图,水平放置的导体电阻为R ,R与两根光滑的平行金属导轨相连,导轨间距为L ,其间有垂直导轨平面的、磁感应强度为B的匀强磁场。导轨上有一导体棒ab质量为m以初速度v0向右运动。
③全过程一共产生多少焦耳热?
2008.12.16
v
t
v
B
R
例1. 如图,水平放置的导体电阻为R ,R与两根光滑的平行金属导轨相连,导轨间距为L ,其间有垂直导轨平面的、磁感应强度为B的匀强磁场。导轨上有一导体棒ab质量为m以初速度v0向右运动。
④能否求出这个过程的总位移呢?
位移:图像与横轴所包含的面积
运动规律(牛顿第二定律):
即:
v0
2008.12.16
v
t
v
B
R
④能否求出这个过程的总位移呢?
微元法
Δt
取一元过程,Δt极小,vi与这一时间间隔内的平均速度相等,a的大小与元过程有关
v0
2008.12.16
v
t
v
B
R
④能否求出这个过程的总位移呢?
微元法
Δt
在使用微元法处理问题时,需将其分解为众多微小的“元过程”,而且每个“元过程”所遵循的规律是相同的,这样,我们只需分析这些“元过程”,然后再将“元过程”进行必要的数学方法(累计求和)进而使问题求解。
v0
2008.12.16
v
t
v
B
R
④能否求出这个过程的总位移呢?
⑤能否求出全过程中通过导体某个横截面的电量?
v0
2008.12.16
v
t
v
B
R
④能否求出这个过程的总位移呢?
⑤能否求出全过程中通过导体某个横截面的电量?
微元法
Δt
I
2008.12.16
F
B
R
引申1: 如图,水平放置的导体电阻为R ,R与两根光滑的平行金属导轨相连,导轨间距为L ,其间有垂直导轨平面的、磁感应强度为B的匀强磁场。导轨上有一导体棒ab质量为m受到大小为F的恒力作用从静止开始向右运动。
①导体棒将做什么运动?
加速度越来越小的加速运动,
②请描绘出运动的v-t 图像
最终做匀速运动,外力F与安培力平衡
v
t
2008.12.16
F
B
R
v
t
③末速度多大?
vm
t0
④若在t时刻,棒作匀速运动,求这段时间内的总位移。(t > t0)
t
Δt
运动规律
思考:求该过程中产生的焦耳热
2008.12.16
引申2:如图,竖直放置的光滑U形导轨宽为L,上端串有一个电容,电容为C,磁感应强度为B的匀强磁场方向垂直于纸面向里。金属棒ab的质量为m,与导轨接触良好,不计摩擦及各部分电阻,试通过计算说明金属棒的运动情况。
a
b
C
要说明运动情况,可能有哪些?
匀速,匀加速还是变加速?
找出F-t,或 a-t 的关系
需要通过计算说明什么问题?
2008.12.16
a
b
C
mg
BIL
运动规律
这种情况下,欧姆定律适用么?
恒量
即物体作匀加速直线运动!
分析元过程来帮助理解运动细节
微元
分析受力
不适用
2008.12.16
小结——微元法在电磁感应问题中的应用
在处理问题时,从对事物的极小部分(微元)分析入手,达到解决事物整体的方法。
在使用微元法处理问题时,需将其分解为众多微小的“元过程”,而且每个“元过程”所遵循的规律是相同的,这样,我们只需分析这些“元过程”,然后再将“元过程”进行必要的数学方法(累计求和)进而使问题求解。
在电磁感应问题中,常常遇到非匀变速运动过程中求位移,电量,能量等问题,灵活运用微元的思想,可以帮助我们更深刻的理解物理过程。
2008.12.16
思考题
d
d
d
d
d
d
d
P
O
N
M
v0
如图,空间等间距分布着水平方向的条形匀强磁场, 竖直方向磁场区域足够长, 磁感应强度为B=1T ,每一条形磁场区域的宽度及相邻条形磁场区域的间距均为d=0.5m,现有一边长l=0.2m、质量m=0.1kg、电阻R=0.1Ω的正方形线框MNOP以v0=7m/s的初速从左侧磁场边缘水平进入磁场
求①线框从开始进入磁场到竖直
下落的过程中产生的焦耳热Q
2008.12.16
②线框能穿过的完整条形磁场
区域的个数n。
d
d
d
d
d
d
d
P
O
N
M
v0
B、d、m、l、R、v0
微元法
∴能完整的穿过4个条形磁场区域
谢谢!
同课章节目录
