2018-2019学年湖北省黄冈市九年级(下)开学数学试卷解析版
文档属性
| 名称 | 2018-2019学年湖北省黄冈市九年级(下)开学数学试卷解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 172.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-27 20:58:26 | ||
图片预览




文档简介
2018-2019学年湖北省黄冈市九年级(下)开学数学试卷
一、选择题(下列各题的备选答案中,有且仅有一个答案是正确的,每小题3分,共24分)
1.(3分)在如图所示的花坛的图案中,圆形的内部有菊花组成的内接等边三角形,则这个图案( )
A.是轴对称图形但不是中心对称图形
B.既是轴对称图形又是中心对称图形
C.是中心对称图形但不是轴对称图形
D.既不是轴对称图形又不是中心对称图形
2.(3分)下列事件中发生的可能性为0的是( )
A.抛一枚均匀硬币,落地后正面朝上
B.今天黄冈市最高气温为 88℃
C.路边抛掷一石头,石头终将落地(空中无任何遮拦)
D.不透明袋子中放了大小相同的兵兵球和金属球,从中去摸取出兵兵球
3.(3分)对于抛物线y=(x﹣1)2+2的说法错误的是( )
A.抛物线的开口向上
B.抛物线的顶点坐标是(1,2)
C.抛物线与x轴无交点
D.当x<1时,y随x的增大而增大
4.(3分)OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )
A.80° B.40° C.50° D.20°
5.(3分)某厂一月份生产产品50台,计划二、三月份共生产产品120台,设二、三月份平均每月增长率为x,根据题意,可列出方程为( )
A.50(1+x)2=60
B.50(1+x)2=120
C.50+50(1+x)+50(1+x)2=120
D.50(1+x)+50(1+x)2=120
6.(3分)已知抛物线y=(m﹣1)x2+4x﹣3(m为常数)与x轴有两个交点,则m的取值范围是( )
A.m B.m<
C.m D.m,且m≠1
7.(3分)一个扇形的弧长是10πcm,面积是60πcm2,则此扇形的圆心角的度数是( )
A.300° B.150° C.120° D.75°
8.(3分)如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),直线x=﹣0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,某同学根据图象写出下列结论:
①a﹣b=0;
②当﹣2<x<1时,y>0;
③四边形ACBD是菱形;
④9a﹣3b+c>0
你认为其中正确的是( )
A.②③④ B.①②④ C.①③④ D.①②③
二、填空题(共8小题,每小题3分,共24分)
9.(3分)点(﹣4,3)关于原点对称的点的坐标是 .
10.(3分)把方程x2+2x﹣5=0配方后的方程为 .
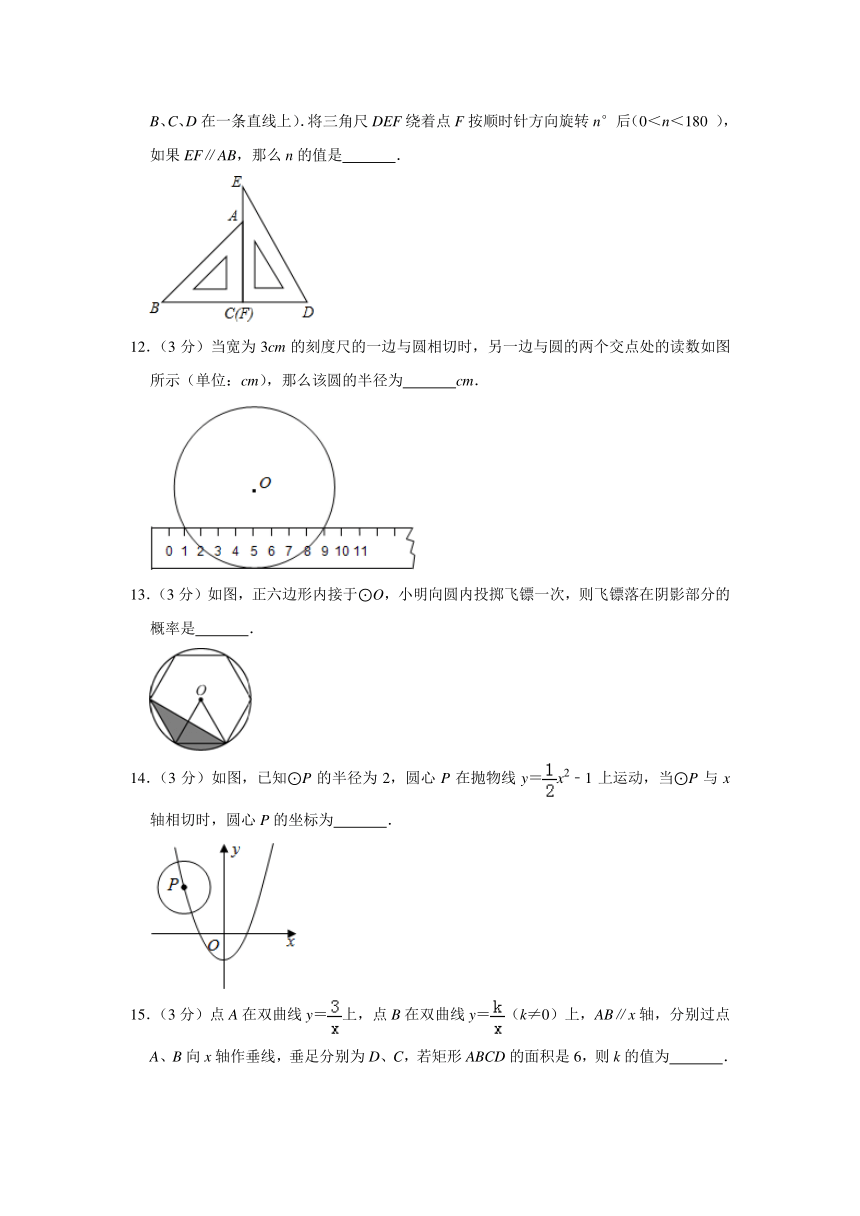
11.(3分)一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是 .
12.(3分)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为 cm.
13.(3分)如图,正六边形内接于⊙O,小明向圆内投掷飞镖一次,则飞镖落在阴影部分的概率是 .
14.(3分)如图,已知⊙P的半径为2,圆心P在抛物线y=x2﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为 .
15.(3分)点A在双曲线y=上,点B在双曲线y=(k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是6,则k的值为 .
16.(3分)如图,已知A(2,2)、B(2,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2,2)的位置,则图中阴影部分的面积为 .
三、解答题(共9小题,共72分)
17.(8分)用适当的方法解下列方程
(1)x2﹣4x﹣5=0;
(2)3x2+4x﹣1=0.
18.(6分)如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
19.(6分)某超市销售一种饮料,平均每天可售出100箱,每箱利润为120元,为了扩大销量,尽快减少库存,超市准备适当降价,据测算,若每箱降价2元,则每天可多售出4箱.
(1)如果要使每天销售该饮料获利14000元,则每箱应降价多少元.
(2)每天销售该饮料获利能达到14500元吗?若能,则每箱应降价多少?若不能,请说明理由.
20.(6分)在一个不透明的布袋里装有4个标号为1、2、3、4的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).
(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点P(x,y)在函数y=﹣x+5图象上的概率.
21.(6分)已知关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)若x1,x2满足3x1=|x2|+2,求m的值.
22.(8分)如图,一次函数y=k1x+b与反比例函数y=的图象交于A(2,3),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C.
(1)求一次函数与反比例函数的解析式;
(2)请求出△ABC的面积;
(3)若P(p,y1),Q(﹣2,y2)是函数y=图象上的两点,且y1≥y2,求实数p的取值范围.
23.(8分)如图,AB为⊙O的直径,C为中点,CD⊥BE于D.
(1)判断DC与⊙O的位置关系,并说明理由;
(2)若DC=3,⊙O半径为5,求DE长.
24.(10分)某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和利润如表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
(1)请求出y关于x的函数关系式;
(2)如果该厂每天至少投入成本26 400元,那么每天至少获利多少元?
(3)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对A产品进行让利,每瓶利润降低元,厂家如何生产可使每天获利最大?最大利润是多少?
A
B
成本(元/瓶)
50
35
利润(元/瓶)
20
15
25.(14分)如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
2018-2019学年湖北省黄冈市九年级(下)开学数学试卷
参考答案与试题解析
一、选择题(下列各题的备选答案中,有且仅有一个答案是正确的,每小题3分,共24分)
1.【解答】解:所给图形是轴对称图形,但不是中心对称图形.
故选:A.
2.【解答】解:A、抛一枚均匀硬币,落地后正面朝上,是随机事件;
B、今天黄冈市最高气温为88℃是不可能事件,可能性为0;
C、路边抛掷一石头,石头终将落地(空中无任何遮拦)是必然事件,可能性为1;
D、不透明袋子中放了大小相同的乒乓球和金属球,从中去摸取出乒乓球是随机事件;
故选:B.
3.【解答】解:∵a=1>0,∴抛物线开口向上,
∵二次函数为y=a(x﹣h)2+k顶点坐标是(h,k),
∴二次函数y=(x﹣1)2+2的图象的顶点坐标是(1,2),
∵抛物线顶点(1,2),开口向上,
∴抛物线与x轴没有交点,
故A、B、C正确
故选:D.
4.【解答】解:∵∠C=40°,
∴∠AOB=2∠C=80°.
故选:A.
5.【解答】解:设二、三月份每月的平均增长率为x,
则二月份生产机器为:50(1+x),
三月份生产机器为:50(1+x)2;
又知二、三月份共生产120台;
所以,可列方程:50(1+x)+50(1+x)2=120.
故选:D.
6.【解答】解:∵y=(m﹣1)x2+4x﹣3(m为常数)与x轴有两个交点,
∴△=16﹣4(m﹣1)(﹣3)>0,且m﹣1≠0
解得m,且m≠1.
故选:D.
7.【解答】解:∵一个扇形的弧长是10πcm,面积是60πcm2,
∴S=Rl,即60π=×R×10π,
解得:R=12,
∴S=60π=,
解得:n=150°,
故选:B.
8.【解答】解:①∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),
∴该抛物线的对称轴为x=﹣=﹣0.5,
∴a=b,a﹣b=0,①正确;
②∵抛物线开口向下,且抛物线与x轴交于点A(﹣2,0)、B(1,0),
∴当﹣2<x<1时,y>0,②正确;
③∵点A、B关于x=0.5对称,
∴AM=BM,
又∵MC=MD,且CD⊥AB,
∴四边形ACBD是菱形,③正确;
④当x=﹣3时,y<0,
即y=9a﹣3b+c<0,④错误.
综上可知:正确的结论为①②③.
故选:D.
二、填空题(共8小题,每小题3分,共24分)
9.【解答】解:根据关于原点对称的点的坐标的特点,
∴点(﹣4,3)关于原点对称的点的坐标是(4,﹣3).
故答案为(4,﹣3).
10.【解答】解:x2+2x﹣5=0,
x2+2x=5,
x2+2x+1=5+1,
(x+1)2=6,
故答案为:(x+1)2=6.
11.【解答】解:①如图1中,EF∥AB时,∠ACE=∠A=45°,
∴旋转角n=45时,EF∥AB.
②如图2中,EF∥AB时,∠ACE+∠A=180°,
∴∠ACE=135°
∴旋转角n=360﹣135=225,
∵0<n<180,
∴此种情形不合题意,
故答案为45
12.【解答】解:连接OA,过点O作OD⊥AB于点D,
∵OD⊥AB,
∴AD=AB=(9﹣1)=4cm,
设OA=r,则OD=r﹣3,
在Rt△OAD中,
OA2﹣OD2=AD2,即r2﹣(r﹣3)2=42,解得r=cm.
故答案为:.
13.【解答】解:如图所示:连接OA,
∵正六边形内接于⊙O,
∴△OAB,△OBC都是等边三角形,
∴∠AOB=∠OBC=60°,
∴OC∥AB,
∴S△ABC=S△OBC,
∴S阴=S扇形OBC,
则飞镖落在阴影部分的概率是;
故答案为:.
14.【解答】解:依题意,可设P(x,2)或P(x,﹣2).
①当P的坐标是(x,2)时,将其代入y=x2﹣1,得
2=x2﹣1,
解得x=±,
此时P(,2)或(﹣,2);
②当P的坐标是(x,﹣2)时,将其代入y=x2﹣1,得
﹣2=x2﹣1,即﹣1=x2
无解.
综上所述,符合条件的点P的坐标是(,2)或(﹣,2);
故答案是:(,2)或(﹣,2).
15.【解答】解:设A(a,),则B(,)
∴AB=
∵SABCD=AB×AD
∴()×=6
∴k=9
故答案为9
16.【解答】解:∵A(2,2)、B(2,1),
∴OA=4,OB=,
∵由A(2,2)使点A旋转到点A′(﹣2,2),
∴∠A′OA=∠B′OB=90°,
根据旋转的性质可得,S=SOBC,
∴阴影部分的面积等于S扇形A'OA﹣S扇形C'OC=π×42﹣π×()2=,
故答案为:π.
三、解答题(共9小题,共72分)
17.【解答】解:(1)(x﹣5)(x+1)=0,
x﹣5=0或x+1=0,
∴x1=5,x2=﹣1;
(2)∵a=3,b=4,c=﹣1,
∴b2﹣4ac=28>0,
∴x==,
∴x1=,x2=.
18.【解答】(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°,
∵AB⊥BC,
∴∠ABC=90°,
∴∠DBE=∠CBE=30°,
在△BDE和△BCE中,
∵,
∴△BDE≌△BCE(SAS);
(2)四边形ABED为菱形;
由(1)得△BDE≌△BCE,
∵△BAD是由△BEC旋转而得,
∴△BAD≌△BEC,
∴BA=BE,AD=EC=ED,
又∵BE=CE,
∴四边形ABED为菱形.
19.【解答】解:(1)要使每天销售饮料获利14000元,每箱应降价x元,
依据题意列方程得,(120﹣x)(100+2x)=14000,
整理得x2﹣70x+1000=0,
解得x1=20,x2=50;
∵为了扩大销量,尽快减少库存,
∴x=50.
答:每箱应降价50元,可使每天销售饮料获利14000元.
(2)由题意得:(120﹣x)(100+2x)=14500,
整理得x2﹣70x+1250=0,
∵△=702﹣4×1250<0,
∴此方程无实数根,
故该超市每天销售这种饮料的获利不可能达14500元.
20.【解答】解:列表得:
y
x
(x,y)
1
2
3
4
1
(1,2)
(1,3)
(1,4)
2
(2,1)
(2,3)
(2,4)
3
(3,1)
(3,2)
(3,4)
4
(4,1)
(4,2)
(4,3)
(1)点P所有可能的坐标有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12种;
(2)∵共有12种等可能的结果,其中在函数y=﹣x+5图象上的有4种,
即:(1,4),(2,3),(3,2),(4,1)
∴点P(x,y)在函数y=﹣x+5图象上的概率为:P=.
21.【解答】解:(1)∵关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2,
∴△=(﹣6)2﹣4(m+4)=20﹣4m≥0,
解得:m≤5,
∴m的取值范围为m≤5.
(2)∵关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2,
∴x1+x2=6①,x1?x2=m+4②.
∵3x1=|x2|+2,
当x2≥0时,有3x1=x2+2③,
联立①③解得:x1=2,x2=4,
∴8=m+4,m=4;
当x2<0时,有3x1=﹣x2+2④,
联立①④解得:x1=﹣2,x2=8(不合题意,舍去).
∴符合条件的m的值为4.
22.【解答】解:(1)把A(2,3)代入y=,得k2=6,
∴反比例函数的解析式是y=;
∵B(n,﹣2)在反比例函数y=的图象上,
∴n=﹣3,
即B的坐标为(﹣3,﹣2),
把A(2,3),B(﹣3,﹣2)代入y=k1x+b,得
,解得,,
即一次函数的解析式为y=x+1;
(2)∵BC⊥x轴,B(﹣3,﹣2),A(2,3)
∴BC=2,
∴S△ABC=?BC?|2﹣(﹣3)|==5;
(3)∵P(p,y1),Q(﹣2,y2)是函数y=图象上的两点,且y1≥y2,
∴当点P在第三象限时,要使y1≥y2,实数p的取值范围是p≤﹣2,
当点P在第一象限时,要使y1≥y2,实数p的取值范围是p>0,
即p的取值范围是p≤﹣2或p>0.
23.【解答】解:(1)DC与⊙O相切.理由如下:
连结AE、OC,它们相交于F点,如图,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵CD⊥BE,
∴∠D=90°,
∴CD∥AE,
又∵C为中点,
∴OC⊥AE,AF=EF,
∴OC⊥CD,
∴CD为⊙O的切线;
(2)∵∠D=∠DCF=∠CFE=90°,
∴四边形CFED为矩形,
∴EF=CD=3,DE=CF,
∴AF=3,
在Rt△OFA中,OA=5,
∴OF==4,
∴CF=OC﹣OF=5﹣4=1,
∴DE=1.
24.【解答】解:(1)根据题意可得:
y=20x+15(600﹣x)
=5x+9000.
∴y关于x的函数关系式为y=5x+9000;
(2)根据题意,得:
50 x+35(600﹣x)≥26400,
解得:x≥360,
∵y=5x+9000,5>0,
∴y随x的增大而增大,
∴当x=360时,y有最小值为10800,
∴每天至少获利10800元;
(3)根据题意可得:
y=(20﹣)x+15(600﹣x)
=﹣(x﹣250)2+9625,
∵,∴当x=250时,y有最大值9625,
∴每天生产A产品250件,B产品350件获利最大,最大利润为9625元.
25.【解答】解:(1)由抛物线y=﹣x2+bx+c过点A(﹣1,0)及C(2,3)得,
,
解得,
故抛物线为y=﹣x2+2x+3;
又设直线为y=kx+n过点A(﹣1,0)及C(2,3),
得,
解得,
故直线AC为y=x+1;
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4),
当x=1时,y=x+1=2,
∴B(1,2),
∵点E在直线AC上,设E(x,x+1).
①如图2,当点E在线段AC上时,点F在点E上方,则F(x,x+3),
∵F在抛物线上,
∴x+3=﹣x2+2x+3,
解得,x=0或x=1(舍去),
∴E(0,1);
②当点E在线段AC(或CA)延长线上时,点F在点E下方,则F(x,x﹣1),
∵F在抛物线上,
∴x﹣1=﹣x2+2x+3,
解得x=或x=,
∴E(,)或(,),
综上,满足条件的点E的坐标为(0,1)或(,)或(,);
(3)方法一:如图3,过点P作PQ⊥x轴交AC于点Q,交x轴于点H;过点C作CG⊥x轴于点G,设Q(x,x+1),则P(x,﹣x2+2x+3)
∴PQ=(﹣x2+2x+3)﹣(x+1)
=﹣x2+x+2
又∵S△APC=S△APQ+S△CPQ
=PQ?AG
=(﹣x2+x+2)×3
=﹣(x﹣)2+,
∴面积的最大值为;
方法二:过点P作PQ⊥x轴交AC于点Q,交x轴于点H;过点C作CG⊥x轴于点G,如图3,
设Q(x,x+1),则P(x,﹣x2+2x+3)
又∵S△APC=S△APH+S直角梯形PHGC﹣S△AGC
=(x+1)(﹣x2+2x+3)+(﹣x2+2x+3+3)(2﹣x)﹣×3×3
=﹣x2+x+3
=﹣(x﹣)2+,
∴△APC的面积的最大值为.
一、选择题(下列各题的备选答案中,有且仅有一个答案是正确的,每小题3分,共24分)
1.(3分)在如图所示的花坛的图案中,圆形的内部有菊花组成的内接等边三角形,则这个图案( )
A.是轴对称图形但不是中心对称图形
B.既是轴对称图形又是中心对称图形
C.是中心对称图形但不是轴对称图形
D.既不是轴对称图形又不是中心对称图形
2.(3分)下列事件中发生的可能性为0的是( )
A.抛一枚均匀硬币,落地后正面朝上
B.今天黄冈市最高气温为 88℃
C.路边抛掷一石头,石头终将落地(空中无任何遮拦)
D.不透明袋子中放了大小相同的兵兵球和金属球,从中去摸取出兵兵球
3.(3分)对于抛物线y=(x﹣1)2+2的说法错误的是( )
A.抛物线的开口向上
B.抛物线的顶点坐标是(1,2)
C.抛物线与x轴无交点
D.当x<1时,y随x的增大而增大
4.(3分)OA,OB是⊙O的两条半径,且∠C=40°,点C在⊙O上,则∠AOB的度数为( )
A.80° B.40° C.50° D.20°
5.(3分)某厂一月份生产产品50台,计划二、三月份共生产产品120台,设二、三月份平均每月增长率为x,根据题意,可列出方程为( )
A.50(1+x)2=60
B.50(1+x)2=120
C.50+50(1+x)+50(1+x)2=120
D.50(1+x)+50(1+x)2=120
6.(3分)已知抛物线y=(m﹣1)x2+4x﹣3(m为常数)与x轴有两个交点,则m的取值范围是( )
A.m B.m<
C.m D.m,且m≠1
7.(3分)一个扇形的弧长是10πcm,面积是60πcm2,则此扇形的圆心角的度数是( )
A.300° B.150° C.120° D.75°
8.(3分)如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),直线x=﹣0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,某同学根据图象写出下列结论:
①a﹣b=0;
②当﹣2<x<1时,y>0;
③四边形ACBD是菱形;
④9a﹣3b+c>0
你认为其中正确的是( )
A.②③④ B.①②④ C.①③④ D.①②③
二、填空题(共8小题,每小题3分,共24分)
9.(3分)点(﹣4,3)关于原点对称的点的坐标是 .
10.(3分)把方程x2+2x﹣5=0配方后的方程为 .
11.(3分)一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是 .
12.(3分)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为 cm.
13.(3分)如图,正六边形内接于⊙O,小明向圆内投掷飞镖一次,则飞镖落在阴影部分的概率是 .
14.(3分)如图,已知⊙P的半径为2,圆心P在抛物线y=x2﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为 .
15.(3分)点A在双曲线y=上,点B在双曲线y=(k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是6,则k的值为 .
16.(3分)如图,已知A(2,2)、B(2,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2,2)的位置,则图中阴影部分的面积为 .
三、解答题(共9小题,共72分)
17.(8分)用适当的方法解下列方程
(1)x2﹣4x﹣5=0;
(2)3x2+4x﹣1=0.
18.(6分)如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
19.(6分)某超市销售一种饮料,平均每天可售出100箱,每箱利润为120元,为了扩大销量,尽快减少库存,超市准备适当降价,据测算,若每箱降价2元,则每天可多售出4箱.
(1)如果要使每天销售该饮料获利14000元,则每箱应降价多少元.
(2)每天销售该饮料获利能达到14500元吗?若能,则每箱应降价多少?若不能,请说明理由.
20.(6分)在一个不透明的布袋里装有4个标号为1、2、3、4的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).
(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点P(x,y)在函数y=﹣x+5图象上的概率.
21.(6分)已知关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)若x1,x2满足3x1=|x2|+2,求m的值.
22.(8分)如图,一次函数y=k1x+b与反比例函数y=的图象交于A(2,3),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C.
(1)求一次函数与反比例函数的解析式;
(2)请求出△ABC的面积;
(3)若P(p,y1),Q(﹣2,y2)是函数y=图象上的两点,且y1≥y2,求实数p的取值范围.
23.(8分)如图,AB为⊙O的直径,C为中点,CD⊥BE于D.
(1)判断DC与⊙O的位置关系,并说明理由;
(2)若DC=3,⊙O半径为5,求DE长.
24.(10分)某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和利润如表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
(1)请求出y关于x的函数关系式;
(2)如果该厂每天至少投入成本26 400元,那么每天至少获利多少元?
(3)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对A产品进行让利,每瓶利润降低元,厂家如何生产可使每天获利最大?最大利润是多少?
A
B
成本(元/瓶)
50
35
利润(元/瓶)
20
15
25.(14分)如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
2018-2019学年湖北省黄冈市九年级(下)开学数学试卷
参考答案与试题解析
一、选择题(下列各题的备选答案中,有且仅有一个答案是正确的,每小题3分,共24分)
1.【解答】解:所给图形是轴对称图形,但不是中心对称图形.
故选:A.
2.【解答】解:A、抛一枚均匀硬币,落地后正面朝上,是随机事件;
B、今天黄冈市最高气温为88℃是不可能事件,可能性为0;
C、路边抛掷一石头,石头终将落地(空中无任何遮拦)是必然事件,可能性为1;
D、不透明袋子中放了大小相同的乒乓球和金属球,从中去摸取出乒乓球是随机事件;
故选:B.
3.【解答】解:∵a=1>0,∴抛物线开口向上,
∵二次函数为y=a(x﹣h)2+k顶点坐标是(h,k),
∴二次函数y=(x﹣1)2+2的图象的顶点坐标是(1,2),
∵抛物线顶点(1,2),开口向上,
∴抛物线与x轴没有交点,
故A、B、C正确
故选:D.
4.【解答】解:∵∠C=40°,
∴∠AOB=2∠C=80°.
故选:A.
5.【解答】解:设二、三月份每月的平均增长率为x,
则二月份生产机器为:50(1+x),
三月份生产机器为:50(1+x)2;
又知二、三月份共生产120台;
所以,可列方程:50(1+x)+50(1+x)2=120.
故选:D.
6.【解答】解:∵y=(m﹣1)x2+4x﹣3(m为常数)与x轴有两个交点,
∴△=16﹣4(m﹣1)(﹣3)>0,且m﹣1≠0
解得m,且m≠1.
故选:D.
7.【解答】解:∵一个扇形的弧长是10πcm,面积是60πcm2,
∴S=Rl,即60π=×R×10π,
解得:R=12,
∴S=60π=,
解得:n=150°,
故选:B.
8.【解答】解:①∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),
∴该抛物线的对称轴为x=﹣=﹣0.5,
∴a=b,a﹣b=0,①正确;
②∵抛物线开口向下,且抛物线与x轴交于点A(﹣2,0)、B(1,0),
∴当﹣2<x<1时,y>0,②正确;
③∵点A、B关于x=0.5对称,
∴AM=BM,
又∵MC=MD,且CD⊥AB,
∴四边形ACBD是菱形,③正确;
④当x=﹣3时,y<0,
即y=9a﹣3b+c<0,④错误.
综上可知:正确的结论为①②③.
故选:D.
二、填空题(共8小题,每小题3分,共24分)
9.【解答】解:根据关于原点对称的点的坐标的特点,
∴点(﹣4,3)关于原点对称的点的坐标是(4,﹣3).
故答案为(4,﹣3).
10.【解答】解:x2+2x﹣5=0,
x2+2x=5,
x2+2x+1=5+1,
(x+1)2=6,
故答案为:(x+1)2=6.
11.【解答】解:①如图1中,EF∥AB时,∠ACE=∠A=45°,
∴旋转角n=45时,EF∥AB.
②如图2中,EF∥AB时,∠ACE+∠A=180°,
∴∠ACE=135°
∴旋转角n=360﹣135=225,
∵0<n<180,
∴此种情形不合题意,
故答案为45
12.【解答】解:连接OA,过点O作OD⊥AB于点D,
∵OD⊥AB,
∴AD=AB=(9﹣1)=4cm,
设OA=r,则OD=r﹣3,
在Rt△OAD中,
OA2﹣OD2=AD2,即r2﹣(r﹣3)2=42,解得r=cm.
故答案为:.
13.【解答】解:如图所示:连接OA,
∵正六边形内接于⊙O,
∴△OAB,△OBC都是等边三角形,
∴∠AOB=∠OBC=60°,
∴OC∥AB,
∴S△ABC=S△OBC,
∴S阴=S扇形OBC,
则飞镖落在阴影部分的概率是;
故答案为:.
14.【解答】解:依题意,可设P(x,2)或P(x,﹣2).
①当P的坐标是(x,2)时,将其代入y=x2﹣1,得
2=x2﹣1,
解得x=±,
此时P(,2)或(﹣,2);
②当P的坐标是(x,﹣2)时,将其代入y=x2﹣1,得
﹣2=x2﹣1,即﹣1=x2
无解.
综上所述,符合条件的点P的坐标是(,2)或(﹣,2);
故答案是:(,2)或(﹣,2).
15.【解答】解:设A(a,),则B(,)
∴AB=
∵SABCD=AB×AD
∴()×=6
∴k=9
故答案为9
16.【解答】解:∵A(2,2)、B(2,1),
∴OA=4,OB=,
∵由A(2,2)使点A旋转到点A′(﹣2,2),
∴∠A′OA=∠B′OB=90°,
根据旋转的性质可得,S=SOBC,
∴阴影部分的面积等于S扇形A'OA﹣S扇形C'OC=π×42﹣π×()2=,
故答案为:π.
三、解答题(共9小题,共72分)
17.【解答】解:(1)(x﹣5)(x+1)=0,
x﹣5=0或x+1=0,
∴x1=5,x2=﹣1;
(2)∵a=3,b=4,c=﹣1,
∴b2﹣4ac=28>0,
∴x==,
∴x1=,x2=.
18.【解答】(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°,
∵AB⊥BC,
∴∠ABC=90°,
∴∠DBE=∠CBE=30°,
在△BDE和△BCE中,
∵,
∴△BDE≌△BCE(SAS);
(2)四边形ABED为菱形;
由(1)得△BDE≌△BCE,
∵△BAD是由△BEC旋转而得,
∴△BAD≌△BEC,
∴BA=BE,AD=EC=ED,
又∵BE=CE,
∴四边形ABED为菱形.
19.【解答】解:(1)要使每天销售饮料获利14000元,每箱应降价x元,
依据题意列方程得,(120﹣x)(100+2x)=14000,
整理得x2﹣70x+1000=0,
解得x1=20,x2=50;
∵为了扩大销量,尽快减少库存,
∴x=50.
答:每箱应降价50元,可使每天销售饮料获利14000元.
(2)由题意得:(120﹣x)(100+2x)=14500,
整理得x2﹣70x+1250=0,
∵△=702﹣4×1250<0,
∴此方程无实数根,
故该超市每天销售这种饮料的获利不可能达14500元.
20.【解答】解:列表得:
y
x
(x,y)
1
2
3
4
1
(1,2)
(1,3)
(1,4)
2
(2,1)
(2,3)
(2,4)
3
(3,1)
(3,2)
(3,4)
4
(4,1)
(4,2)
(4,3)
(1)点P所有可能的坐标有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12种;
(2)∵共有12种等可能的结果,其中在函数y=﹣x+5图象上的有4种,
即:(1,4),(2,3),(3,2),(4,1)
∴点P(x,y)在函数y=﹣x+5图象上的概率为:P=.
21.【解答】解:(1)∵关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2,
∴△=(﹣6)2﹣4(m+4)=20﹣4m≥0,
解得:m≤5,
∴m的取值范围为m≤5.
(2)∵关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2,
∴x1+x2=6①,x1?x2=m+4②.
∵3x1=|x2|+2,
当x2≥0时,有3x1=x2+2③,
联立①③解得:x1=2,x2=4,
∴8=m+4,m=4;
当x2<0时,有3x1=﹣x2+2④,
联立①④解得:x1=﹣2,x2=8(不合题意,舍去).
∴符合条件的m的值为4.
22.【解答】解:(1)把A(2,3)代入y=,得k2=6,
∴反比例函数的解析式是y=;
∵B(n,﹣2)在反比例函数y=的图象上,
∴n=﹣3,
即B的坐标为(﹣3,﹣2),
把A(2,3),B(﹣3,﹣2)代入y=k1x+b,得
,解得,,
即一次函数的解析式为y=x+1;
(2)∵BC⊥x轴,B(﹣3,﹣2),A(2,3)
∴BC=2,
∴S△ABC=?BC?|2﹣(﹣3)|==5;
(3)∵P(p,y1),Q(﹣2,y2)是函数y=图象上的两点,且y1≥y2,
∴当点P在第三象限时,要使y1≥y2,实数p的取值范围是p≤﹣2,
当点P在第一象限时,要使y1≥y2,实数p的取值范围是p>0,
即p的取值范围是p≤﹣2或p>0.
23.【解答】解:(1)DC与⊙O相切.理由如下:
连结AE、OC,它们相交于F点,如图,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵CD⊥BE,
∴∠D=90°,
∴CD∥AE,
又∵C为中点,
∴OC⊥AE,AF=EF,
∴OC⊥CD,
∴CD为⊙O的切线;
(2)∵∠D=∠DCF=∠CFE=90°,
∴四边形CFED为矩形,
∴EF=CD=3,DE=CF,
∴AF=3,
在Rt△OFA中,OA=5,
∴OF==4,
∴CF=OC﹣OF=5﹣4=1,
∴DE=1.
24.【解答】解:(1)根据题意可得:
y=20x+15(600﹣x)
=5x+9000.
∴y关于x的函数关系式为y=5x+9000;
(2)根据题意,得:
50 x+35(600﹣x)≥26400,
解得:x≥360,
∵y=5x+9000,5>0,
∴y随x的增大而增大,
∴当x=360时,y有最小值为10800,
∴每天至少获利10800元;
(3)根据题意可得:
y=(20﹣)x+15(600﹣x)
=﹣(x﹣250)2+9625,
∵,∴当x=250时,y有最大值9625,
∴每天生产A产品250件,B产品350件获利最大,最大利润为9625元.
25.【解答】解:(1)由抛物线y=﹣x2+bx+c过点A(﹣1,0)及C(2,3)得,
,
解得,
故抛物线为y=﹣x2+2x+3;
又设直线为y=kx+n过点A(﹣1,0)及C(2,3),
得,
解得,
故直线AC为y=x+1;
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4),
当x=1时,y=x+1=2,
∴B(1,2),
∵点E在直线AC上,设E(x,x+1).
①如图2,当点E在线段AC上时,点F在点E上方,则F(x,x+3),
∵F在抛物线上,
∴x+3=﹣x2+2x+3,
解得,x=0或x=1(舍去),
∴E(0,1);
②当点E在线段AC(或CA)延长线上时,点F在点E下方,则F(x,x﹣1),
∵F在抛物线上,
∴x﹣1=﹣x2+2x+3,
解得x=或x=,
∴E(,)或(,),
综上,满足条件的点E的坐标为(0,1)或(,)或(,);
(3)方法一:如图3,过点P作PQ⊥x轴交AC于点Q,交x轴于点H;过点C作CG⊥x轴于点G,设Q(x,x+1),则P(x,﹣x2+2x+3)
∴PQ=(﹣x2+2x+3)﹣(x+1)
=﹣x2+x+2
又∵S△APC=S△APQ+S△CPQ
=PQ?AG
=(﹣x2+x+2)×3
=﹣(x﹣)2+,
∴面积的最大值为;
方法二:过点P作PQ⊥x轴交AC于点Q,交x轴于点H;过点C作CG⊥x轴于点G,如图3,
设Q(x,x+1),则P(x,﹣x2+2x+3)
又∵S△APC=S△APH+S直角梯形PHGC﹣S△AGC
=(x+1)(﹣x2+2x+3)+(﹣x2+2x+3+3)(2﹣x)﹣×3×3
=﹣x2+x+3
=﹣(x﹣)2+,
∴△APC的面积的最大值为.
同课章节目录
