6.2.1方程的简单变形(一)教案
图片预览

文档简介
6.2解一元一次方程
6.2.1方程的简单变形(一)
【学习目标】
通过天平实验,让学生在观察、思考的基础上归纳出方程的两种变形,并能利用它们将简单的方程变形以求出未知数的值.
【学习重点】
方程的两种变形
【学习难点】
由具体实例抽象出方程的两种变形
【探究学习】
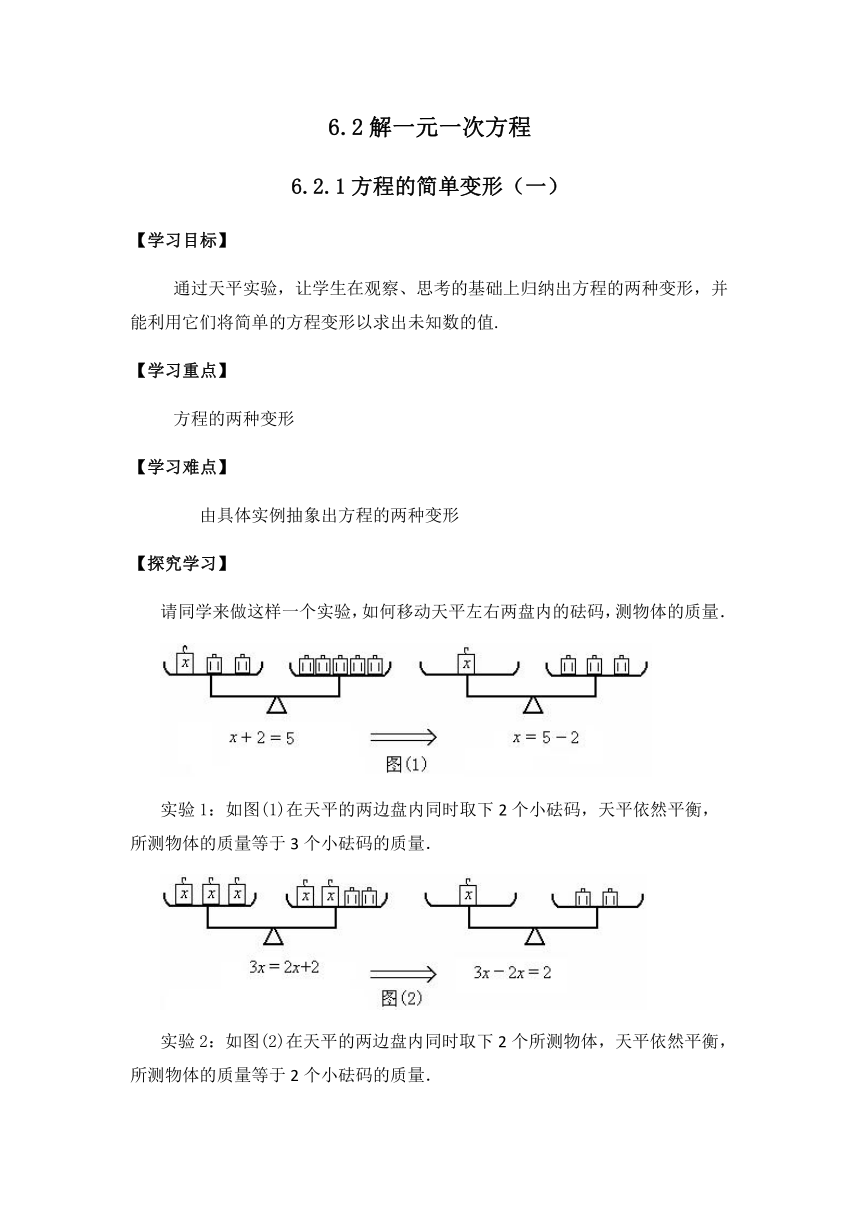
请同学来做这样一个实验,如何移动天平左右两盘内的砝码,测物体的质量.
实验1:如图(1)在天平的两边盘内同时取下2个小砝码,天平依然平衡,所测物体的质量等于3个小砝码的质量.
实验2:如图(2)在天平的两边盘内同时取下2个所测物体,天平依然平衡,所测物体的质量等于2个小砝码的质量.
实验3:如图(3)将天平两边盘内物体的质量同时缩少到原来的二分之一,天平依然平衡,所测物体的质量等于3个小砝码的质量.
上面的实验操作过程,反映了方程的变形过程,从这个变形过程,你发现了什么一般规律?
方程是这样变形的:
方程的两边都加上或都减去同一个数或同一个整式,方程的解不变.
方程两边都乘以或都除以同一个不为零的数,方程的解不变.
请同学们回忆等式的性质和方程的变形规律有何相同之处?并请思考为什么它们有相同之处?
通过实验操作,可求得物体的质量,同样通过对方程进行适当的变形,可以求得方程的解.
【典型例题】
例1: 解下列方程.
(1)x-5 = 7; (2)4x = 3x-4.
分析:(1)利用方程的变形规律,在方程x-5 = 7的两边同时加上5,即x -5 + 5 = 7 + 5,可求得方程的解.
(2)利用方程的变形规律,在方程4x = 3x-4的两边同时减去3x,即4x-3xx = 3xx-3x-4,可求得方程的解.
即 x= 12.
即 x =-4 .
像上面,将方程中的某些项改变符号后,从方程的一边移到另一边的变形叫做移项(transposition).
注 (1)上面两小题方程变形中,均把含未知数x的项,移到方程的左边,而把常数项移到了方程的右边.
(2)移项需变号,即:跃过等号,改变符号.
例2: 解下列方程:
(1)-5x= 2; (2) ;
分析:(1)利用方程的变形规律,在方程-5x= 2的两边同除以-5,即-5x÷(-5)= 2÷(-5)(或),也就是x=,可求得方程的解.
(2)利用方程的变形规律,在方程的两边同除以或同乘以,即(或),可求得方程的解.
解:?(1)方程两边都除以-5,得
x= .
(2)方程两边都除以,得
x= ,
即x = .
或解 方程两边同乘以,得
x = .
注:1.上面两题的变形通常称作“将未知数的系数化为1” .
2.上面两个解方程的过程,都是对方程进行适当的变形,得到x = a的形式.
例3:下面是方程x + 3 = 8的三种解法,请指出对与错,并说明为什么?
(1)x + 3 = 8 = x = 8-3 = 5;
(2)x+ 3 = 8,移项得x = 8 + 3,所以x = 11;
(3)x + 3 = 8移项得x = 8-3 , 所以x= 5.
解: (1)这种解法是错的.变形后新方程两边的值和原方程两边的值不相等,所以解方程时不能连等;
(2)这种解法也是错误的,移项要变号;
(3)这种解法是正确的.
【学习小结】
1.把方程两边都加上或减去同一个数或整式方程的解不变.
2.把方程两边都乘以或除以(不等零)的同一个数,方程的解不变.第①种变形又叫移项,移项别忘了要先变号,注意移项与在方程的一边交换两项的位置有本质的区别.
【反馈检测】
1.判断下列方程的解法对不对?如果不对,应怎样改正.
(1)9x = -4,得x= ;
(2),得x= 1;
(3),得x = 2;
(4),得y =;
(5)3 + x = 5,得x = 5 + 3;
(6)3 =x-2,得x = -2-3 .
2.(口答)求下列方程的解.
(1)x-6 = 6; (2)7x= 6x-4;
(3)-5x= 60; (4).
3.下面的移项对不对?如果不对,错在哪里?应当怎样改正?
(1)从7 +x= 13,得到x = 13 + 7;
(2)从5x = 4x + 8,得到5x - 4x = 8
4.用方程的变形解方程:44x+ 64 = 328.
6.2.1方程的简单变形(一)
【学习目标】
通过天平实验,让学生在观察、思考的基础上归纳出方程的两种变形,并能利用它们将简单的方程变形以求出未知数的值.
【学习重点】
方程的两种变形
【学习难点】
由具体实例抽象出方程的两种变形
【探究学习】
请同学来做这样一个实验,如何移动天平左右两盘内的砝码,测物体的质量.
实验1:如图(1)在天平的两边盘内同时取下2个小砝码,天平依然平衡,所测物体的质量等于3个小砝码的质量.
实验2:如图(2)在天平的两边盘内同时取下2个所测物体,天平依然平衡,所测物体的质量等于2个小砝码的质量.
实验3:如图(3)将天平两边盘内物体的质量同时缩少到原来的二分之一,天平依然平衡,所测物体的质量等于3个小砝码的质量.
上面的实验操作过程,反映了方程的变形过程,从这个变形过程,你发现了什么一般规律?
方程是这样变形的:
方程的两边都加上或都减去同一个数或同一个整式,方程的解不变.
方程两边都乘以或都除以同一个不为零的数,方程的解不变.
请同学们回忆等式的性质和方程的变形规律有何相同之处?并请思考为什么它们有相同之处?
通过实验操作,可求得物体的质量,同样通过对方程进行适当的变形,可以求得方程的解.
【典型例题】
例1: 解下列方程.
(1)x-5 = 7; (2)4x = 3x-4.
分析:(1)利用方程的变形规律,在方程x-5 = 7的两边同时加上5,即x -5 + 5 = 7 + 5,可求得方程的解.
(2)利用方程的变形规律,在方程4x = 3x-4的两边同时减去3x,即4x-3xx = 3xx-3x-4,可求得方程的解.
即 x= 12.
即 x =-4 .
像上面,将方程中的某些项改变符号后,从方程的一边移到另一边的变形叫做移项(transposition).
注 (1)上面两小题方程变形中,均把含未知数x的项,移到方程的左边,而把常数项移到了方程的右边.
(2)移项需变号,即:跃过等号,改变符号.
例2: 解下列方程:
(1)-5x= 2; (2) ;
分析:(1)利用方程的变形规律,在方程-5x= 2的两边同除以-5,即-5x÷(-5)= 2÷(-5)(或),也就是x=,可求得方程的解.
(2)利用方程的变形规律,在方程的两边同除以或同乘以,即(或),可求得方程的解.
解:?(1)方程两边都除以-5,得
x= .
(2)方程两边都除以,得
x= ,
即x = .
或解 方程两边同乘以,得
x = .
注:1.上面两题的变形通常称作“将未知数的系数化为1” .
2.上面两个解方程的过程,都是对方程进行适当的变形,得到x = a的形式.
例3:下面是方程x + 3 = 8的三种解法,请指出对与错,并说明为什么?
(1)x + 3 = 8 = x = 8-3 = 5;
(2)x+ 3 = 8,移项得x = 8 + 3,所以x = 11;
(3)x + 3 = 8移项得x = 8-3 , 所以x= 5.
解: (1)这种解法是错的.变形后新方程两边的值和原方程两边的值不相等,所以解方程时不能连等;
(2)这种解法也是错误的,移项要变号;
(3)这种解法是正确的.
【学习小结】
1.把方程两边都加上或减去同一个数或整式方程的解不变.
2.把方程两边都乘以或除以(不等零)的同一个数,方程的解不变.第①种变形又叫移项,移项别忘了要先变号,注意移项与在方程的一边交换两项的位置有本质的区别.
【反馈检测】
1.判断下列方程的解法对不对?如果不对,应怎样改正.
(1)9x = -4,得x= ;
(2),得x= 1;
(3),得x = 2;
(4),得y =;
(5)3 + x = 5,得x = 5 + 3;
(6)3 =x-2,得x = -2-3 .
2.(口答)求下列方程的解.
(1)x-6 = 6; (2)7x= 6x-4;
(3)-5x= 60; (4).
3.下面的移项对不对?如果不对,错在哪里?应当怎样改正?
(1)从7 +x= 13,得到x = 13 + 7;
(2)从5x = 4x + 8,得到5x - 4x = 8
4.用方程的变形解方程:44x+ 64 = 328.
