九年级数学上册第六章反比例函数复习教案
文档属性
| 名称 | 九年级数学上册第六章反比例函数复习教案 |  | |
| 格式 | zip | ||
| 文件大小 | 374.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-28 15:31:19 | ||
图片预览

文档简介
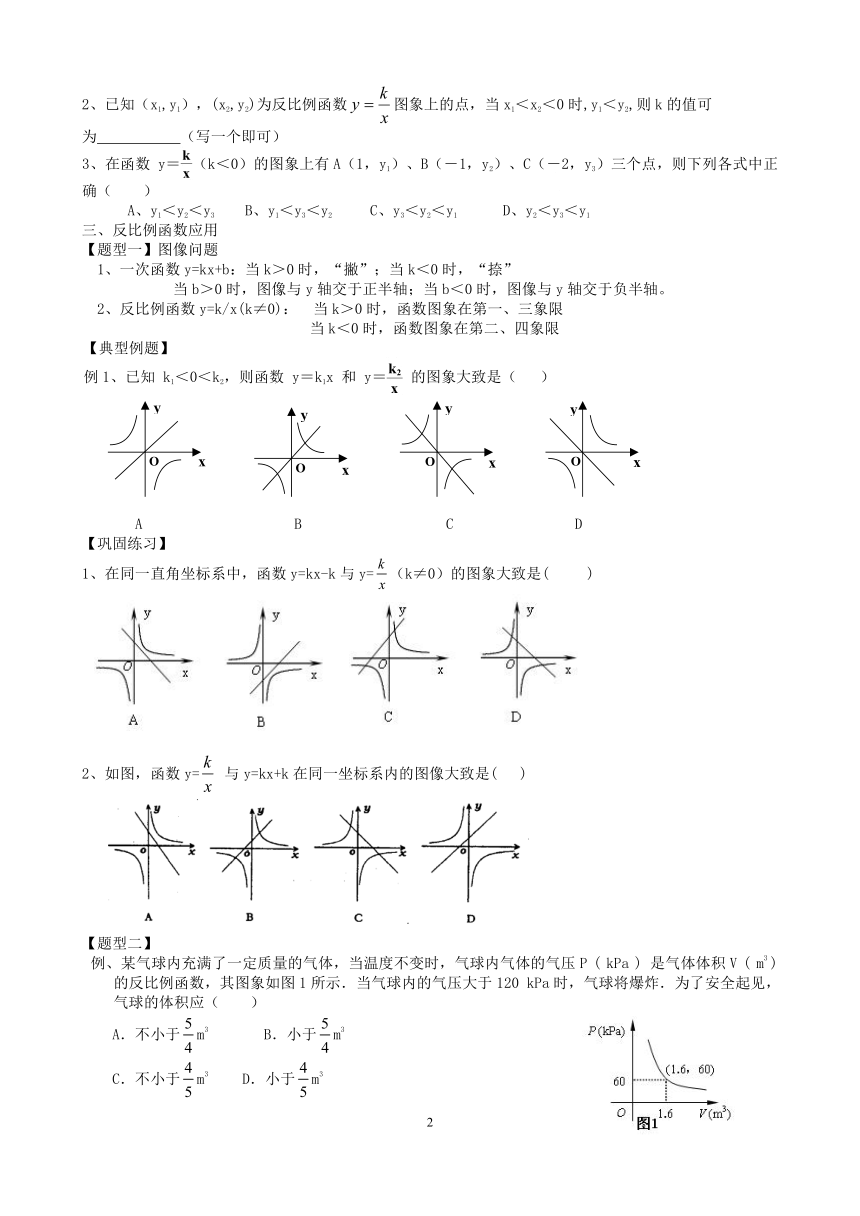
九年级数学上册第六章《反比例函数》 复习
一、反比例函数定义
【知识要点】
一般地,如果两个变量x、y之间的关系可以表示成y= (k为常数,k≠0)的形式,那么称y是x的反比例函数.
【巩固练习】
1、已知反比例函数的图象经过点,则这个反比例函数的解析式是 .
2、近视眼镜的度数(度)与镜片焦距(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数与镜片焦距之间的函数关系式为 .
二、 反比例函数的图象和性质
【知识要点】
【题型一】象限与点
1、反比例函数(m-1)的图象在第二、四象限,则m=
2、点(5,-6)在反比例函数的图像上,那么k=_________,该反比例函数的图像位于第_______象限.
3、如果双曲线y=经过点(-2,3),那么此双曲线也经过点
(A)(-2,-3) (B)(3,2) (C)(3,-2) (D)(-3,-2)
4、如果反比例函数的图像经过点(-3,),那么直线y=kx-k一定经过点(—2,___).
【题型二】增减性问题
当k>0时,函数图象在第一、三象限,y随x的增大而减小
当k<0时,函数图象在第二、四象限,y随x的增大而增大
【典型例题】
例1:已知点A()、B()是反比例函数()图象上的两点,若,则有( )
A. B. C. D.
【巩固练习】
1、在反比例函数图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是 ( )
A.k>3 B.k>0 C.k<3 D. k<0
2、已知(x1,y1),(x2,y2)为反比例函数图象上的点,当x1<x2<0时,y1<y2,则k的值可
为 (写一个即可)
3、在函数 y=(k<0)的图象上有A(1,y1)、B(-1,y2)、C(-2,y3)三个点,则下列各式中正确( )
A、y1<y2<y3 B、y1<y3<y2 C、y3<y2<y1 D、y2<y3<y1
三、反比例函数应用
【题型一】图像问题
1、一次函数y=kx+b:当k>0时,“撇”;当k<0时,“捺”
当b>0时,图像与y轴交于正半轴;当b<0时,图像与y轴交于负半轴。
2、反比例函数y=k/x(k≠0): 当k>0时,函数图象在第一、三象限
当k<0时,函数图象在第二、四象限
【典型例题】
例1、已知 k1<0<k2,则函数 y=k1x 和 y= 的图象大致是( )
A B C D
【巩固练习】
1、在同一直角坐标系中,函数y=kx-k与y=(k≠0)的图象大致是( )
2、如图,函数y= 与y=kx+k在同一坐标系内的图像大致是( )
【题型二】
例、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数,其图象如图1所示.当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应( )
A.不小于m3 B.小于m3
C.不小于m3 D.小于m3
【巩固练习】
1、一块蓄电池的电压为定值,使用此蓄电池为电源时,电流(A)与电阻(Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过10A,那么此用电器的可变电阻应( )
A.不小于4.8Ω B.不大于4.8Ω
C.不小于14Ω D.不大于14Ω
2、 某汽车的功率P为一定值,汽车行驶时的速度v(米/秒)与它所受的牵引力F(牛)之间的函数关系如右图所示:
(1)这辆汽车的功率是多少?请写出这一函数的表达式;
(2)当它所受牵引力为1200牛时,汽车的速度为多少千米/时?
(3)如果限定汽车的速度不超过30米/秒,则F在什么范围内?
3、已知蓄电池的电压为定值,使用此电源时,
电流I(A)与电阻R(Ω)之间的函数关系如图所示:
1) 蓄电池的电压是多少?
2) 求这一函数的表达式;
3) 如果以此蓄电池为电源的用电器限制电 流
不得超过10A,那么用电器的可变电阻
应控制在什么范围内?
4、某校对教室采用药薰消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例;药物燃烧完后,y与x成反比例(如图所示)。现测得药物10min燃毕,此时室内空气中每立方米的含药量为8mg。请根据题中所提供的信息,解答下列问题:
1)药物燃烧时,y关于x的函数关系式为________,自变量的取值范围是________;药物燃烧后,y关于x的函数关系式为________。
2)研究表明,当空气中每立方米的含药量不超过2mg时,对人体没有影响,那么学校规定从消毒开始,至少要45分钟后,学生才能回到教室,学校的规定合理吗?
※3)研究表明,当空气中每立方米的含药量不低于4mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
解:
【题型三】面积问题
的几何含义:反比例函数y= (k≠0)中比例系数k的几何
意义,即过双曲线y= (k≠0)上任意一点P作x轴、y轴
垂线,设垂足分别为A、B,则所得矩形OAPB的面积为 .
【知识要点】
1、反比例函数图像中,求多边形面积常用到xy=k(变式)
2、求多边形面积时若不能直接求出,则需将所要求的多边形面积转化为几个多边形面积的和与差。
【典型例题】
例1、在直角坐标系中,点A是轴正半轴上的一个定点,点B是双曲线()上的一个动点,当点B的横坐标逐渐增大时,的面积将会( )
A.逐渐增大 B.不变 C.逐渐减小 D.先增大后减小
例2、如图,一次函数的图象与反比例函数的图象交于
两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求的面积.
【巩固练习】
1、如图,P是x轴上正半轴的一个动点,过点P作x轴的垂线PQ交双曲线于点Q,连结OQ,当P沿x轴的正方向运动时,RtΔQOP的面积( )
A 逐渐增大 B 逐渐减小 C 保持不变 D 无法确定
2、如图,在反比例函数()的图象上,有点P1、P2、P3、P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1、S2、S3,则①S1+S2+S3+S4= ;②S1+S2+S3 = 。
3、如图,在轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、 A3P4A4 、A4P5A5并设其面积分别为S1 S2 S3 S4 S5则S5的值为 .以此类推,则Sn=
4、反比例函数的图象与一次函数的图象交于,两点.
(1)求反比例函数与一次函数的解析式;
(2)求三角形AOB的面积
(3)根据图象回答:当取何值时,反比例函数的值大于一次函数的值.
5、如图正方形OABC的面积为4,点O为坐标原点,点B在函数
的图象上,点P(m,n)是函数的图象上异于B的任意一点,
过点P分别作x轴、y轴的垂线,垂足分别为E、F.
(1)设矩形OEPF的面积为Sl,
(2判断Sl与点P的位置是否有关(不必说理由).
(3)从矩形OEPF的面积中减去其与正方形OABC重合的面积,剩余面积记为S2,
写出S2与m的函数关系,并标明m的取值范
x
y
O
x
y
O
O
x
y
x
y
O
6
I/A
8
第1题图
·A(9,4)
R/Ω
I/A
y(mg)
X(min)
x
y
O
A
B
O
y
x
B
A
x
y
O
P1
P2
P3
P4
1
2
3
4
y
x
A
O
B
1
一、反比例函数定义
【知识要点】
一般地,如果两个变量x、y之间的关系可以表示成y= (k为常数,k≠0)的形式,那么称y是x的反比例函数.
【巩固练习】
1、已知反比例函数的图象经过点,则这个反比例函数的解析式是 .
2、近视眼镜的度数(度)与镜片焦距(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数与镜片焦距之间的函数关系式为 .
二、 反比例函数的图象和性质
【知识要点】
【题型一】象限与点
1、反比例函数(m-1)的图象在第二、四象限,则m=
2、点(5,-6)在反比例函数的图像上,那么k=_________,该反比例函数的图像位于第_______象限.
3、如果双曲线y=经过点(-2,3),那么此双曲线也经过点
(A)(-2,-3) (B)(3,2) (C)(3,-2) (D)(-3,-2)
4、如果反比例函数的图像经过点(-3,),那么直线y=kx-k一定经过点(—2,___).
【题型二】增减性问题
当k>0时,函数图象在第一、三象限,y随x的增大而减小
当k<0时,函数图象在第二、四象限,y随x的增大而增大
【典型例题】
例1:已知点A()、B()是反比例函数()图象上的两点,若,则有( )
A. B. C. D.
【巩固练习】
1、在反比例函数图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是 ( )
A.k>3 B.k>0 C.k<3 D. k<0
2、已知(x1,y1),(x2,y2)为反比例函数图象上的点,当x1<x2<0时,y1<y2,则k的值可
为 (写一个即可)
3、在函数 y=(k<0)的图象上有A(1,y1)、B(-1,y2)、C(-2,y3)三个点,则下列各式中正确( )
A、y1<y2<y3 B、y1<y3<y2 C、y3<y2<y1 D、y2<y3<y1
三、反比例函数应用
【题型一】图像问题
1、一次函数y=kx+b:当k>0时,“撇”;当k<0时,“捺”
当b>0时,图像与y轴交于正半轴;当b<0时,图像与y轴交于负半轴。
2、反比例函数y=k/x(k≠0): 当k>0时,函数图象在第一、三象限
当k<0时,函数图象在第二、四象限
【典型例题】
例1、已知 k1<0<k2,则函数 y=k1x 和 y= 的图象大致是( )
A B C D
【巩固练习】
1、在同一直角坐标系中,函数y=kx-k与y=(k≠0)的图象大致是( )
2、如图,函数y= 与y=kx+k在同一坐标系内的图像大致是( )
【题型二】
例、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数,其图象如图1所示.当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应( )
A.不小于m3 B.小于m3
C.不小于m3 D.小于m3
【巩固练习】
1、一块蓄电池的电压为定值,使用此蓄电池为电源时,电流(A)与电阻(Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过10A,那么此用电器的可变电阻应( )
A.不小于4.8Ω B.不大于4.8Ω
C.不小于14Ω D.不大于14Ω
2、 某汽车的功率P为一定值,汽车行驶时的速度v(米/秒)与它所受的牵引力F(牛)之间的函数关系如右图所示:
(1)这辆汽车的功率是多少?请写出这一函数的表达式;
(2)当它所受牵引力为1200牛时,汽车的速度为多少千米/时?
(3)如果限定汽车的速度不超过30米/秒,则F在什么范围内?
3、已知蓄电池的电压为定值,使用此电源时,
电流I(A)与电阻R(Ω)之间的函数关系如图所示:
1) 蓄电池的电压是多少?
2) 求这一函数的表达式;
3) 如果以此蓄电池为电源的用电器限制电 流
不得超过10A,那么用电器的可变电阻
应控制在什么范围内?
4、某校对教室采用药薰消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例;药物燃烧完后,y与x成反比例(如图所示)。现测得药物10min燃毕,此时室内空气中每立方米的含药量为8mg。请根据题中所提供的信息,解答下列问题:
1)药物燃烧时,y关于x的函数关系式为________,自变量的取值范围是________;药物燃烧后,y关于x的函数关系式为________。
2)研究表明,当空气中每立方米的含药量不超过2mg时,对人体没有影响,那么学校规定从消毒开始,至少要45分钟后,学生才能回到教室,学校的规定合理吗?
※3)研究表明,当空气中每立方米的含药量不低于4mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
解:
【题型三】面积问题
的几何含义:反比例函数y= (k≠0)中比例系数k的几何
意义,即过双曲线y= (k≠0)上任意一点P作x轴、y轴
垂线,设垂足分别为A、B,则所得矩形OAPB的面积为 .
【知识要点】
1、反比例函数图像中,求多边形面积常用到xy=k(变式)
2、求多边形面积时若不能直接求出,则需将所要求的多边形面积转化为几个多边形面积的和与差。
【典型例题】
例1、在直角坐标系中,点A是轴正半轴上的一个定点,点B是双曲线()上的一个动点,当点B的横坐标逐渐增大时,的面积将会( )
A.逐渐增大 B.不变 C.逐渐减小 D.先增大后减小
例2、如图,一次函数的图象与反比例函数的图象交于
两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求的面积.
【巩固练习】
1、如图,P是x轴上正半轴的一个动点,过点P作x轴的垂线PQ交双曲线于点Q,连结OQ,当P沿x轴的正方向运动时,RtΔQOP的面积( )
A 逐渐增大 B 逐渐减小 C 保持不变 D 无法确定
2、如图,在反比例函数()的图象上,有点P1、P2、P3、P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1、S2、S3,则①S1+S2+S3+S4= ;②S1+S2+S3 = 。
3、如图,在轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、 A3P4A4 、A4P5A5并设其面积分别为S1 S2 S3 S4 S5则S5的值为 .以此类推,则Sn=
4、反比例函数的图象与一次函数的图象交于,两点.
(1)求反比例函数与一次函数的解析式;
(2)求三角形AOB的面积
(3)根据图象回答:当取何值时,反比例函数的值大于一次函数的值.
5、如图正方形OABC的面积为4,点O为坐标原点,点B在函数
的图象上,点P(m,n)是函数的图象上异于B的任意一点,
过点P分别作x轴、y轴的垂线,垂足分别为E、F.
(1)设矩形OEPF的面积为Sl,
(2判断Sl与点P的位置是否有关(不必说理由).
(3)从矩形OEPF的面积中减去其与正方形OABC重合的面积,剩余面积记为S2,
写出S2与m的函数关系,并标明m的取值范
x
y
O
x
y
O
O
x
y
x
y
O
6
I/A
8
第1题图
·A(9,4)
R/Ω
I/A
y(mg)
X(min)
x
y
O
A
B
O
y
x
B
A
x
y
O
P1
P2
P3
P4
1
2
3
4
y
x
A
O
B
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
