2018-2019学年黑龙江省哈尔滨市南岗区虹桥中学九年级(下)开学数学试卷解析版
文档属性
| 名称 | 2018-2019学年黑龙江省哈尔滨市南岗区虹桥中学九年级(下)开学数学试卷解析版 | 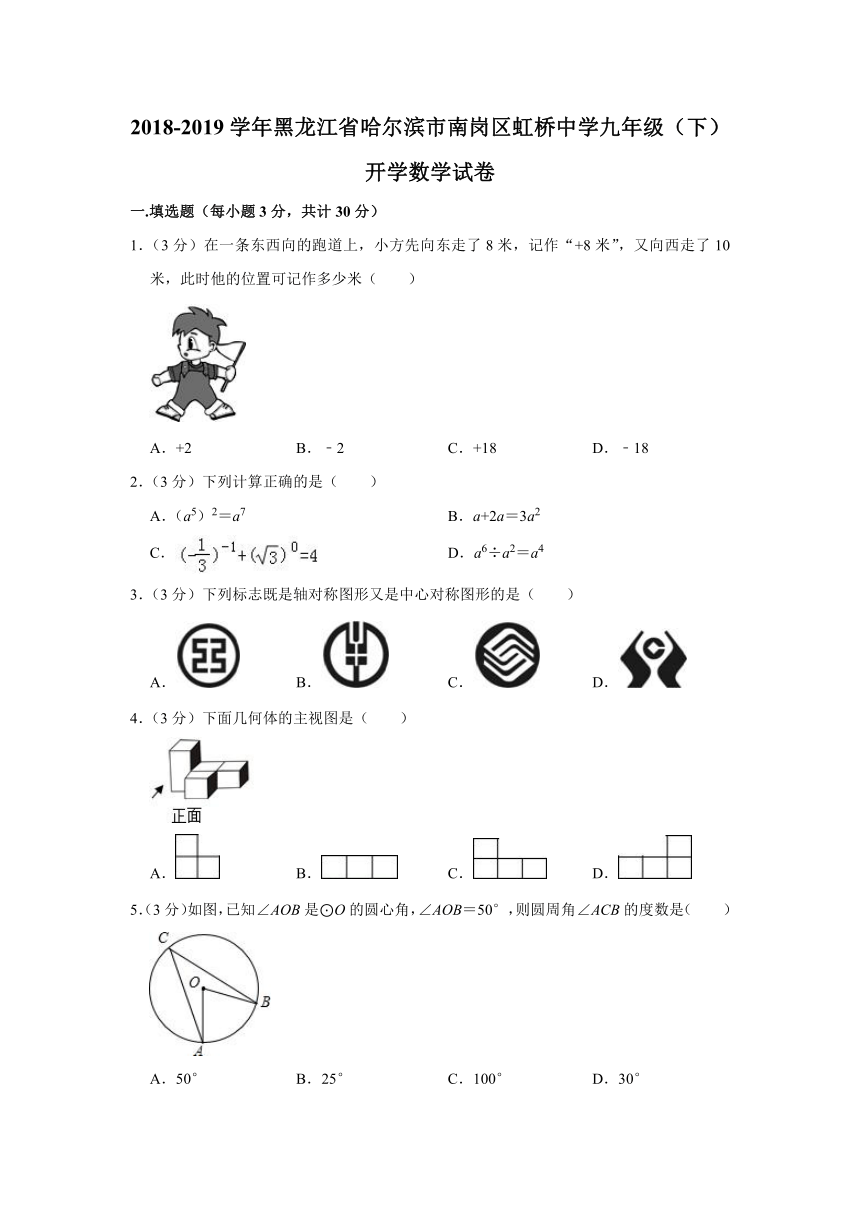 | |
| 格式 | zip | ||
| 文件大小 | 203.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-29 07:09:56 | ||
图片预览




文档简介
2018-2019学年黑龙江省哈尔滨市南岗区虹桥中学九年级(下)开学数学试卷
一.填选题(每小题3分,共计30分)
1.(3分)在一条东西向的跑道上,小方先向东走了8米,记作“+8米”,又向西走了10米,此时他的位置可记作多少米( )
A.+2 B.﹣2 C.+18 D.﹣18
2.(3分)下列计算正确的是( )
A.(a5)2=a7 B.a+2a=3a2
C. D.a6÷a2=a4
3.(3分)下列标志既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.(3分)下面几何体的主视图是( )
A. B. C. D.
5.(3分)如图,已知∠AOB是⊙O的圆心角,∠AOB=50°,则圆周角∠ACB的度数是( )
A.50° B.25° C.100° D.30°
6.(3分)把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A.y=﹣(x﹣1)2﹣3 B.y=﹣(x+1)2﹣3
C.y=﹣(x﹣1)2+3 D.y=﹣(x+1)2+3
7.(3分)反比例函数的图象在每个象限内,y随x的增大而增大,则a的取值范围是( )
A.a≥﹣3 B.a>﹣3 C.a≤﹣3 D.a<﹣3
8.(3分)如图,CD为⊙O的直径,且CD⊥弦AB,∠AOC=50°,则∠B大小为( )
A.25° B.30° C.40° D.65°
9.(3分)在△ABC中,已知∠C=90°,BC=4,sinA=,那么AC边的长是( )
A.6 B.2 C.3 D.2
10.(3分)如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
A.= B.= C.= D.=
二、填空题(每小题3分,共计30分)
11.(3分)2018年中央预算用于教育、医疗卫生、社会保障、就业等方面的民生支出达到7300亿元,用科学记数法表示为 元.
12.(3分)分解因式:ax2﹣4ax+4a= .
13.(3分)计算:+= .
14.(3分)分式方程的解为:x= .
15.(3分)“五一”期间,某服装商店举行促销活动,全部商品八折销售,小华购买一件原价为140元的运动服,打折后他比按原价购买节省了 元.
16.(3分)二次函数y=x2﹣6x+1的图象的顶点坐标是 .
17.(3分)在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是 .
18.(3分)已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆心角为 .
19.(3分)等边△ABC所在平面内有一点D,BD=2、CD=4、且∠BDC=120°,射线BD交直线AC于点E,则AE= .
20.(3分)在△ABC中,AB=2,BC=3,tan∠ABC=2,以AC为腰的等腰△ADC中,AC=AD,且tan∠ADC=,连接BD.则BD的长为 .
三、解答题(其中21、22题各7分,23、24题各8分,25题-27题各10分,共60分)
21.(7分)先化简,再求值:÷﹣,其中x=2tan60°﹣4sin30°.
22.(7分)图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A、B在小正方形的顶点上、
(1)在图1中画出△ABC(点C在小正方形的顶点上),△ABC的面积为5.且△ABC中有一个角为45°(画一个即可)
(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD的面积为5,且∠ADB=90°(画一个即可).
23.(8分)某校课题研究小组对本校九年级全体同学体育测试情况进行调查,他们随机抽查部分同学体育测试成绩(由高到低分A、B、C、D四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该课题研究小组共抽查了 名同学的体育测试成绩,扇形统计图中B级所占的百分比b= ;
(2)补全条形统计图;
(3)若该校九年级共有400名同学,请估计该校九年级同学体育测试达标(测试成绩C级以上,含C级)约有 名.
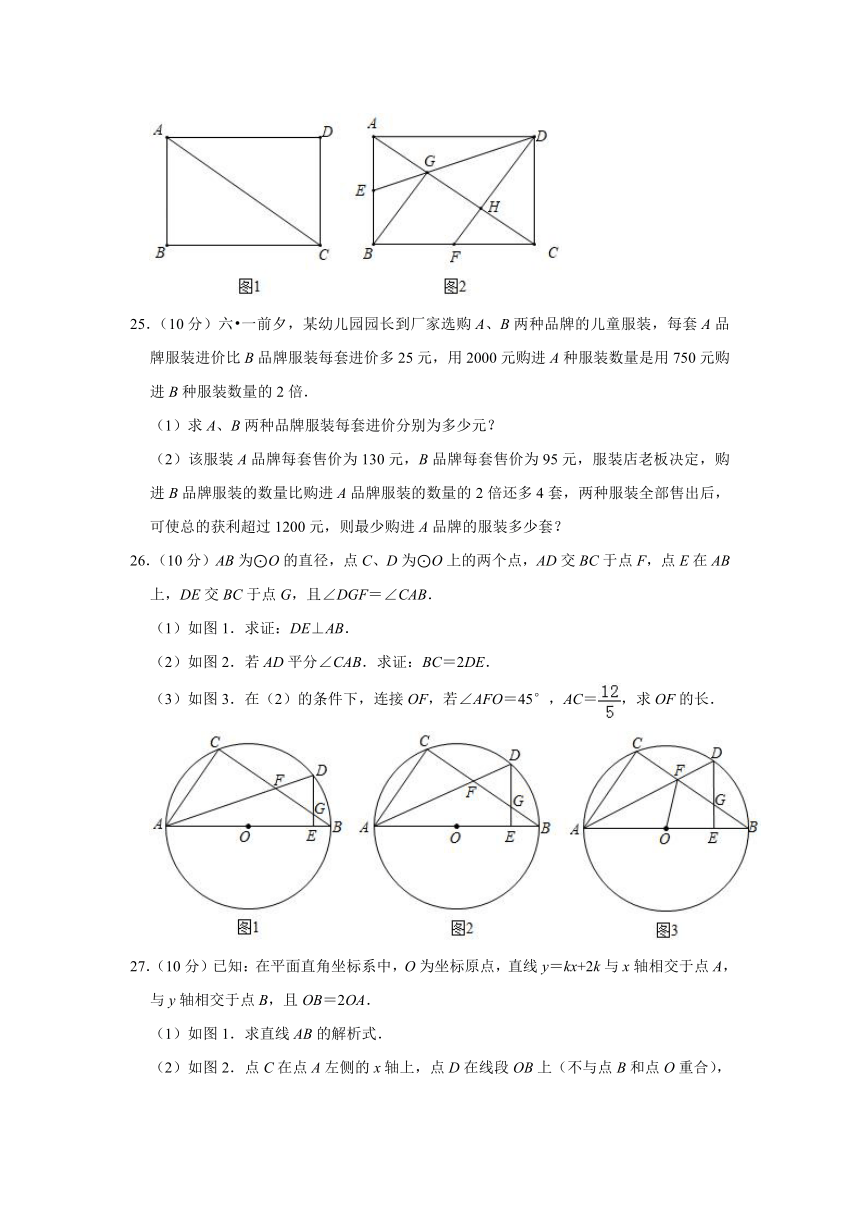
24.(8分)已知:四边形ABCD中,AC为对角线,∠DAC=∠BCA,且AD=BC,CD⊥AD于点D.
(1)如图1,求证:四边形ABCD是矩形.
(2)如图2,点E和点F分别为边AB和边BC的中点,连接DE、DF分别交AC于点G和点H,连接BG,在不连接其它线段的情况下,请写出所有面积是△FHC面积的2倍的所有三角形.
25.(10分)六?一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
(1)求A、B两种品牌服装每套进价分别为多少元?
(2)该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
26.(10分)AB为⊙O的直径,点C、D为⊙O上的两个点,AD交BC于点F,点E在AB上,DE交BC于点G,且∠DGF=∠CAB.
(1)如图1.求证:DE⊥AB.
(2)如图2.若AD平分∠CAB.求证:BC=2DE.
(3)如图3.在(2)的条件下,连接OF,若∠AFO=45°,AC=,求OF的长.
27.(10分)已知:在平面直角坐标系中,O为坐标原点,直线y=kx+2k与x轴相交于点A,与y轴相交于点B,且OB=2OA.
(1)如图1.求直线AB的解析式.
(2)如图2.点C在点A左侧的x轴上,点D在线段OB上(不与点B和点O重合),CD交AB于点E,且tan∠DCO=,设点E的横坐标为t,△ACE的面积为s,求s与t之间的函数关系式.
(3)如图3,当s=5时,过点C作CF∥AB交y轴于点F,过点E作EG⊥CD交CF于点G,求点G的坐标.
2018-2019学年黑龙江省哈尔滨市南岗区虹桥中学九年级(下)开学数学试卷
参考答案与试题解析
一.填选题(每小题3分,共计30分)
1.【解答】解:∵“正”和“负”相对,小方先向东走了8米,记作“+8米”,
∴向西走了10米,记作﹣10米.
∴+8+(﹣10)=﹣2.
故选:B.
2.【解答】解:A、(a5)2=a10,故本选项错误;
B、a+2a=3a,故本选项错误;
C、﹣3+1=﹣2,故本选项错误;
D、a6÷a2=a4,故本选项正确;
故选:D.
3.【解答】解:A、是轴对称图形,是中心对称图形.故正确;
B、是轴对称图形,不是中心对称图形.故错误;
C、不是轴对称图形,是中心对称图形.故错误;
D、是轴对称图形,不是中心对称图形.故错误.
故选:A.
4.【解答】解:如图所示:.
故选:C.
5.【解答】解:∵∠AOB=50°,
∴∠ACB=∠AOB=25°.
故选:B.
6.【解答】解:当y=﹣x2向左平移1个单位时,顶点由原来的(0,0)变为(﹣1,0),
当向上平移3个单位时,顶点变为(﹣1,3),
则平移后抛物线的解析式为y=﹣(x+1)2+3.
故选:D.
7.【解答】解:∵反比例函数的图象在每个象限内,y随x的增大而增大,
∴a+3<0,解得a<﹣3.
故选:D.
8.【解答】解:∵CD⊥AB,
∴,
∴∠D=∠AOC=25°,
∴∠B=90°﹣25°=65°;
故选:D.
9.【解答】解:∵在△ABC中,∠C=90°,BC=4,
∴sinA===,
∴AB=6.
∴AC==2.
故选:B.
10.【解答】解:(A)∵DE∥BC,
∴△ADE∽△ABC,
∴,故A错误;
(B)∵DE∥BC,
∴,故B错误;
(C)∵DE∥BC,
,故C正确;
(D)∵DE∥BC,
∴△AGE∽△AFC,
∴=,故D错误;
故选:C.
二、填空题(每小题3分,共计30分)
11.【解答】解:7300亿=7.3×1011,
故答案为:7.3×1011.
12.【解答】解:ax2﹣4ax+4a,
=a(x2﹣4x+4),
=a(x﹣2)2.
13.【解答】解:原式=2+3=;
故答案为:5.
14.【解答】解:方程两边同乘以(x﹣3)(x﹣1),
得x(x﹣1)=(x﹣3)(x+1),
解得x=﹣3,
将x=﹣3代入(x﹣3)(x﹣1)=24≠0,
所以原方程的解为:x=﹣3.
15.【解答】解:根据题意,节省了140×(1﹣80%)=28元.
16.【解答】解:∵y=x2﹣6x+1=(x﹣3)2﹣8,
∴抛物线顶点坐标为(3,﹣8).
故答案为:(3,﹣8).
17.【解答】解:
∴一共有12种情况,有2种情况两次都摸到红球,
∴两次都摸到红球的概率是 =.
故答案为.
18.【解答】解:∵l=,
∴n=,
故答案为:160°.
19.【解答】解:①当点D在△ABC外部时,如图1.
将线段BD绕点B逆时针旋转60°到BD',连接DD',AD',DD'与BC交于点G.
∵∠D'BD=60°,BD=BD',
∴△BDD'为等边三角形,
∴BD=BD'=DD'=2,∠BD'D=∠D'BD=BDD'=60°,
∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=∠BAC=60°,
∴∠ABC=D'BD,
∴∠ABD'=∠CBD,
∴△ABD'≌△CBD(SAS),
∴∠AD'B=∠CDB=120°,AD'=CD=4,
∴∠AD'B+BD'D=180°,
∴点A、D'、D在同一直线上,
∵∠D'BD+∠BDC=180°,
∴BD'∥CD,
△BD'G∽△CDG,
∴,
∴D'G=DG,
∵DD'=2,
∴D'G=,DG=,
∴AG=AD'+D'G=4+=,
在△ABG与△ADB中,∠ABG=∠ADB=60°,∠BAD=GAB,
∴△ABG∽△ADB,
∴,
AB2=AD?AG=(AD'+DD')?AG=(4+2)×=28,
∴AB=2,AC=BC=
在△BCE与△BDC中,
∠BCE=∠BDC=120°,∠BEC=∠BCD,
∴△BCE∽△BDC,
∴,,
∴CE=4,
∴AE=AC+CE=2+4=6
②当点D在△ABC内部时,如图2.
将线段BD绕点B逆时针旋转60°到BD',连接DD'、AD'.
∵∠D'BD=60°,BD=BD',
∴△BDD'为等边三角形,
∴BD=BD'=DD'=2,∠BD'D=∠D'BD=BDD'=60°,
∴∠BDC+BDD'=180°,
∴点B、D、E在同一直线上,
∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=∠BAC=60°,
∴∠ABC=D'BD,
∴∠ABD'=∠CBD,
∵BD'=BD=2,BA=BC
∴△ABD'≌△CBD(SAS),
∴∠AD'B=∠CDB=120°,AD'=CD=4,CD'=CD+DD'=4+2=6,
∴∠AD'B+∠D'BD=180°,
∴BD∥AD',
∴△CDE∽△CD'A,
∴,
,DE=,
∴BE=BD+DE=2+=,
在△EDC与ECB中,
∵∠EDC=180°﹣∠BDC=180°﹣120°=60°=∠ECB,∠DEC=∠CEB,
∴△EDC∽ECB,
∴,
EC2=ED?EB==,
EC=,
∵DE∥AD',
∴,
,
∴AE=.
故答案为.
20.【解答】解:作AE⊥BC于E,AH⊥CD于H,作∠PAB=∠DCB,∠PBA=∠DBC,PG⊥BD,
∵AB=2,tan∠ABC=2,
∴tan∠ABC==2,
∴AE=2BE,
∵AB2=AE2+BE2,即(2)2=5BE2,
∴BE=2,
∴AE=4,EC=BC﹣BE=3﹣2=1,
∴AC==,
∵AC=AD,
∴AD=,DH=HC=DC,
∵tan∠ADC=,
∴tan∠ADC==,
∴DH=2AH,
∵AD2=AH2+DH2,即17=5AH2,
∴AH=,
∴DC=4AH=,
作∠PAB=∠DCB,∠PBA=∠DBC,PG⊥BD,
∴△PAB∽△DBC;
∴
∴,
∴PA=,
∵tan∠ABC=2,tan∠ADC=,
∴∠ABC+∠ADC=90°,
∴∠BCD+∠BAD=270°,,
∴∠PAD=360°﹣270°=90°,
∴PD==,
∵∠PAB=∠DCB,
∴∠PAD=∠ABC,
∴,
∴△PBD∽△ABC,
∴;
∴,
∴BD=
三、解答题(其中21、22题各7分,23、24题各8分,25题-27题各10分,共60分)
21.【解答】解:÷﹣
=
=
=,
当x=2tan60°﹣4sin30°=2﹣4×=2时,原式=.
22.【解答】解:
23.【解答】解:读图可知:
(1)A级有20人,占25%,则共抽查了:20÷25%=80(人);
B级占1﹣25%﹣30%﹣5%=40%;
(2)C级占30%,有80×30%=24(人).如图:
(3)80人中,有20+37+24=76(人)达标,据此可推测九年级共有400名同学,应有400×=380(人)达标.
24.【解答】(1)证明:∵∠DAC=∠BCA,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∵CD⊥AD,
∴∠D=90°,
∴?ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AB=CD,
∵点E和点F分别为边AB和边BC的中点,
∴AB=CD=2AE,AD=BC=2CF,
∵AD∥BC,AB∥CD,
∴△AEG∽△CDG,△CFH∽△ADH,
∴,==,
∴==,S△CDH=2S△CHF,
∴AG=GH=CH,
∴S△ADG=S△DGH=S△CDH,
在△ABG与△CDH中,,
∴△ABG≌△CDH(SAS),
∴S△ABG=S△CDH,
∴S△ADG=S△DGH=S△CDH=S△ABG=2S△CHF,
∴面积是△FHC面积的2倍的所有三角形是△ADG,△DGH,△CDH,△ABG.
25.【解答】解:(1)设A品牌服装每套进价为x元,则B品牌服装每套进价为(x﹣25)元,由题意得:
=×2,
解得:x=100,
经检验:x=100是原分式方程的解,
x﹣25=100﹣25=75,
答:A、B两种品牌服装每套进价分别为100元、75元;
(2)设购进A品牌的服装a套,则购进B品牌服装(2a+4)套,由题意得:
(130﹣100)a+(95﹣75)(2a+4)>1200,
解得:a>16,
答:至少购进A品牌服装的数量是17套.
26.【解答】解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵∠DGF=∠CAB,∠DGF=∠BGE,
∴∠BGE=∠CAB,
∴∠BGE+∠CBA=90°,
∴∠GEB=90°,
∴DE⊥AB;
(2)如图2,连接OD交BC于H,连接BD,
∵AD平分∠CAB,
∴,
∴OD⊥BC,BH=CH,
∵DE⊥AB,OD=OB,
∴S△OBD=OD×BH=OB×DE,
∴BH=DE,
∴BC=2DE.
(3)如图3,作FR⊥AB于R,OS⊥AD于S,
∵AD平分∠CAB,
∴∠CAD=∠BAD=x,
∴∠FBO=90°﹣2x,
∵∠AFO=45°,
∴∠FOB=45°+x,
∴∠OFB=180°﹣(90°﹣2x)﹣(45°+x)=45°+x,
∴∠FOB=∠OFB
∴BF=BO=OA,
∵∠FRB=∠ACB=90°,∠FBR=∠ABC,
∴△BFR∽△BAC,
∴,
∵AC=,
∴FR=,
∴CF=FR=,
∴AF=,tan∠FAR=tan∠FAC=,
设SO=t,AS=2t,SF=SO=t,
则AF=AS+SF=3t=,t=,
∴OF=t=.
27.【解答】解:(1)设A(a,0)(a<0)
∴OB=2OA=﹣2a,即B(0,﹣2a)
∵直线y=kx+2k过点A、B
∴ 解得:
∴直线AB的解析式为:y=2x+4
(2)过点E作EH⊥x轴于点H,
由(1)可得A(﹣2,0)
∵E在线段AB上,xE=t
∴﹣2<t<0,OH=﹣t,EH=yE=2t+4
∵在Rt△CEH中,tan∠DCO=
∴CH=3EH=6t+12
∴CO=CH+HO=6t+12﹣t=5t+12
CA=CO﹣AO=5t+12﹣2=5t+10
∴S=AC?EH=(5t+10)(2t+4)=5t2+20t+20
(3)过G作GM⊥y轴于点M,过E作EN⊥GM于点N,过E作EP∥x轴
∴∠PEC=∠DCO,∠PEN=90°
∵EG⊥CD
∴∠CEG=90°,即∠CEG=∠PEN
∴∠CEG﹣∠PEG=∠PEN﹣∠PEG
即∠PEC=∠GEN=∠DCO
∴tan∠DCO=tan∠GEN=
∵S=5时,5t2+20t+20=5,解得:t1=﹣1,t2=﹣3(舍去)
∴E(﹣1,2),CO=5t+12=7
∴C(﹣7,0)
∵CF∥AB,设直线CF解析式为y=2x+b
2×(﹣7)+b=0 解得:b=14
∴直线CF解析式为y=2x+14
设G(m,2m+14)(﹣7<m<0)
∴GN=﹣1﹣m,NE=2m+14﹣2=2m+12
∴
解得:m=﹣3
∴G(﹣3,8)
一.填选题(每小题3分,共计30分)
1.(3分)在一条东西向的跑道上,小方先向东走了8米,记作“+8米”,又向西走了10米,此时他的位置可记作多少米( )
A.+2 B.﹣2 C.+18 D.﹣18
2.(3分)下列计算正确的是( )
A.(a5)2=a7 B.a+2a=3a2
C. D.a6÷a2=a4
3.(3分)下列标志既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.(3分)下面几何体的主视图是( )
A. B. C. D.
5.(3分)如图,已知∠AOB是⊙O的圆心角,∠AOB=50°,则圆周角∠ACB的度数是( )
A.50° B.25° C.100° D.30°
6.(3分)把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A.y=﹣(x﹣1)2﹣3 B.y=﹣(x+1)2﹣3
C.y=﹣(x﹣1)2+3 D.y=﹣(x+1)2+3
7.(3分)反比例函数的图象在每个象限内,y随x的增大而增大,则a的取值范围是( )
A.a≥﹣3 B.a>﹣3 C.a≤﹣3 D.a<﹣3
8.(3分)如图,CD为⊙O的直径,且CD⊥弦AB,∠AOC=50°,则∠B大小为( )
A.25° B.30° C.40° D.65°
9.(3分)在△ABC中,已知∠C=90°,BC=4,sinA=,那么AC边的长是( )
A.6 B.2 C.3 D.2
10.(3分)如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
A.= B.= C.= D.=
二、填空题(每小题3分,共计30分)
11.(3分)2018年中央预算用于教育、医疗卫生、社会保障、就业等方面的民生支出达到7300亿元,用科学记数法表示为 元.
12.(3分)分解因式:ax2﹣4ax+4a= .
13.(3分)计算:+= .
14.(3分)分式方程的解为:x= .
15.(3分)“五一”期间,某服装商店举行促销活动,全部商品八折销售,小华购买一件原价为140元的运动服,打折后他比按原价购买节省了 元.
16.(3分)二次函数y=x2﹣6x+1的图象的顶点坐标是 .
17.(3分)在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是 .
18.(3分)已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆心角为 .
19.(3分)等边△ABC所在平面内有一点D,BD=2、CD=4、且∠BDC=120°,射线BD交直线AC于点E,则AE= .
20.(3分)在△ABC中,AB=2,BC=3,tan∠ABC=2,以AC为腰的等腰△ADC中,AC=AD,且tan∠ADC=,连接BD.则BD的长为 .
三、解答题(其中21、22题各7分,23、24题各8分,25题-27题各10分,共60分)
21.(7分)先化简,再求值:÷﹣,其中x=2tan60°﹣4sin30°.
22.(7分)图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A、B在小正方形的顶点上、
(1)在图1中画出△ABC(点C在小正方形的顶点上),△ABC的面积为5.且△ABC中有一个角为45°(画一个即可)
(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD的面积为5,且∠ADB=90°(画一个即可).
23.(8分)某校课题研究小组对本校九年级全体同学体育测试情况进行调查,他们随机抽查部分同学体育测试成绩(由高到低分A、B、C、D四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该课题研究小组共抽查了 名同学的体育测试成绩,扇形统计图中B级所占的百分比b= ;
(2)补全条形统计图;
(3)若该校九年级共有400名同学,请估计该校九年级同学体育测试达标(测试成绩C级以上,含C级)约有 名.
24.(8分)已知:四边形ABCD中,AC为对角线,∠DAC=∠BCA,且AD=BC,CD⊥AD于点D.
(1)如图1,求证:四边形ABCD是矩形.
(2)如图2,点E和点F分别为边AB和边BC的中点,连接DE、DF分别交AC于点G和点H,连接BG,在不连接其它线段的情况下,请写出所有面积是△FHC面积的2倍的所有三角形.
25.(10分)六?一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
(1)求A、B两种品牌服装每套进价分别为多少元?
(2)该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
26.(10分)AB为⊙O的直径,点C、D为⊙O上的两个点,AD交BC于点F,点E在AB上,DE交BC于点G,且∠DGF=∠CAB.
(1)如图1.求证:DE⊥AB.
(2)如图2.若AD平分∠CAB.求证:BC=2DE.
(3)如图3.在(2)的条件下,连接OF,若∠AFO=45°,AC=,求OF的长.
27.(10分)已知:在平面直角坐标系中,O为坐标原点,直线y=kx+2k与x轴相交于点A,与y轴相交于点B,且OB=2OA.
(1)如图1.求直线AB的解析式.
(2)如图2.点C在点A左侧的x轴上,点D在线段OB上(不与点B和点O重合),CD交AB于点E,且tan∠DCO=,设点E的横坐标为t,△ACE的面积为s,求s与t之间的函数关系式.
(3)如图3,当s=5时,过点C作CF∥AB交y轴于点F,过点E作EG⊥CD交CF于点G,求点G的坐标.
2018-2019学年黑龙江省哈尔滨市南岗区虹桥中学九年级(下)开学数学试卷
参考答案与试题解析
一.填选题(每小题3分,共计30分)
1.【解答】解:∵“正”和“负”相对,小方先向东走了8米,记作“+8米”,
∴向西走了10米,记作﹣10米.
∴+8+(﹣10)=﹣2.
故选:B.
2.【解答】解:A、(a5)2=a10,故本选项错误;
B、a+2a=3a,故本选项错误;
C、﹣3+1=﹣2,故本选项错误;
D、a6÷a2=a4,故本选项正确;
故选:D.
3.【解答】解:A、是轴对称图形,是中心对称图形.故正确;
B、是轴对称图形,不是中心对称图形.故错误;
C、不是轴对称图形,是中心对称图形.故错误;
D、是轴对称图形,不是中心对称图形.故错误.
故选:A.
4.【解答】解:如图所示:.
故选:C.
5.【解答】解:∵∠AOB=50°,
∴∠ACB=∠AOB=25°.
故选:B.
6.【解答】解:当y=﹣x2向左平移1个单位时,顶点由原来的(0,0)变为(﹣1,0),
当向上平移3个单位时,顶点变为(﹣1,3),
则平移后抛物线的解析式为y=﹣(x+1)2+3.
故选:D.
7.【解答】解:∵反比例函数的图象在每个象限内,y随x的增大而增大,
∴a+3<0,解得a<﹣3.
故选:D.
8.【解答】解:∵CD⊥AB,
∴,
∴∠D=∠AOC=25°,
∴∠B=90°﹣25°=65°;
故选:D.
9.【解答】解:∵在△ABC中,∠C=90°,BC=4,
∴sinA===,
∴AB=6.
∴AC==2.
故选:B.
10.【解答】解:(A)∵DE∥BC,
∴△ADE∽△ABC,
∴,故A错误;
(B)∵DE∥BC,
∴,故B错误;
(C)∵DE∥BC,
,故C正确;
(D)∵DE∥BC,
∴△AGE∽△AFC,
∴=,故D错误;
故选:C.
二、填空题(每小题3分,共计30分)
11.【解答】解:7300亿=7.3×1011,
故答案为:7.3×1011.
12.【解答】解:ax2﹣4ax+4a,
=a(x2﹣4x+4),
=a(x﹣2)2.
13.【解答】解:原式=2+3=;
故答案为:5.
14.【解答】解:方程两边同乘以(x﹣3)(x﹣1),
得x(x﹣1)=(x﹣3)(x+1),
解得x=﹣3,
将x=﹣3代入(x﹣3)(x﹣1)=24≠0,
所以原方程的解为:x=﹣3.
15.【解答】解:根据题意,节省了140×(1﹣80%)=28元.
16.【解答】解:∵y=x2﹣6x+1=(x﹣3)2﹣8,
∴抛物线顶点坐标为(3,﹣8).
故答案为:(3,﹣8).
17.【解答】解:
∴一共有12种情况,有2种情况两次都摸到红球,
∴两次都摸到红球的概率是 =.
故答案为.
18.【解答】解:∵l=,
∴n=,
故答案为:160°.
19.【解答】解:①当点D在△ABC外部时,如图1.
将线段BD绕点B逆时针旋转60°到BD',连接DD',AD',DD'与BC交于点G.
∵∠D'BD=60°,BD=BD',
∴△BDD'为等边三角形,
∴BD=BD'=DD'=2,∠BD'D=∠D'BD=BDD'=60°,
∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=∠BAC=60°,
∴∠ABC=D'BD,
∴∠ABD'=∠CBD,
∴△ABD'≌△CBD(SAS),
∴∠AD'B=∠CDB=120°,AD'=CD=4,
∴∠AD'B+BD'D=180°,
∴点A、D'、D在同一直线上,
∵∠D'BD+∠BDC=180°,
∴BD'∥CD,
△BD'G∽△CDG,
∴,
∴D'G=DG,
∵DD'=2,
∴D'G=,DG=,
∴AG=AD'+D'G=4+=,
在△ABG与△ADB中,∠ABG=∠ADB=60°,∠BAD=GAB,
∴△ABG∽△ADB,
∴,
AB2=AD?AG=(AD'+DD')?AG=(4+2)×=28,
∴AB=2,AC=BC=
在△BCE与△BDC中,
∠BCE=∠BDC=120°,∠BEC=∠BCD,
∴△BCE∽△BDC,
∴,,
∴CE=4,
∴AE=AC+CE=2+4=6
②当点D在△ABC内部时,如图2.
将线段BD绕点B逆时针旋转60°到BD',连接DD'、AD'.
∵∠D'BD=60°,BD=BD',
∴△BDD'为等边三角形,
∴BD=BD'=DD'=2,∠BD'D=∠D'BD=BDD'=60°,
∴∠BDC+BDD'=180°,
∴点B、D、E在同一直线上,
∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=∠BAC=60°,
∴∠ABC=D'BD,
∴∠ABD'=∠CBD,
∵BD'=BD=2,BA=BC
∴△ABD'≌△CBD(SAS),
∴∠AD'B=∠CDB=120°,AD'=CD=4,CD'=CD+DD'=4+2=6,
∴∠AD'B+∠D'BD=180°,
∴BD∥AD',
∴△CDE∽△CD'A,
∴,
,DE=,
∴BE=BD+DE=2+=,
在△EDC与ECB中,
∵∠EDC=180°﹣∠BDC=180°﹣120°=60°=∠ECB,∠DEC=∠CEB,
∴△EDC∽ECB,
∴,
EC2=ED?EB==,
EC=,
∵DE∥AD',
∴,
,
∴AE=.
故答案为.
20.【解答】解:作AE⊥BC于E,AH⊥CD于H,作∠PAB=∠DCB,∠PBA=∠DBC,PG⊥BD,
∵AB=2,tan∠ABC=2,
∴tan∠ABC==2,
∴AE=2BE,
∵AB2=AE2+BE2,即(2)2=5BE2,
∴BE=2,
∴AE=4,EC=BC﹣BE=3﹣2=1,
∴AC==,
∵AC=AD,
∴AD=,DH=HC=DC,
∵tan∠ADC=,
∴tan∠ADC==,
∴DH=2AH,
∵AD2=AH2+DH2,即17=5AH2,
∴AH=,
∴DC=4AH=,
作∠PAB=∠DCB,∠PBA=∠DBC,PG⊥BD,
∴△PAB∽△DBC;
∴
∴,
∴PA=,
∵tan∠ABC=2,tan∠ADC=,
∴∠ABC+∠ADC=90°,
∴∠BCD+∠BAD=270°,,
∴∠PAD=360°﹣270°=90°,
∴PD==,
∵∠PAB=∠DCB,
∴∠PAD=∠ABC,
∴,
∴△PBD∽△ABC,
∴;
∴,
∴BD=
三、解答题(其中21、22题各7分,23、24题各8分,25题-27题各10分,共60分)
21.【解答】解:÷﹣
=
=
=,
当x=2tan60°﹣4sin30°=2﹣4×=2时,原式=.
22.【解答】解:
23.【解答】解:读图可知:
(1)A级有20人,占25%,则共抽查了:20÷25%=80(人);
B级占1﹣25%﹣30%﹣5%=40%;
(2)C级占30%,有80×30%=24(人).如图:
(3)80人中,有20+37+24=76(人)达标,据此可推测九年级共有400名同学,应有400×=380(人)达标.
24.【解答】(1)证明:∵∠DAC=∠BCA,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∵CD⊥AD,
∴∠D=90°,
∴?ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AB=CD,
∵点E和点F分别为边AB和边BC的中点,
∴AB=CD=2AE,AD=BC=2CF,
∵AD∥BC,AB∥CD,
∴△AEG∽△CDG,△CFH∽△ADH,
∴,==,
∴==,S△CDH=2S△CHF,
∴AG=GH=CH,
∴S△ADG=S△DGH=S△CDH,
在△ABG与△CDH中,,
∴△ABG≌△CDH(SAS),
∴S△ABG=S△CDH,
∴S△ADG=S△DGH=S△CDH=S△ABG=2S△CHF,
∴面积是△FHC面积的2倍的所有三角形是△ADG,△DGH,△CDH,△ABG.
25.【解答】解:(1)设A品牌服装每套进价为x元,则B品牌服装每套进价为(x﹣25)元,由题意得:
=×2,
解得:x=100,
经检验:x=100是原分式方程的解,
x﹣25=100﹣25=75,
答:A、B两种品牌服装每套进价分别为100元、75元;
(2)设购进A品牌的服装a套,则购进B品牌服装(2a+4)套,由题意得:
(130﹣100)a+(95﹣75)(2a+4)>1200,
解得:a>16,
答:至少购进A品牌服装的数量是17套.
26.【解答】解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵∠DGF=∠CAB,∠DGF=∠BGE,
∴∠BGE=∠CAB,
∴∠BGE+∠CBA=90°,
∴∠GEB=90°,
∴DE⊥AB;
(2)如图2,连接OD交BC于H,连接BD,
∵AD平分∠CAB,
∴,
∴OD⊥BC,BH=CH,
∵DE⊥AB,OD=OB,
∴S△OBD=OD×BH=OB×DE,
∴BH=DE,
∴BC=2DE.
(3)如图3,作FR⊥AB于R,OS⊥AD于S,
∵AD平分∠CAB,
∴∠CAD=∠BAD=x,
∴∠FBO=90°﹣2x,
∵∠AFO=45°,
∴∠FOB=45°+x,
∴∠OFB=180°﹣(90°﹣2x)﹣(45°+x)=45°+x,
∴∠FOB=∠OFB
∴BF=BO=OA,
∵∠FRB=∠ACB=90°,∠FBR=∠ABC,
∴△BFR∽△BAC,
∴,
∵AC=,
∴FR=,
∴CF=FR=,
∴AF=,tan∠FAR=tan∠FAC=,
设SO=t,AS=2t,SF=SO=t,
则AF=AS+SF=3t=,t=,
∴OF=t=.
27.【解答】解:(1)设A(a,0)(a<0)
∴OB=2OA=﹣2a,即B(0,﹣2a)
∵直线y=kx+2k过点A、B
∴ 解得:
∴直线AB的解析式为:y=2x+4
(2)过点E作EH⊥x轴于点H,
由(1)可得A(﹣2,0)
∵E在线段AB上,xE=t
∴﹣2<t<0,OH=﹣t,EH=yE=2t+4
∵在Rt△CEH中,tan∠DCO=
∴CH=3EH=6t+12
∴CO=CH+HO=6t+12﹣t=5t+12
CA=CO﹣AO=5t+12﹣2=5t+10
∴S=AC?EH=(5t+10)(2t+4)=5t2+20t+20
(3)过G作GM⊥y轴于点M,过E作EN⊥GM于点N,过E作EP∥x轴
∴∠PEC=∠DCO,∠PEN=90°
∵EG⊥CD
∴∠CEG=90°,即∠CEG=∠PEN
∴∠CEG﹣∠PEG=∠PEN﹣∠PEG
即∠PEC=∠GEN=∠DCO
∴tan∠DCO=tan∠GEN=
∵S=5时,5t2+20t+20=5,解得:t1=﹣1,t2=﹣3(舍去)
∴E(﹣1,2),CO=5t+12=7
∴C(﹣7,0)
∵CF∥AB,设直线CF解析式为y=2x+b
2×(﹣7)+b=0 解得:b=14
∴直线CF解析式为y=2x+14
设G(m,2m+14)(﹣7<m<0)
∴GN=﹣1﹣m,NE=2m+14﹣2=2m+12
∴
解得:m=﹣3
∴G(﹣3,8)
同课章节目录
