2018-2019学年湖北省十堰二中七年级(下)期初数学试卷含答案
文档属性
| 名称 | 2018-2019学年湖北省十堰二中七年级(下)期初数学试卷含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 99.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-29 00:00:00 | ||
图片预览




文档简介
2018-2019学年湖北省十堰二中七年级(下)期初数学试卷
一、选择题:(本大题共10个小题,每小题2分,共20分)
1.(2分)如图,直线a、b相交于点O,若∠1等于40°,则∠2等于( )
A.50° B.60° C.140° D.160°
2.(2分)如图,已知AB∥CD,∠A=70°,则∠1度数是( )
A.70° B.100° C.110° D.130°
3.(2分)已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余 C.互补 D.互为对顶角
4.(2分)若m>﹣1,则下列各式中错误的是( )
A.6m>﹣6 B.﹣5m<﹣5 C.m+1>0 D.1﹣m<2
5.(2分)下列各式中,正确的是( )
A.=±4 B.±=4 C.=﹣3 D.=﹣4
6.(2分)为保护生态环境,陕西省某县响应国家“退耕还林”号召,将某一部分耕地改为林地,改变后,林地面积和耕地面积共有180平方千米,耕地面积是林地面积的25%,为求改变后林地面积和耕地面积各多少平方千米.设改变后耕地面积x平方千米,林地地面积y平方千米,根据题意,列出如下四个方程组,其中正确的是( )
A. B.
C. D.
7.(2分)不等式组的解集是( )
A.x<﹣3 B.x<﹣2 C.﹣3<x<﹣2 D.无解
8.(2分)若不等式组的解集为﹣1≤x≤3,则图中表示正确的是( )
A. B.
C. D.
9.(2分)在平面直角坐标系中,点(﹣1,m2+1)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.(2分)如图a∥b,M、N分别在a、b上,P为两平行线间一点,那么∠1+∠2+∠3=( )
A.180° B.270° C.360° D.540°
二、填空题:本大题共8个小题,每小题3分,共24分,把答案直接填在答题卷的横线上.
11.(3分)如图,直线a∥b,直线c与a,b相交.若∠1=70°,则∠2= 度.
12.(3分)如图,已知∠1=70°,∠2=70°,∠3=60°,则∠4= 度.
13.(3分)如图,已知AB∥CD,BE平分∠ABC,∠CDE=150°,则∠C= °.
14.(3分)49的平方根是 ,算术平方根是 ,
15.(3分)不等式5x﹣9≤3(x+1)的解集是 .
16.(3分)如果点P(a,2)在第二象限,那么点Q(﹣3,a)在 .
17.(3分)不等式组的整数解是 .
18.(3分)五女峰森林公园门票价格:成人票每张50元,学生票每张25元.某旅游团买30张门票花了1250元.设其中有x张成人票,y张学生票,根据题意列方程组是 .
三、解答题:
19.(12分)解方程组和不等式(组):
(1)
(2)解不等式2x﹣1<4x+13,并将解集在数轴上表示出来:
(3)
(4)+﹣.
20.(8分)如图,描出A(﹣3,﹣2)、B(2,﹣2)、C(﹣2,1)、D(3,1)四个点,线段AB、CD有什么关系?顺次连接A、B、C、D四点组成的图形是什么图形?
21.(8分)推理填空:
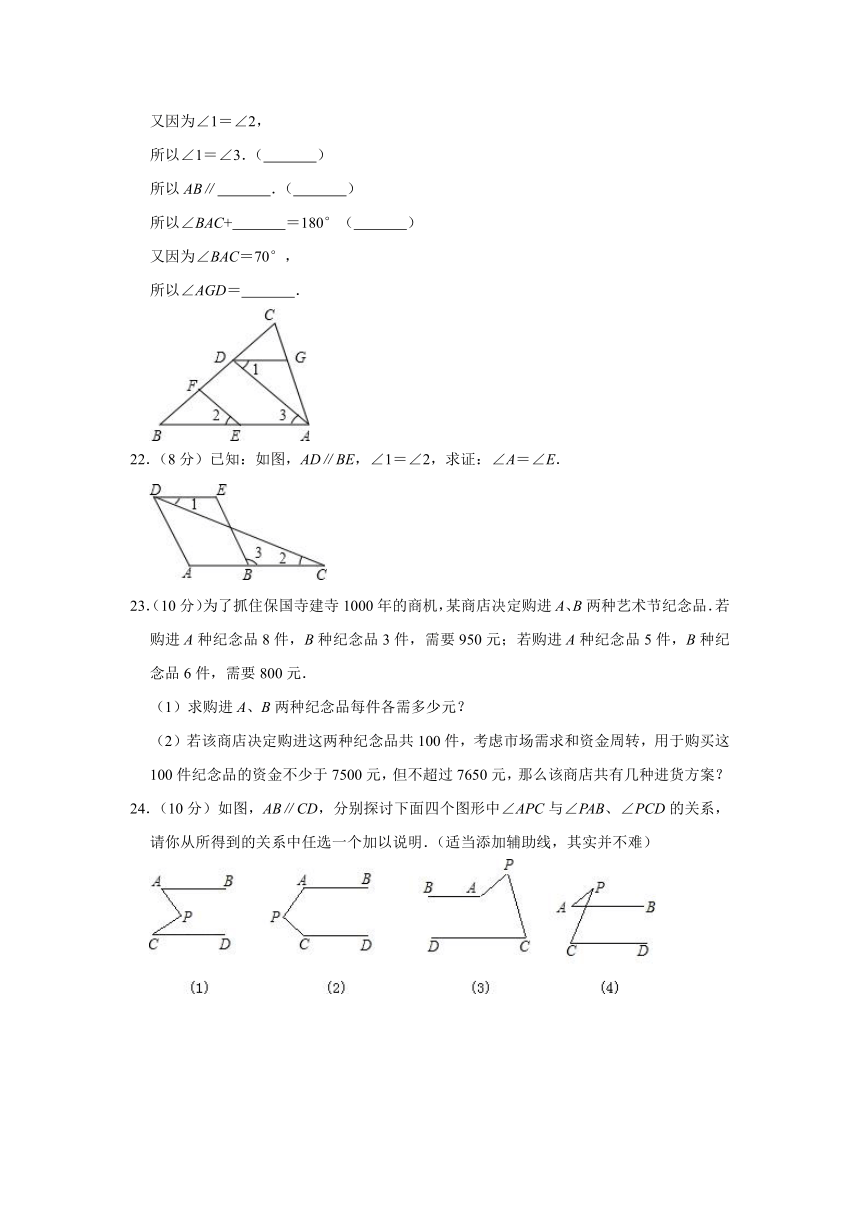
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2= .( )
又因为∠1=∠2,
所以∠1=∠3.( )
所以AB∥ .( )
所以∠BAC+ =180°( )
又因为∠BAC=70°,
所以∠AGD= .
22.(8分)已知:如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
23.(10分)为了抓住保国寺建寺1000年的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
24.(10分)如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明.(适当添加辅助线,其实并不难)
2018-2019学年湖北省十堰二中七年级(下)期初数学试卷
参考答案与试题解析
一、选择题:(本大题共10个小题,每小题2分,共20分)
1.【解答】解:∵∠1+∠2=180°
又∠1=40°
∴∠2=140°.
故选:C.
2.【解答】解:∵AB∥CD,∠A=70°,
∴∠2=70°(两直线平行,内错角相等),
再根据平角的定义,得
∠1=180°﹣70°=110°,
故选:C.
3.【解答】解:图中,∠2=∠COE(对顶角相等),
又∵AB⊥CD,
∴∠1+∠COE=90°,
∴∠1+∠2=90°,
∴两角互余.
故选:B.
4.【解答】解:根据不等式的基本性质可知,
A、6m>﹣6,正确;
B、根据性质3可知,m>﹣1两边同乘以﹣5时,不等式为﹣5m<5,故B错误;
C、m+1>0,正确;
D、1﹣m<2,正确.
故选:B.
5.【解答】解:A、原式=4,所以A选项错误;
B、原式=±4,所以B选项错误;
C、原式=﹣3=,所以C选项正确;
D、原式=|﹣4|=4,所以D选项错误.
故选:C.
6.【解答】解:设耕地面积x平方千米,林地面积为y平方千米,
根据题意列方程组.
故选:B.
7.【解答】解:∵x<﹣2,
由﹣x>3得
x<﹣3,
∴不等式组的解集为:x<﹣3,
故选:A.
8.【解答】解:不等式组的解集为﹣1≤x≤3在数轴表示﹣1和3以及两者之间的部分:
故选:D.
9.【解答】解:因为点(﹣1,m2+1),横坐标<0,纵坐标m2+1一定大于0,
所以满足点在第二象限的条件.
故选:B.
10.【解答】解:过点P作PA∥a,则a∥b∥PA,
∴∠1+∠MPA=180°,∠3+∠NPA=180°,
∴∠1+∠2+∠3=360°.
故选:C.
二、填空题:本大题共8个小题,每小题3分,共24分,把答案直接填在答题卷的横线上.
11.【解答】解:由题意得:直线a∥b,则∠2=∠1=70°
12.【解答】解:∵∠1=70°,∠2=70°,
∴a∥b,
又∵∠3=60°,
∴∠4=∠3=60°
13.【解答】解:∵∠CDE=150°,
∴∠CDB=180﹣∠CDE=30°,
又∵AB∥CD,
∴∠ABD=∠CDB=30°;
∵BE平分∠ABC,
∴∠ABC=60°,
∴∠C=180°﹣60°=120°.
故答案为:120.
14.【解答】解:∵(±7)2=4
∴49的平方根是±7;
又∵=4
∴的算术平方根就是4的算术平方根:=2
故答案为±7,2.
15.【解答】解:不等式去括号,得
5x﹣9≤3x+3,
移项合并同类项,得
2x≤12,
系数化1,得
x≤6.
所以,不等式5x﹣9≤3(x+1)的解集是x≤6.
16.【解答】解:∵点P(a,2)在第二象限,
∴a<0,
∴点Q的横、纵坐标都为负数,
∴点Q在第三象限.
故答案为第三象限.
17.【解答】解:解不等式x﹣2≤0得:x≤2,
解不等式2x﹣1>0得:x>,
即不等式组的解集为:,
符合不等式组解集的整数解为:1,2,
故答案为1,2.
18.【解答】解:设其中有x张成人票,y张儿童票,
根据题意得:.
故答案为:.
三、解答题:
19.【解答】解方程组和不等式和不等式组及实数计算.
解:(1),
由①得x=3+y③,
③代入②得3(3+y)﹣8y=14,
解得y=﹣1,
y=﹣1代入③得,x=2,
方程组的解为;
(2)2x﹣1<4x+13,
移项得2x﹣4x<13+1,
合并同类项得﹣2x<14,
系数化为1得x>﹣7.
在数轴上表示为:
(3),
由①得x<﹣,
由②得x≤15,
不等式组的解集为x<﹣.
(4)+﹣
=2+0﹣
=.
20.【解答】解:如图,
AB∥CD,且AB=CD=5,因而四边形ABDC是平行四边形.
21.【解答】解:∵EF∥AD,
∴∠2=∠3(两直线平行,同位角相等),
∵∠1=∠2,
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠DGA=180°(两直线平行,同旁内角互补),
∵∠BAC=70°,
∴∠AGD=110°,
故答案为:∠3,两直线平行,同位角相等,等量代换,DG,内错角相等,两直线平行,∠AGD,两直线平行,同旁内角互补,110°.
22.【解答】证明:∵AD∥BE,
∴∠A=∠3,
∵∠1=∠2,
∴DE∥AC,
∴∠E=∠3,
∴∠A=∠EBC=∠E.
23.【解答】解:(1)设该商店购进一件A种纪念品需要a元,购进一件B种纪念品需要b元,
根据题意得方程组得:,
解方程组得:,
∴购进一件A种纪念品需要100元,购进一件B种纪念品需要50元;
(2)设该商店购进A种纪念品x个,则购进B种纪念品有(100﹣x)个,
∴,
解得:50≤x≤53,
∵x 为正整数,x=50,51,52,53
∴共有4种进货方案,
分别为:方案1:商店购进A种纪念品50个,则购进B种纪念品有50个;
方案2:商店购进A种纪念品51个,则购进B种纪念品有49个;
方案3:商店购进A种纪念品52个,则购进B种纪念品有48个;
方案4:商店购进A种纪念品53个,则购进B种纪念品有47个.
24.【解答】解:如图:
(1)∠APC=∠PAB+∠PCD;
证明:过点P作PF∥AB,则AB∥CD∥PF,
∴∠APC=∠PAB+∠PCD(两直线平行,内错角相等).
(2)∠APC+∠PAB+∠PCD=360°;
(3)∠APC=∠PAB﹣∠PCD;
(4)∵AB∥CD,
∴∠POB=∠PCD,
∵∠POB是△AOP的外角,
∴∠APC+∠PAB=∠POB,
∴∠APC=∠POB﹣∠PAB,
∴∠APC=∠PCD﹣∠PAB.
一、选择题:(本大题共10个小题,每小题2分,共20分)
1.(2分)如图,直线a、b相交于点O,若∠1等于40°,则∠2等于( )
A.50° B.60° C.140° D.160°
2.(2分)如图,已知AB∥CD,∠A=70°,则∠1度数是( )
A.70° B.100° C.110° D.130°
3.(2分)已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余 C.互补 D.互为对顶角
4.(2分)若m>﹣1,则下列各式中错误的是( )
A.6m>﹣6 B.﹣5m<﹣5 C.m+1>0 D.1﹣m<2
5.(2分)下列各式中,正确的是( )
A.=±4 B.±=4 C.=﹣3 D.=﹣4
6.(2分)为保护生态环境,陕西省某县响应国家“退耕还林”号召,将某一部分耕地改为林地,改变后,林地面积和耕地面积共有180平方千米,耕地面积是林地面积的25%,为求改变后林地面积和耕地面积各多少平方千米.设改变后耕地面积x平方千米,林地地面积y平方千米,根据题意,列出如下四个方程组,其中正确的是( )
A. B.
C. D.
7.(2分)不等式组的解集是( )
A.x<﹣3 B.x<﹣2 C.﹣3<x<﹣2 D.无解
8.(2分)若不等式组的解集为﹣1≤x≤3,则图中表示正确的是( )
A. B.
C. D.
9.(2分)在平面直角坐标系中,点(﹣1,m2+1)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.(2分)如图a∥b,M、N分别在a、b上,P为两平行线间一点,那么∠1+∠2+∠3=( )
A.180° B.270° C.360° D.540°
二、填空题:本大题共8个小题,每小题3分,共24分,把答案直接填在答题卷的横线上.
11.(3分)如图,直线a∥b,直线c与a,b相交.若∠1=70°,则∠2= 度.
12.(3分)如图,已知∠1=70°,∠2=70°,∠3=60°,则∠4= 度.
13.(3分)如图,已知AB∥CD,BE平分∠ABC,∠CDE=150°,则∠C= °.
14.(3分)49的平方根是 ,算术平方根是 ,
15.(3分)不等式5x﹣9≤3(x+1)的解集是 .
16.(3分)如果点P(a,2)在第二象限,那么点Q(﹣3,a)在 .
17.(3分)不等式组的整数解是 .
18.(3分)五女峰森林公园门票价格:成人票每张50元,学生票每张25元.某旅游团买30张门票花了1250元.设其中有x张成人票,y张学生票,根据题意列方程组是 .
三、解答题:
19.(12分)解方程组和不等式(组):
(1)
(2)解不等式2x﹣1<4x+13,并将解集在数轴上表示出来:
(3)
(4)+﹣.
20.(8分)如图,描出A(﹣3,﹣2)、B(2,﹣2)、C(﹣2,1)、D(3,1)四个点,线段AB、CD有什么关系?顺次连接A、B、C、D四点组成的图形是什么图形?
21.(8分)推理填空:
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2= .( )
又因为∠1=∠2,
所以∠1=∠3.( )
所以AB∥ .( )
所以∠BAC+ =180°( )
又因为∠BAC=70°,
所以∠AGD= .
22.(8分)已知:如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
23.(10分)为了抓住保国寺建寺1000年的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
24.(10分)如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明.(适当添加辅助线,其实并不难)
2018-2019学年湖北省十堰二中七年级(下)期初数学试卷
参考答案与试题解析
一、选择题:(本大题共10个小题,每小题2分,共20分)
1.【解答】解:∵∠1+∠2=180°
又∠1=40°
∴∠2=140°.
故选:C.
2.【解答】解:∵AB∥CD,∠A=70°,
∴∠2=70°(两直线平行,内错角相等),
再根据平角的定义,得
∠1=180°﹣70°=110°,
故选:C.
3.【解答】解:图中,∠2=∠COE(对顶角相等),
又∵AB⊥CD,
∴∠1+∠COE=90°,
∴∠1+∠2=90°,
∴两角互余.
故选:B.
4.【解答】解:根据不等式的基本性质可知,
A、6m>﹣6,正确;
B、根据性质3可知,m>﹣1两边同乘以﹣5时,不等式为﹣5m<5,故B错误;
C、m+1>0,正确;
D、1﹣m<2,正确.
故选:B.
5.【解答】解:A、原式=4,所以A选项错误;
B、原式=±4,所以B选项错误;
C、原式=﹣3=,所以C选项正确;
D、原式=|﹣4|=4,所以D选项错误.
故选:C.
6.【解答】解:设耕地面积x平方千米,林地面积为y平方千米,
根据题意列方程组.
故选:B.
7.【解答】解:∵x<﹣2,
由﹣x>3得
x<﹣3,
∴不等式组的解集为:x<﹣3,
故选:A.
8.【解答】解:不等式组的解集为﹣1≤x≤3在数轴表示﹣1和3以及两者之间的部分:
故选:D.
9.【解答】解:因为点(﹣1,m2+1),横坐标<0,纵坐标m2+1一定大于0,
所以满足点在第二象限的条件.
故选:B.
10.【解答】解:过点P作PA∥a,则a∥b∥PA,
∴∠1+∠MPA=180°,∠3+∠NPA=180°,
∴∠1+∠2+∠3=360°.
故选:C.
二、填空题:本大题共8个小题,每小题3分,共24分,把答案直接填在答题卷的横线上.
11.【解答】解:由题意得:直线a∥b,则∠2=∠1=70°
12.【解答】解:∵∠1=70°,∠2=70°,
∴a∥b,
又∵∠3=60°,
∴∠4=∠3=60°
13.【解答】解:∵∠CDE=150°,
∴∠CDB=180﹣∠CDE=30°,
又∵AB∥CD,
∴∠ABD=∠CDB=30°;
∵BE平分∠ABC,
∴∠ABC=60°,
∴∠C=180°﹣60°=120°.
故答案为:120.
14.【解答】解:∵(±7)2=4
∴49的平方根是±7;
又∵=4
∴的算术平方根就是4的算术平方根:=2
故答案为±7,2.
15.【解答】解:不等式去括号,得
5x﹣9≤3x+3,
移项合并同类项,得
2x≤12,
系数化1,得
x≤6.
所以,不等式5x﹣9≤3(x+1)的解集是x≤6.
16.【解答】解:∵点P(a,2)在第二象限,
∴a<0,
∴点Q的横、纵坐标都为负数,
∴点Q在第三象限.
故答案为第三象限.
17.【解答】解:解不等式x﹣2≤0得:x≤2,
解不等式2x﹣1>0得:x>,
即不等式组的解集为:,
符合不等式组解集的整数解为:1,2,
故答案为1,2.
18.【解答】解:设其中有x张成人票,y张儿童票,
根据题意得:.
故答案为:.
三、解答题:
19.【解答】解方程组和不等式和不等式组及实数计算.
解:(1),
由①得x=3+y③,
③代入②得3(3+y)﹣8y=14,
解得y=﹣1,
y=﹣1代入③得,x=2,
方程组的解为;
(2)2x﹣1<4x+13,
移项得2x﹣4x<13+1,
合并同类项得﹣2x<14,
系数化为1得x>﹣7.
在数轴上表示为:
(3),
由①得x<﹣,
由②得x≤15,
不等式组的解集为x<﹣.
(4)+﹣
=2+0﹣
=.
20.【解答】解:如图,
AB∥CD,且AB=CD=5,因而四边形ABDC是平行四边形.
21.【解答】解:∵EF∥AD,
∴∠2=∠3(两直线平行,同位角相等),
∵∠1=∠2,
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠DGA=180°(两直线平行,同旁内角互补),
∵∠BAC=70°,
∴∠AGD=110°,
故答案为:∠3,两直线平行,同位角相等,等量代换,DG,内错角相等,两直线平行,∠AGD,两直线平行,同旁内角互补,110°.
22.【解答】证明:∵AD∥BE,
∴∠A=∠3,
∵∠1=∠2,
∴DE∥AC,
∴∠E=∠3,
∴∠A=∠EBC=∠E.
23.【解答】解:(1)设该商店购进一件A种纪念品需要a元,购进一件B种纪念品需要b元,
根据题意得方程组得:,
解方程组得:,
∴购进一件A种纪念品需要100元,购进一件B种纪念品需要50元;
(2)设该商店购进A种纪念品x个,则购进B种纪念品有(100﹣x)个,
∴,
解得:50≤x≤53,
∵x 为正整数,x=50,51,52,53
∴共有4种进货方案,
分别为:方案1:商店购进A种纪念品50个,则购进B种纪念品有50个;
方案2:商店购进A种纪念品51个,则购进B种纪念品有49个;
方案3:商店购进A种纪念品52个,则购进B种纪念品有48个;
方案4:商店购进A种纪念品53个,则购进B种纪念品有47个.
24.【解答】解:如图:
(1)∠APC=∠PAB+∠PCD;
证明:过点P作PF∥AB,则AB∥CD∥PF,
∴∠APC=∠PAB+∠PCD(两直线平行,内错角相等).
(2)∠APC+∠PAB+∠PCD=360°;
(3)∠APC=∠PAB﹣∠PCD;
(4)∵AB∥CD,
∴∠POB=∠PCD,
∵∠POB是△AOP的外角,
∴∠APC+∠PAB=∠POB,
∴∠APC=∠POB﹣∠PAB,
∴∠APC=∠PCD﹣∠PAB.
同课章节目录
