2020版高中数学新人教B版选修1-1第二章圆锥曲线与方程2.2.1双曲线及其标准方程课件(36张)
文档属性
| 名称 | 2020版高中数学新人教B版选修1-1第二章圆锥曲线与方程2.2.1双曲线及其标准方程课件(36张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-29 00:00:00 | ||
图片预览











文档简介
课件36张PPT。2.2.1 双曲线及其标准方程第二章 §2.2 双曲线学习目标XUEXIMUBIAO1.了解双曲线的定义、几何图形和标准方程的推导过程.
2.掌握双曲线的标准方程及其求法.
3.会利用双曲线的定义和标准方程解决简单的问题.NEIRONGSUOYIN内容索引自主学习题型探究达标检测1自主学习PART ONE知识点一 双曲线的定义
平面内到两个定点F1,F2的距离的 等于定值2a(大于0且小于|F1F2|)的点的轨迹叫做双曲线,这两个定点叫做 ,_______
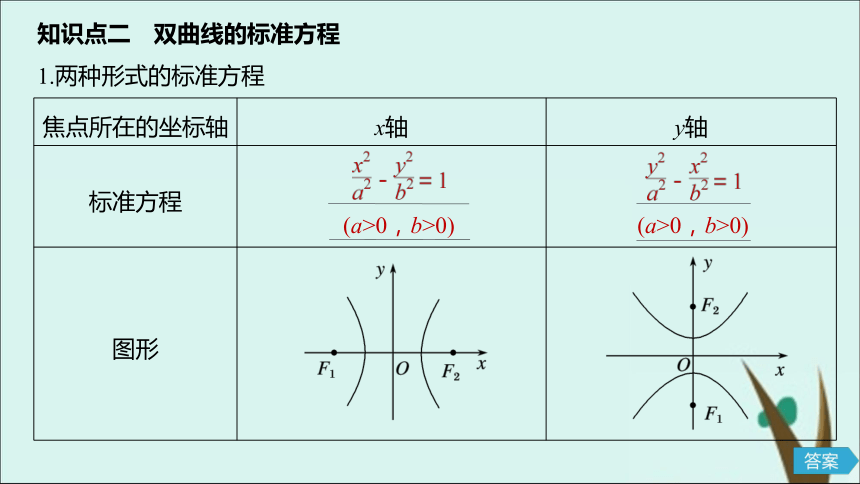
叫做双曲线的焦距.差的绝对值双曲线的焦点两焦点间的距离知识点二 双曲线的标准方程
1.两种形式的标准方程(a>0,b>0)(a>0,b>0)F1(-c,0),F2(c,0)F1(0,-c),F2(0,c)a2+b2=c22.焦点F1,F2的位置是双曲线定位的条件,它决定了双曲线标准方程的类型.“焦点跟着正项走”,若x2项的系数为正,则焦点在 上;若y2项的系数为正,那么焦点在 上.
3.当双曲线的焦点位置不确定时,可设其标准方程为Ax2+By2=1(AB<0).
4.标准方程中的两个参数a和b,确定了双曲线的形状和大小,是双曲线的定形条件,这里的b2= 要与椭圆中的b2= 相区别.x轴y轴c2-a2a2-c21.平面内到两定点的距离的差等于常数(小于两定点间距离)的点的轨迹是双曲线.( )
2.在双曲线标准方程 中,a>0,b>0且a≠b.( )
3.在双曲线标准方程中,a,b的大小关系是a>b.( )思考辨析 判断正误SIKAOBIANXIPANDUANZHENGWU×××2题型探究PART TWO题型一 求双曲线的标准方程例1 求下列双曲线的标准方程.解得λ=20或λ=7(舍去),(2)焦距为26,且经过点M(0,12);解 因为双曲线经过点M(0,12),所以M(0,12)为双曲线的一个顶点,故焦点在y轴上,且a=12.
又2c=26,所以c=13,所以b2=c2-a2=25.解 设双曲线方程为mx2+ny2=1(mn<0).反思感悟 待定系数法求方程的步骤
(1)定型:即确定双曲线的焦点所在的坐标轴是x轴还是y轴.
(2)设方程:根据焦点位置设出相应的标准方程的形式,
①若不知道焦点的位置,则进行讨论,或设双曲线的方程为Ax2+By2=1(AB<0).(3)计算:利用题中条件列出方程组,求出相关值.
(4)结论:写出双曲线的标准方程.跟踪训练1 根据条件求双曲线的标准方程.解得a2=5或a2=30(舍).解 设双曲线方程为mx2+ny2=1(mn<0).题型二 双曲线的定义及应用例2 (1)如图,已知双曲线的方程为 (a>0,b>0),点A,B均在双曲线的右支上,线段AB经过双曲线的右焦点F2,|AB|=m,F1为双曲线的左焦点,则△ABF1的周长为________.4a+2m解析 由双曲线的定义,知|AF1|-|AF2|=2a,
|BF1|-|BF2|=2a.
又|AF2|+|BF2|=|AB|,
所以△ABF1的周长为|AF1|+|BF1|+|AB|
=4a+2|AB|=4a+2m.(2)已知双曲线 的左、右焦点分别是F1,F2,若双曲线上一点P使得∠F1PF2=60°,则△F1PF2的面积为_____.由双曲线定义和余弦定理,得|PF1|-|PF2|=±6,
|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos 60°,
所以102=(|PF1|-|PF2|)2+|PF1|·|PF2|,
所以|PF1|·|PF2|=64,引申探究
本例(2)中若∠F1PF2=90°,其他条件不变,求△F1PF2的面积.解 由双曲线方程知a=3,b=4,c=5,
由双曲线的定义得||PF1|-|PF2||=2a=6,
所以|PF1|2+|PF2|2-2|PF1|·|PF2|=36. ①
在Rt△F1PF2中,由勾股定理得|PF1|2+|PF2|2=|F1F2|2=(2c)2=100. ②
将②代入①得|PF1|·|PF2|=32,反思感悟 求双曲线中焦点三角形面积的方法
(1)方法一:
①根据双曲线的定义求出||PF1|-|PF2||=2a;
②利用余弦定理表示出|PF1|,|PF2|,|F1F2|之间满足的关系式;
③通过配方,利用整体的思想求出|PF1|·|PF2|的值;④利用公式 = ×|PF1|·|PF2|sin∠F1PF2求得面积.
(2)方法二:利用公式 = ×|F1F2|×|yP|(yP为P点的纵坐标)求得面积.特别提醒:利用双曲线的定义解决与焦点有关的问题,一是要注意定义条件||PF1|-|PF2||=2a的变形使用,特别是与|PF1|2+|PF2|2,|PF1|·|PF2|间的关系.跟踪训练2 已知双曲线的方程是 ,点P在双曲线上,且到其中一个焦点F1的距离为10,点N是PF1的中点,求|ON|的大小(O为坐标原点).因为||PF1|-|PF2||=2a=8,|PF1|=10,典例 已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,则动圆圆心M的轨迹方程为________________.核心素养之直观想象HEXINSUYANGZHIZHIGUANXIANGXIANG由双曲线的定义求轨迹方程解析 如图,设动圆M与圆C1及圆C2分别外切于点A和B,根据两圆外切的条件 |MC1|-|AC1|=|MA|,|MC2|-|BC2|=|MB|,
因为|MA|=|MB|,
所以|MC1|-|AC1|=|MC2|-|BC2|,
即|MC2|-|MC1|=2,这表明动点M与两定点C2,C1
的距离的差是常数2且2<6=|C1C2|.
根据双曲线的定义,动点M的轨迹为双曲线的左支(点M与C2的距离大,与C1的距离小),这里a=1,c=3,素养评析 (1)定义法求双曲线方程的注意点
①注意条件中是到定点距离之差,还是差的绝对值.
②当差的绝对值为常数时要注意常数与两定点间距离的大小问题.
③求出方程后要注意表示满足方程的解的坐标是否都在所给的曲线上.
(2)建立数与形的联系,探索解决数学问题的思路,提升数形结合能力,形成数学直观直觉,有利于培养学生的数学思维品质和关键能力.3达标检测PART THREE1.到两定点F1(-3,0),F2(3,0)的距离之差的绝对值等于6的点M的轨迹是
A.椭圆 B.线段
C.双曲线 D.两条射线√12345解析 由题意知|F1F2|=||MF1|-|MF2||=6,
所以点M的轨迹是两条射线.解析 由题意知,k+3>0且k+2<0,
∴-3C.k<-3或k>-2 D.k>-2√12345又由|F1F2|=10,可得△PF1F2是直角三角形,√12345√解析 由于a>0,0<a2<4,且4-a2=a+2,所以可解得a=1,故选D.123455.求适合下列条件的双曲线的标准方程.
(1)a=3,c=4,焦点在x轴上;解 由题设知,a=3,c=4,
由c2=a2+b2,得b2=c2-a2=42-32=7.
因为双曲线的焦点在x轴上,12345(2)焦点为(0,-6),(0,6),经过点A(-5,6).解 由已知得c=6,且焦点在y轴上,
因为点A(-5,6)在双曲线上,则a=4,b2=c2-a2=62-42=20.课堂小结KETANGXIAOJIE1.双曲线定义中||PF1|-|PF2||=2a(2a<|F1F2|)不要漏了绝对值符号,当2a=|F1F2|时表示两条射线.
2.在双曲线的标准方程中,a>b不一定成立,要注意与椭圆中a,b,c的区别.在椭圆中a2=b2+c2,在双曲线中c2=a2+b2.
3.用待定系数法求双曲线的标准方程时,要先判断焦点所在的位置,设出标准方程后,由条件列出a,b,c的方程组.
如果焦点不确定要分类讨论,采用待定系数法求方程或用形如mx2+ny2=1(mn<0)的形式求解.
2.掌握双曲线的标准方程及其求法.
3.会利用双曲线的定义和标准方程解决简单的问题.NEIRONGSUOYIN内容索引自主学习题型探究达标检测1自主学习PART ONE知识点一 双曲线的定义
平面内到两个定点F1,F2的距离的 等于定值2a(大于0且小于|F1F2|)的点的轨迹叫做双曲线,这两个定点叫做 ,_______
叫做双曲线的焦距.差的绝对值双曲线的焦点两焦点间的距离知识点二 双曲线的标准方程
1.两种形式的标准方程(a>0,b>0)(a>0,b>0)F1(-c,0),F2(c,0)F1(0,-c),F2(0,c)a2+b2=c22.焦点F1,F2的位置是双曲线定位的条件,它决定了双曲线标准方程的类型.“焦点跟着正项走”,若x2项的系数为正,则焦点在 上;若y2项的系数为正,那么焦点在 上.
3.当双曲线的焦点位置不确定时,可设其标准方程为Ax2+By2=1(AB<0).
4.标准方程中的两个参数a和b,确定了双曲线的形状和大小,是双曲线的定形条件,这里的b2= 要与椭圆中的b2= 相区别.x轴y轴c2-a2a2-c21.平面内到两定点的距离的差等于常数(小于两定点间距离)的点的轨迹是双曲线.( )
2.在双曲线标准方程 中,a>0,b>0且a≠b.( )
3.在双曲线标准方程中,a,b的大小关系是a>b.( )思考辨析 判断正误SIKAOBIANXIPANDUANZHENGWU×××2题型探究PART TWO题型一 求双曲线的标准方程例1 求下列双曲线的标准方程.解得λ=20或λ=7(舍去),(2)焦距为26,且经过点M(0,12);解 因为双曲线经过点M(0,12),所以M(0,12)为双曲线的一个顶点,故焦点在y轴上,且a=12.
又2c=26,所以c=13,所以b2=c2-a2=25.解 设双曲线方程为mx2+ny2=1(mn<0).反思感悟 待定系数法求方程的步骤
(1)定型:即确定双曲线的焦点所在的坐标轴是x轴还是y轴.
(2)设方程:根据焦点位置设出相应的标准方程的形式,
①若不知道焦点的位置,则进行讨论,或设双曲线的方程为Ax2+By2=1(AB<0).(3)计算:利用题中条件列出方程组,求出相关值.
(4)结论:写出双曲线的标准方程.跟踪训练1 根据条件求双曲线的标准方程.解得a2=5或a2=30(舍).解 设双曲线方程为mx2+ny2=1(mn<0).题型二 双曲线的定义及应用例2 (1)如图,已知双曲线的方程为 (a>0,b>0),点A,B均在双曲线的右支上,线段AB经过双曲线的右焦点F2,|AB|=m,F1为双曲线的左焦点,则△ABF1的周长为________.4a+2m解析 由双曲线的定义,知|AF1|-|AF2|=2a,
|BF1|-|BF2|=2a.
又|AF2|+|BF2|=|AB|,
所以△ABF1的周长为|AF1|+|BF1|+|AB|
=4a+2|AB|=4a+2m.(2)已知双曲线 的左、右焦点分别是F1,F2,若双曲线上一点P使得∠F1PF2=60°,则△F1PF2的面积为_____.由双曲线定义和余弦定理,得|PF1|-|PF2|=±6,
|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos 60°,
所以102=(|PF1|-|PF2|)2+|PF1|·|PF2|,
所以|PF1|·|PF2|=64,引申探究
本例(2)中若∠F1PF2=90°,其他条件不变,求△F1PF2的面积.解 由双曲线方程知a=3,b=4,c=5,
由双曲线的定义得||PF1|-|PF2||=2a=6,
所以|PF1|2+|PF2|2-2|PF1|·|PF2|=36. ①
在Rt△F1PF2中,由勾股定理得|PF1|2+|PF2|2=|F1F2|2=(2c)2=100. ②
将②代入①得|PF1|·|PF2|=32,反思感悟 求双曲线中焦点三角形面积的方法
(1)方法一:
①根据双曲线的定义求出||PF1|-|PF2||=2a;
②利用余弦定理表示出|PF1|,|PF2|,|F1F2|之间满足的关系式;
③通过配方,利用整体的思想求出|PF1|·|PF2|的值;④利用公式 = ×|PF1|·|PF2|sin∠F1PF2求得面积.
(2)方法二:利用公式 = ×|F1F2|×|yP|(yP为P点的纵坐标)求得面积.特别提醒:利用双曲线的定义解决与焦点有关的问题,一是要注意定义条件||PF1|-|PF2||=2a的变形使用,特别是与|PF1|2+|PF2|2,|PF1|·|PF2|间的关系.跟踪训练2 已知双曲线的方程是 ,点P在双曲线上,且到其中一个焦点F1的距离为10,点N是PF1的中点,求|ON|的大小(O为坐标原点).因为||PF1|-|PF2||=2a=8,|PF1|=10,典例 已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,则动圆圆心M的轨迹方程为________________.核心素养之直观想象HEXINSUYANGZHIZHIGUANXIANGXIANG由双曲线的定义求轨迹方程解析 如图,设动圆M与圆C1及圆C2分别外切于点A和B,根据两圆外切的条件 |MC1|-|AC1|=|MA|,|MC2|-|BC2|=|MB|,
因为|MA|=|MB|,
所以|MC1|-|AC1|=|MC2|-|BC2|,
即|MC2|-|MC1|=2,这表明动点M与两定点C2,C1
的距离的差是常数2且2<6=|C1C2|.
根据双曲线的定义,动点M的轨迹为双曲线的左支(点M与C2的距离大,与C1的距离小),这里a=1,c=3,素养评析 (1)定义法求双曲线方程的注意点
①注意条件中是到定点距离之差,还是差的绝对值.
②当差的绝对值为常数时要注意常数与两定点间距离的大小问题.
③求出方程后要注意表示满足方程的解的坐标是否都在所给的曲线上.
(2)建立数与形的联系,探索解决数学问题的思路,提升数形结合能力,形成数学直观直觉,有利于培养学生的数学思维品质和关键能力.3达标检测PART THREE1.到两定点F1(-3,0),F2(3,0)的距离之差的绝对值等于6的点M的轨迹是
A.椭圆 B.线段
C.双曲线 D.两条射线√12345解析 由题意知|F1F2|=||MF1|-|MF2||=6,
所以点M的轨迹是两条射线.解析 由题意知,k+3>0且k+2<0,
∴-3
(1)a=3,c=4,焦点在x轴上;解 由题设知,a=3,c=4,
由c2=a2+b2,得b2=c2-a2=42-32=7.
因为双曲线的焦点在x轴上,12345(2)焦点为(0,-6),(0,6),经过点A(-5,6).解 由已知得c=6,且焦点在y轴上,
因为点A(-5,6)在双曲线上,则a=4,b2=c2-a2=62-42=20.课堂小结KETANGXIAOJIE1.双曲线定义中||PF1|-|PF2||=2a(2a<|F1F2|)不要漏了绝对值符号,当2a=|F1F2|时表示两条射线.
2.在双曲线的标准方程中,a>b不一定成立,要注意与椭圆中a,b,c的区别.在椭圆中a2=b2+c2,在双曲线中c2=a2+b2.
3.用待定系数法求双曲线的标准方程时,要先判断焦点所在的位置,设出标准方程后,由条件列出a,b,c的方程组.
如果焦点不确定要分类讨论,采用待定系数法求方程或用形如mx2+ny2=1(mn<0)的形式求解.
