2020版高中数学新人教B版选修1-1第二章圆锥曲线与方程微专题突破二离心率的求法课件
文档属性
| 名称 | 2020版高中数学新人教B版选修1-1第二章圆锥曲线与方程微专题突破二离心率的求法课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-29 00:00:00 | ||
图片预览











文档简介
课件41张PPT。专题突破二 离心率的求法第二章 圆锥曲线与方程一、以渐近线为指向求离心率
例1 已知双曲线两渐近线的夹角为60°,则双曲线的离心率为________.思维切入 双曲线的两渐近线有两种情况,焦点位置也有两种情况,分别讨论即可.解析 由题意知,双曲线的渐近线存在两种情况.
当双曲线的焦点在x轴上时,若其中一条渐近线的倾斜角为60°,如图1所示;
若其中一条渐近线的倾斜角为30°,如图2所示. 跟踪训练1 中心在原点,焦点在x轴上的双曲线的一条渐近线经过点(4,-2),则它的离心率为√二、以焦点三角形为指向求离心率
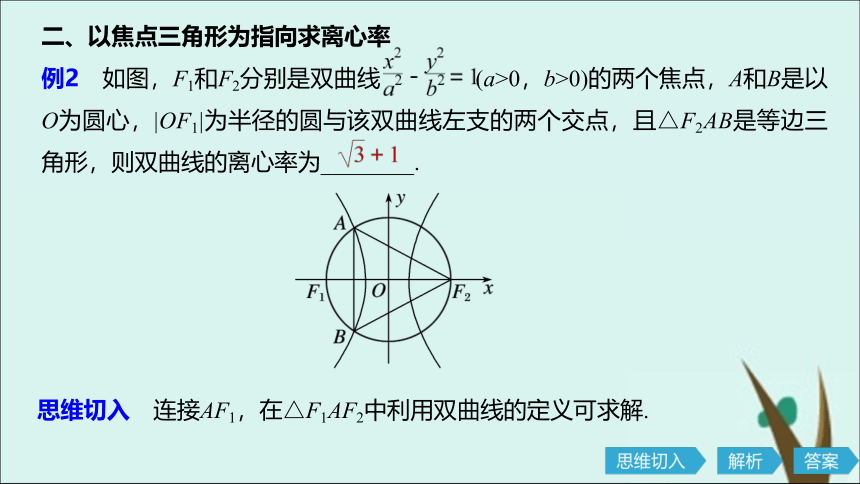
例2 如图,F1和F2分别是双曲线 (a>0,b>0)的两个焦点,A和B是以O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则双曲线的离心率为________.思维切入 连接AF1,在△F1AF2中利用双曲线的定义可求解.解析 方法一 如图,连接AF1,由△F2AB是等边三角形,知∠AF2F1=30°.
易知△AF1F2为直角三角形,方法二 如图,连接AF1,易得∠F1AF2=90°,
β=∠F1F2A=30°,α=∠F2F1A=60°,点评 涉及到焦点三角形的题目往往利用圆锥曲线的定义求得 的值.√解析 方法一 如图,
在Rt△PF2F1中,∠PF1F2=30°,|F1F2|=2c,∵|PF1|+|PF2|=2a,方法二 (特殊值法):
在Rt△PF2F1中,令|PF2|=1,∵∠PF1F2=30°,三、寻求齐次方程求离心率
例3 已知双曲线E: (a>0,b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且2|AB|=3|BC|,则E的离心率是____.思维切入 通过2|AB|=3|BC|,得到a,b,c的关系式,
再由b2=c2-a2,得到a和c的关系式,同时除以a2,即可得到关于e的一元二次方程,求得e.2|BC|=2c.
又2|AB|=3|BC|,即2b2=3ac,
∴2(c2-a2)=3ac,
两边同除以a2并整理得2e2-3e-2=0,
解得e=2(负值舍去).点评 求圆锥曲线的离心率,就是求a和c的值或a和c的关系,然后根据离心率的定义求得.但在多数情况下,由于受到题目已知条件的限制,很难或不可能求出a和c的值,只能将条件整理成关于a和c的关系式,进而求得 的值,其关键是善于利用定义以及图形中的几何关系来建立关于参数a,b,c的关系式,结合c2=a2+b2,化简为参数a,c的关系式进行求解.跟踪训练3 已知椭圆 (a>b>0),A,B分别为椭圆的左顶点和上顶点,F为右焦点,且AB⊥BF,则椭圆的离心率为_______.由AB⊥BF得|AB|2+|BF|2=|AF|2,
将b2=a2-c2代入,得a2-ac-c2=0,四、利用直线与圆锥曲线的位置关系求离心率的取值范围[2,+∞)故离心率e的取值范围是[2,+∞).√由于直线与双曲线相交于两个不同的点,
则1-a2≠0?a2≠1,且此时Δ=4a2(2-a2)>0?a2<2,
所以a2∈(0,1)∪(1,2).五、利用焦半径的性质求离心率的取值范围又因为点P在椭圆上,所以|PF1|+|PF2|=2a.又a-c<|PF2|(1)椭圆焦半径的取值范围为[a-c,a+c].
(2)双曲线的焦半径:
①点P与焦点F位于y轴同侧时,其取值范围为[c-a,+∞);
②点P与焦点F位于y轴异侧时,其取值范围为[c+a,+∞).√解析 ∵P在双曲线的右支上,
∴由双曲线的定义可得|PF1|-|PF2|=2a,
∵|PF1|=4|PF2|,
∴4|PF2|-|PF2|=2a,根据点P在双曲线的右支上,12345√针对训练ZHENDUIXUNLIAN67123456712345√67123453.如图,已知F1,F2分别是椭圆的左、右焦点,现以F2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M,N,若过F1的直线MF1是圆F2的切线,则椭圆的离心率为√6712345解析 ∵过F1的直线MF1是圆F2的切线,
∴∠F1MF2=90°,|MF2|=c,∵|F1F2|=2c,6712345√6712345解析 由题设条件可知△ABF2为等腰三角形,且AF2=BF2,
只要∠AF2B为钝角即可.故选B.675.过双曲线C: (a>0,b>0)的右焦点作一条与其渐近线平行的直线,交C于点P.若点P的横坐标为2a,则C的离心率为________.123456712345676.已知双曲线 (a>0,b>0)的左、右焦点分别为F1,F2,点M在双曲线的左支上,且|MF2|=7|MF1|,则此双曲线的离心率的最大值为____.12345解析 因为|MF2|=7|MF1|,
所以|MF2|-|MF1|=6|MF1|,
即2a=6|MF1|≥6(c-a),故8a≥6c,当且仅当M为双曲线的左顶点时,等号成立.677.已知椭圆C: (a>b>0)的左、右焦点分别为F1,F2,点P在椭圆C上,线段PF2与圆:x2+y2=b2相切于点Q,若Q是线段PF2的中点,e为C的离心率,则 的最小值是________.1234567解析 如图,连接PF1,OQ,由OQ为△PF1F2的中位线,由圆x2+y2=b2,
可得|OQ|=b,则|PF1|=2b.
由椭圆的定义可得|PF1|+|PF2|=2a,
即|PF2|=2a-2b.
又OQ⊥PF2,所以PF1⊥PF2,
即(2b)2+(2a-2b)2=(2c)2,
即b2+a2-2ab+b2=c2=a2-b2,12345671234567
例1 已知双曲线两渐近线的夹角为60°,则双曲线的离心率为________.思维切入 双曲线的两渐近线有两种情况,焦点位置也有两种情况,分别讨论即可.解析 由题意知,双曲线的渐近线存在两种情况.
当双曲线的焦点在x轴上时,若其中一条渐近线的倾斜角为60°,如图1所示;
若其中一条渐近线的倾斜角为30°,如图2所示. 跟踪训练1 中心在原点,焦点在x轴上的双曲线的一条渐近线经过点(4,-2),则它的离心率为√二、以焦点三角形为指向求离心率
例2 如图,F1和F2分别是双曲线 (a>0,b>0)的两个焦点,A和B是以O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则双曲线的离心率为________.思维切入 连接AF1,在△F1AF2中利用双曲线的定义可求解.解析 方法一 如图,连接AF1,由△F2AB是等边三角形,知∠AF2F1=30°.
易知△AF1F2为直角三角形,方法二 如图,连接AF1,易得∠F1AF2=90°,
β=∠F1F2A=30°,α=∠F2F1A=60°,点评 涉及到焦点三角形的题目往往利用圆锥曲线的定义求得 的值.√解析 方法一 如图,
在Rt△PF2F1中,∠PF1F2=30°,|F1F2|=2c,∵|PF1|+|PF2|=2a,方法二 (特殊值法):
在Rt△PF2F1中,令|PF2|=1,∵∠PF1F2=30°,三、寻求齐次方程求离心率
例3 已知双曲线E: (a>0,b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且2|AB|=3|BC|,则E的离心率是____.思维切入 通过2|AB|=3|BC|,得到a,b,c的关系式,
再由b2=c2-a2,得到a和c的关系式,同时除以a2,即可得到关于e的一元二次方程,求得e.2|BC|=2c.
又2|AB|=3|BC|,即2b2=3ac,
∴2(c2-a2)=3ac,
两边同除以a2并整理得2e2-3e-2=0,
解得e=2(负值舍去).点评 求圆锥曲线的离心率,就是求a和c的值或a和c的关系,然后根据离心率的定义求得.但在多数情况下,由于受到题目已知条件的限制,很难或不可能求出a和c的值,只能将条件整理成关于a和c的关系式,进而求得 的值,其关键是善于利用定义以及图形中的几何关系来建立关于参数a,b,c的关系式,结合c2=a2+b2,化简为参数a,c的关系式进行求解.跟踪训练3 已知椭圆 (a>b>0),A,B分别为椭圆的左顶点和上顶点,F为右焦点,且AB⊥BF,则椭圆的离心率为_______.由AB⊥BF得|AB|2+|BF|2=|AF|2,
将b2=a2-c2代入,得a2-ac-c2=0,四、利用直线与圆锥曲线的位置关系求离心率的取值范围[2,+∞)故离心率e的取值范围是[2,+∞).√由于直线与双曲线相交于两个不同的点,
则1-a2≠0?a2≠1,且此时Δ=4a2(2-a2)>0?a2<2,
所以a2∈(0,1)∪(1,2).五、利用焦半径的性质求离心率的取值范围又因为点P在椭圆上,所以|PF1|+|PF2|=2a.又a-c<|PF2|
(2)双曲线的焦半径:
①点P与焦点F位于y轴同侧时,其取值范围为[c-a,+∞);
②点P与焦点F位于y轴异侧时,其取值范围为[c+a,+∞).√解析 ∵P在双曲线的右支上,
∴由双曲线的定义可得|PF1|-|PF2|=2a,
∵|PF1|=4|PF2|,
∴4|PF2|-|PF2|=2a,根据点P在双曲线的右支上,12345√针对训练ZHENDUIXUNLIAN67123456712345√67123453.如图,已知F1,F2分别是椭圆的左、右焦点,现以F2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M,N,若过F1的直线MF1是圆F2的切线,则椭圆的离心率为√6712345解析 ∵过F1的直线MF1是圆F2的切线,
∴∠F1MF2=90°,|MF2|=c,∵|F1F2|=2c,6712345√6712345解析 由题设条件可知△ABF2为等腰三角形,且AF2=BF2,
只要∠AF2B为钝角即可.故选B.675.过双曲线C: (a>0,b>0)的右焦点作一条与其渐近线平行的直线,交C于点P.若点P的横坐标为2a,则C的离心率为________.123456712345676.已知双曲线 (a>0,b>0)的左、右焦点分别为F1,F2,点M在双曲线的左支上,且|MF2|=7|MF1|,则此双曲线的离心率的最大值为____.12345解析 因为|MF2|=7|MF1|,
所以|MF2|-|MF1|=6|MF1|,
即2a=6|MF1|≥6(c-a),故8a≥6c,当且仅当M为双曲线的左顶点时,等号成立.677.已知椭圆C: (a>b>0)的左、右焦点分别为F1,F2,点P在椭圆C上,线段PF2与圆:x2+y2=b2相切于点Q,若Q是线段PF2的中点,e为C的离心率,则 的最小值是________.1234567解析 如图,连接PF1,OQ,由OQ为△PF1F2的中位线,由圆x2+y2=b2,
可得|OQ|=b,则|PF1|=2b.
由椭圆的定义可得|PF1|+|PF2|=2a,
即|PF2|=2a-2b.
又OQ⊥PF2,所以PF1⊥PF2,
即(2b)2+(2a-2b)2=(2c)2,
即b2+a2-2ab+b2=c2=a2-b2,12345671234567
