2020版高中数学新人教B版选修1-1第二章圆锥曲线与方程微专题突破三焦点弦的性质课件
文档属性
| 名称 | 2020版高中数学新人教B版选修1-1第二章圆锥曲线与方程微专题突破三焦点弦的性质课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-29 00:00:00 | ||
图片预览











文档简介
课件41张PPT。专题突破三 焦点弦的性质第二章 圆锥曲线与方程 抛物线的焦点弦是考试的热点,有关抛物线的焦点弦性质较为丰富,对抛物线焦点弦性质进行研究获得一些重要结论,往往能给解题带来新思路,有利于解题过程的优化.
一、焦点弦性质的推导
例1 抛物线y2=2px(p>0),设AB是抛物线的过焦点的一条弦(焦点弦),F是抛物线的焦点,A(x1,y1),B(x2,y2)(y1>0,y2<0),A,B在准线上的射影为A1,B1.②当AB的斜率存在时,设为k(k≠0),代入抛物线方程y2=2px,证明 当θ≠90°时,过A作AG⊥x轴,交x轴于G,由抛物线定义知|AF|=|AA1|,
在Rt△AFG中,|FG|=|AF|cos θ,
由图知|GG1|=|AA1|,当θ=90°时,可知|AF|=|BF|=p,证明 |AB|=|AF|+|BF|=x1+x2+p当且仅当θ=90°时取等号.
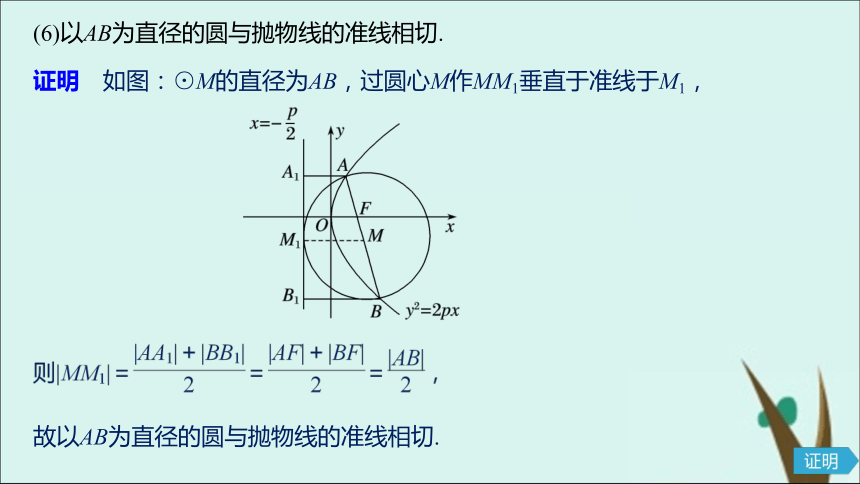
故通径长2p为最短的焦点弦长.证明 由(2)可得,(6)以AB为直径的圆与抛物线的准线相切.证明 如图:⊙M的直径为AB,过圆心M作MM1垂直于准线于M1,故以AB为直径的圆与抛物线的准线相切.二、焦点弦性质的应用
例2 (1)设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB的面积为√设A(x1,y1),B(x2,y2),(2)已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为
A.16 B.14 C.12 D.10√解析 方法一 抛物线C:y2=4x的焦点为F(1,0),
由题意可知l1,l2的斜率存在且不为0.
不妨设直线l1的斜率为k,同理得|DE|=4+4k2,故|AB|+|DE|的最小值为16.方法二 运用焦点弦的倾斜角公式,注意到两条弦互相垂直,点评 上述两道题目均是研究抛物线的焦点弦问题,涉及抛物线焦点弦长度与三角形面积,从高考客观题快速解答的要求来看,常规解法显然小题大做了,而利用焦点弦性质,可以快速解决此类小题.√解析 方法一 设点A(x1,y1),B(x2,y2),
由|AF|=3及抛物线定义可得,
x1+1=3,∴x1=2,√焦点坐标为(0,1).
设A,B,C,D,E的纵坐标分别为y1,y2,y3,y4,y5,∴y1-1+y2-1+y3-1+y4-1+y5-1=0,
∴y1+y2+y3+y4+y5=5,点评 用坐标表示向量,可以利用定义将向量的模长与坐标建立起联系.跟踪训练2 如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比为√12345√针对训练ZHENDUIXUNLIAN6781234567解析 如图所示,设AB的中点为P(x0,y0),分别过A,P,B三点作准线l的垂线,垂足分别为A′,Q,B′,
由题意得|AA′|+|BB′|=|AB|=4,812345√67812345√67812345√67解析 由焦点弦的性质知,
y1y2=-4,即|y1|·|y2|=4,当且仅当|y1|=|y2|=2时,取等号.85.如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于点C,若|BC|=3|BF|,且|AF|=4,则p的值为1234567√81234567解析 设直线l的倾斜角为θ,86.已知抛物线y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下顺次与上述两曲线交于点A,B,C,D(如图所示),则下列关于|AB|·|CD|的值的说法中,正确的是
A.等于1
B.等于4
C.最小值是1
D.最大值是41234567√8解析 设直线l:x=ty+1,
代入抛物线方程,得y2-4ty-4=0.
设A(x1,y1),D(x2,y2),
根据抛物线的定义知,
|AF|=x1+1,|DF|=x2+1,
故|AB|=x1,|CD|=x2,1234567而y1y2=-4,故|AB|·|CD|=1.87.设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点.若|AF|=3|BF|,则l的方程为
A.y=x-1或y=-x+11234567√812345678123456788.设抛物线的顶点在坐标原点,焦点F在y轴正半轴上,过点F的直线交抛物线于A,B两点,线段AB的长是8,AB的中点到x轴的距离是3.
(1)求抛物线的标准方程;解 设抛物线的方程是x2=2py(p>0),A(x1,y1),B(x2,y2),由抛物线定义可知y1+y2+p=8,
又AB的中点到x轴的距离为3,
∴y1+y2=6,∴p=2,
∴抛物线的标准方程是x2=4y.12345678(2)设直线m在y轴上的截距为6,且与抛物线交于P,Q两点.连接QF并延长交抛物线的准线于点R,当直线PR恰与抛物线相切时,求直线m的方程.12345678解 由题意知,直线m的斜率存在,设直线m:y=kx+6(k≠0),P(x3,y3),Q(x4,y4),12345678又Q,F,R三点共线,∴kQF=kFR,又F(0,1),整理得(x3x4)2-4[(x3+x4)2-2x3x4]+16+16x3x4=0,12345678
一、焦点弦性质的推导
例1 抛物线y2=2px(p>0),设AB是抛物线的过焦点的一条弦(焦点弦),F是抛物线的焦点,A(x1,y1),B(x2,y2)(y1>0,y2<0),A,B在准线上的射影为A1,B1.②当AB的斜率存在时,设为k(k≠0),代入抛物线方程y2=2px,证明 当θ≠90°时,过A作AG⊥x轴,交x轴于G,由抛物线定义知|AF|=|AA1|,
在Rt△AFG中,|FG|=|AF|cos θ,
由图知|GG1|=|AA1|,当θ=90°时,可知|AF|=|BF|=p,证明 |AB|=|AF|+|BF|=x1+x2+p当且仅当θ=90°时取等号.
故通径长2p为最短的焦点弦长.证明 由(2)可得,(6)以AB为直径的圆与抛物线的准线相切.证明 如图:⊙M的直径为AB,过圆心M作MM1垂直于准线于M1,故以AB为直径的圆与抛物线的准线相切.二、焦点弦性质的应用
例2 (1)设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB的面积为√设A(x1,y1),B(x2,y2),(2)已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为
A.16 B.14 C.12 D.10√解析 方法一 抛物线C:y2=4x的焦点为F(1,0),
由题意可知l1,l2的斜率存在且不为0.
不妨设直线l1的斜率为k,同理得|DE|=4+4k2,故|AB|+|DE|的最小值为16.方法二 运用焦点弦的倾斜角公式,注意到两条弦互相垂直,点评 上述两道题目均是研究抛物线的焦点弦问题,涉及抛物线焦点弦长度与三角形面积,从高考客观题快速解答的要求来看,常规解法显然小题大做了,而利用焦点弦性质,可以快速解决此类小题.√解析 方法一 设点A(x1,y1),B(x2,y2),
由|AF|=3及抛物线定义可得,
x1+1=3,∴x1=2,√焦点坐标为(0,1).
设A,B,C,D,E的纵坐标分别为y1,y2,y3,y4,y5,∴y1-1+y2-1+y3-1+y4-1+y5-1=0,
∴y1+y2+y3+y4+y5=5,点评 用坐标表示向量,可以利用定义将向量的模长与坐标建立起联系.跟踪训练2 如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比为√12345√针对训练ZHENDUIXUNLIAN6781234567解析 如图所示,设AB的中点为P(x0,y0),分别过A,P,B三点作准线l的垂线,垂足分别为A′,Q,B′,
由题意得|AA′|+|BB′|=|AB|=4,812345√67812345√67812345√67解析 由焦点弦的性质知,
y1y2=-4,即|y1|·|y2|=4,当且仅当|y1|=|y2|=2时,取等号.85.如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于点C,若|BC|=3|BF|,且|AF|=4,则p的值为1234567√81234567解析 设直线l的倾斜角为θ,86.已知抛物线y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下顺次与上述两曲线交于点A,B,C,D(如图所示),则下列关于|AB|·|CD|的值的说法中,正确的是
A.等于1
B.等于4
C.最小值是1
D.最大值是41234567√8解析 设直线l:x=ty+1,
代入抛物线方程,得y2-4ty-4=0.
设A(x1,y1),D(x2,y2),
根据抛物线的定义知,
|AF|=x1+1,|DF|=x2+1,
故|AB|=x1,|CD|=x2,1234567而y1y2=-4,故|AB|·|CD|=1.87.设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点.若|AF|=3|BF|,则l的方程为
A.y=x-1或y=-x+11234567√812345678123456788.设抛物线的顶点在坐标原点,焦点F在y轴正半轴上,过点F的直线交抛物线于A,B两点,线段AB的长是8,AB的中点到x轴的距离是3.
(1)求抛物线的标准方程;解 设抛物线的方程是x2=2py(p>0),A(x1,y1),B(x2,y2),由抛物线定义可知y1+y2+p=8,
又AB的中点到x轴的距离为3,
∴y1+y2=6,∴p=2,
∴抛物线的标准方程是x2=4y.12345678(2)设直线m在y轴上的截距为6,且与抛物线交于P,Q两点.连接QF并延长交抛物线的准线于点R,当直线PR恰与抛物线相切时,求直线m的方程.12345678解 由题意知,直线m的斜率存在,设直线m:y=kx+6(k≠0),P(x3,y3),Q(x4,y4),12345678又Q,F,R三点共线,∴kQF=kFR,又F(0,1),整理得(x3x4)2-4[(x3+x4)2-2x3x4]+16+16x3x4=0,12345678
