2020版高中数学新人教B版选修1-1第二章圆锥曲线与方程章末复习课件
文档属性
| 名称 | 2020版高中数学新人教B版选修1-1第二章圆锥曲线与方程章末复习课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-29 00:00:00 | ||
图片预览











文档简介
课件71张PPT。章末复习第二章 圆锥曲线与方程学习目标XUEXIMUBIAO1.梳理本章知识,构建知识网络.
2.进一步巩固和理解圆锥曲线的定义.
3.掌握圆锥曲线的几何性质,会利用几何性质解决相关问题.
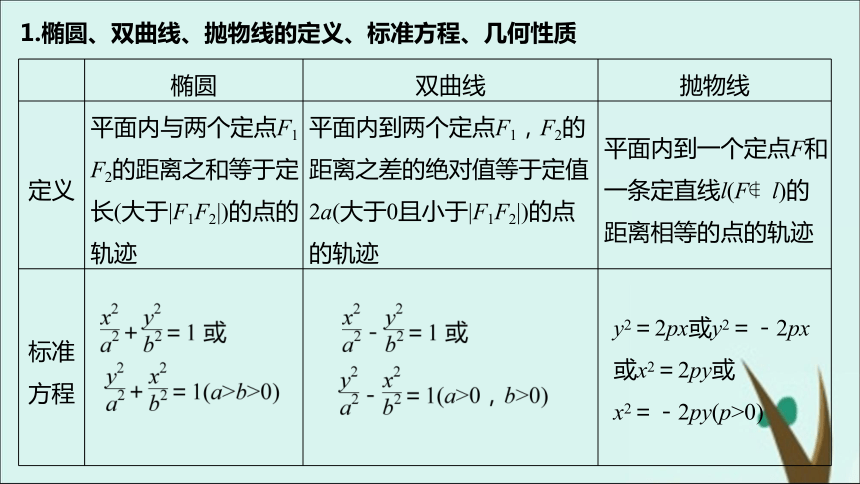
4.掌握简单的直线与圆锥曲线位置关系问题的解决方法.NEIRONGSUOYIN内容索引知识梳理题型探究达标检测1知识梳理PART ONE1.椭圆、双曲线、抛物线的定义、标准方程、几何性质y2=2px或y2=-2px
或x2=2py或
x2=-2py(p>0)2.椭圆的焦点三角形4.求圆锥曲线方程的一般步骤
一般求已知曲线类型的曲线方程问题,可采用“先定形,后定式,再定量”的步骤.
(1)定形——指的是二次曲线的焦点位置与对称轴的位置.
(2)定式——根据“形”设方程的形式,注意曲线系方程的应用,如当椭圆的焦点不确定在哪个坐标轴上时,可设方程为mx2+ny2=1(m>0,n>0且m≠n).
(3)定量——由题设中的条件找到“式”中待定系数的等量关系,通过解方程得到量的大小.5.直线与圆锥曲线的位置关系
(1)直线与双曲线、直线与抛物线有一个公共点应有两种情况:一是相切;二是直线与双曲线的渐近线平行、直线与抛物线的对称轴平行.
(2)直线与圆锥曲线的位置关系,涉及函数、方程、不等式、平面几何等诸多方面的知识,形成了求轨迹、最值、对称、取值范围、线段的长度等多种问题.解决此类问题应注意数形结合,以形辅数的方法;还要多结合圆锥曲线的定义,根与系数的关系以及“点差法”等.1.设A,B为两个定点,k为非零常数,|PA|-|PB|=k,则动点P的轨迹为双曲线.( )
2.若直线与曲线有一个公共点,则直线与曲线相切.( )
3.方程2x2-5x+2=0的两根x1,x2(x14.已知方程mx2+ny2=1,则当m>n时,该方程表示焦点在x轴上的椭圆.( )思考辨析 判断正误SIKAOBIANXIPANDUANZHENGWU×√××√2题型探究PART TWO题型一 圆锥曲线的定义及应用A.锐角三角形 B.直角三角形
C.钝角三角形 D.随m,n变化而变化√|F1F2|2=(2c)2=2(m+n),
而|PF1|2+|PF2|2=2(m+n)=(2c)2=|F1F2|2,
∴△F1PF2是直角三角形,故选B.解析 设P为双曲线右支上的一点.反思感悟 涉及椭圆、双曲线上的点与两个定点构成的三角形问题时,常用定义结合解三角形的知识来解决.跟踪训练1 抛物线y2=2px(p>0)上有A(x1,y1),B(x2,y2),C(x3,y3)三点,F是它的焦点,若|AF|,|BF|,|CF|成等差数列,则
A.x1,x2,x3成等差数列 B.y1,y2,y3成等差数列
C.x1,x3,x2成等差数列 D.y1,y3,y2成等差数列√故选A.解析 如图,过A,B,C分别作准线的垂线,垂足分别为A′,B′,C′,由抛物线定义可知|AF|=|AA′|,|BF|=|BB′|,|CF|=|CC′|.
∵2|BF|=|AF|+|CF|,
∴2|BB′|=|AA′|+|CC′|.题型二 圆锥曲线的方程及几何性质多维探究√反思感悟 一般求已知曲线类型的曲线方程问题,可采用“先定形,后定式,再定量”的步骤.
(1)定形——指的是二次曲线的焦点位置与对称轴的位置.
(2)定式——根据“形”设方程的形式,注意曲线系方程的应用,如当椭圆的焦点不确定在哪个坐标轴上时,可设方程为mx2+ny2=1(m>0,n>0且m≠n).
(3)定量——由题设中的条件找到“式”中待定系数的等量关系.跟踪训练2 设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点A(0,2),则C的方程为
A.y2=4x或y2=8x B.y2=2x或y2=8x
C.y2=4x或y2=16x D.y2=2x或y2=16x√因为圆心是MF的中点,所以抛物线C的方程为y2=4x或y2=16x.因为四边形AF1BF2为矩形,
所以|AF1|2+|AF2|2=|F1F2|2=12,
所以2|AF1||AF2|=(|AF1|+|AF2|)2-(|AF1|2+|AF2|2)=16-12=4,
所以(|AF2|-|AF1|)2=|AF1|2+|AF2|2-2|AF1|·|AF2|=12-4=8,反思感悟 求圆锥曲线离心率的三种方法
(1)定义法:由椭圆(双曲线)的标准方程可知,不论椭圆(双曲线)的焦点在x轴上还是在y轴上都有关系式a2-b2=c2(a2+b2=c2)以及e= ,已知其中的任意两个参数,可以求其他的参数,这是基本且常用的方法.
(2)方程法:建立参数a与c之间的齐次关系式,从而求出其离心率,这是求离心率的十分重要的思路及方法.
(3)几何法:求与过焦点的三角形有关的离心率问题,根据平面几何性质以及椭圆(双曲线)的定义、几何性质,建立参数之间的关系,通过画出图形,观察线段之间的关系,使问题更形象、直观.跟踪训练3 已知抛物线y2=4x的准线与双曲线 -y2=1交于A,B两点,点F为抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率是_____.解析 抛物线y2=4x的准线方程为x=-1,又△FAB为直角三角形,则只有∠AFB=90°,题型三 直线与圆锥曲线的位置关系(1)求椭圆的标准方程;所以b2=a2-c2=2-1=1,解 已知F2(1,0),直线斜率显然存在,
设直线的方程为y=(x-1),
A(x1,y1),B(x2,y2),化简得(1+2k2)x2-4k2x+2k2-2=0,
Δ=16k4-4(1+2k2)(2k2-2)>0,因为|MA|=|MB|,
所以点M在AB的中垂线上,②当k=0时,AB的中垂线方程为x=0,满足题意.反思感悟 解决圆锥曲线中的参数范围问题与求最值问题类似,一般有两种方法:
(1)函数法:用其他变量表示该参数,建立函数关系,利用求函数值域的方法求解.
(2)不等式法:根据题意建立含参数的不等关系式,通过解不等式求参数范围.(1)求椭圆E的标准方程;解 因为2c=2,所以c=1.所以b2=1,a2=2.(2)若直线y=kx+m与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.即x1x2+y1y2<0.
又y1y2=(kx1+m)(kx2+m)消去y,得(2k2+1)x2+4kmx+2m2-2=0,Δ=16k2-8m2+8>0,
即m2<2k2+1. (*)
因为原点O总在以PQ为直径的圆的内部,题型三 直线与圆锥曲线的位置关系(1)求椭圆的标准方程;所以b2=a2-c2=2-1=1,解 已知F2(1,0),直线斜率显然存在,
设直线的方程为y=(x-1),
A(x1,y1),B(x2,y2),化简得(1+2k2)x2-4k2x+2k2-2=0,
Δ=16k4-4(1+2k2)(2k2-2)>0,因为|MA|=|MB|,
所以点M在AB的中垂线上,②当k=0时,AB的中垂线方程为x=0,满足题意.反思感悟 解决圆锥曲线中的参数范围问题与求最值问题类似,一般有两种方法:
(1)函数法:用其他变量表示该参数,建立函数关系,利用求函数值域的方法求解.
(2)不等式法:根据题意建立含参数的不等关系式,通过解不等式求参数范围.(1)求椭圆E的标准方程;解 因为2c=2,所以c=1.所以b2=1,a2=2.(2)若直线y=kx+m与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.即x1x2+y1y2<0.
又y1y2=(kx1+m)(kx2+m)消去y,得(2k2+1)x2+4kmx+2m2-2=0,Δ=16k2-8m2+8>0,
即m2<2k2+1. (*)
因为原点O总在以PQ为直径的圆的内部,题型四 圆锥曲线中参数范围和最值问题(2)若抛物线x2=2y上距离点A(0,a)的最近点恰好是抛物线的顶点,则a的取值范围是
A.a>0 B.0C.a≤1 D.a≤0√反思感悟 圆锥曲线中最值与范围的求法有两种:
(1)几何法:若题目的条件和结论能明显体现几何图形特征及意义,则考虑利用图形性质来解决,这就是几何法.
(2)代数法:若题目的条件和结论能体现一种明确的函数关系,则可首先建立起目标函数,再求这个函数的最值与范围,求函数最值的常用方法有配方法、判别式法、重要不等式法及函数的单调性法等.①求满足上述条件的点M(x,y)的轨迹C的方程;∴a2-3b2=0,
∴x2+3y2=3,②设曲线C与直线y=kx+m(k≠0)相交于不同的两点P,Q,点A(0,-1),当|AP|=|AQ|时,求实数m的取值范围.得(1+3k2)x2+6kmx+3(m2-1)=0.
∵曲线C与直线y=kx+m(k≠0)相交于不同的两点,
∴Δ=(6km)2-12(1+3k2)(m2-1)=12(3k2-m2+1)>0,
即3k2-m2+1>0.
设P(x1,y1),Q(x2,y2),
线段PQ的中点N(x0,y0), ①∵|AP|=|AQ|,∴PQ⊥AN.
设kAN表示直线AN的斜率,
又k≠0,∴kAN·k=-1.得3k2=2m-1. ②将②代入①得2m-1-m2+1>0,即m2-2m<0,
解得0(1)求直线l的方程;解 由题意可得直线AB的斜率存在,且不为0.
设直线AB:x-2=m(y-2),
代入抛物线方程可得y2-8my+16m-16=0.
判别式Δ=(-8m)2-4(16m-16)=64(m2-m+1)>0恒成立.
设A(x1,y1),B(x2,y2),
则有y1+y2=8m,所以直线l的方程为2x-y-2=0.(2)抛物线上是否存在点C和D,使得C,D关于直线l对称?若存在,求出直线CD的方程;若不存在,请说明理由.解 假设C,D两点存在,其中Δ=(n+8)2-n2=16n+64>0,
则n>-4. (*)
又xC+xD=4(n+8),
所以CD的中点为(2(n+8),-8),代入直线l的方程,所以满足题意的C,D两点不存在.素养评析 (1)解决是否存在直线的问题时,可依据条件寻找适合条件的直线方程,联立方程消元得出一元二次方程,利用判别式得出是否有解.
(2)按照逻辑推理的形式与规则,探索论证结论的存在性,有助于培养学生的合乎逻辑的思想品质和理性精神.3达标检测PART THREE12345√所以c=1,b2=a2-c2=3-1=2,1234512345√1234√512345解析 ∵y2=8x的焦点为(2,0),∵c2=m2-n2=4,∴n2=12.12345√1234(1)求椭圆的方程;5(2)求弦长|CD|.解 ∵F1(-1,0),∴直线BF1的方程为y=-2x-2,设C(x1,y1),D(x2,y2),12345课堂小结KETANGXIAOJIE在解决圆锥曲线问题时,待定系数法,“设而不求”思想,转化与化归思想是最常用的几种思想方法,设而不求,在解决直线和圆锥曲线的位置关系问题中匠心独具,很好的解决了计算的烦琐问题.
2.进一步巩固和理解圆锥曲线的定义.
3.掌握圆锥曲线的几何性质,会利用几何性质解决相关问题.
4.掌握简单的直线与圆锥曲线位置关系问题的解决方法.NEIRONGSUOYIN内容索引知识梳理题型探究达标检测1知识梳理PART ONE1.椭圆、双曲线、抛物线的定义、标准方程、几何性质y2=2px或y2=-2px
或x2=2py或
x2=-2py(p>0)2.椭圆的焦点三角形4.求圆锥曲线方程的一般步骤
一般求已知曲线类型的曲线方程问题,可采用“先定形,后定式,再定量”的步骤.
(1)定形——指的是二次曲线的焦点位置与对称轴的位置.
(2)定式——根据“形”设方程的形式,注意曲线系方程的应用,如当椭圆的焦点不确定在哪个坐标轴上时,可设方程为mx2+ny2=1(m>0,n>0且m≠n).
(3)定量——由题设中的条件找到“式”中待定系数的等量关系,通过解方程得到量的大小.5.直线与圆锥曲线的位置关系
(1)直线与双曲线、直线与抛物线有一个公共点应有两种情况:一是相切;二是直线与双曲线的渐近线平行、直线与抛物线的对称轴平行.
(2)直线与圆锥曲线的位置关系,涉及函数、方程、不等式、平面几何等诸多方面的知识,形成了求轨迹、最值、对称、取值范围、线段的长度等多种问题.解决此类问题应注意数形结合,以形辅数的方法;还要多结合圆锥曲线的定义,根与系数的关系以及“点差法”等.1.设A,B为两个定点,k为非零常数,|PA|-|PB|=k,则动点P的轨迹为双曲线.( )
2.若直线与曲线有一个公共点,则直线与曲线相切.( )
3.方程2x2-5x+2=0的两根x1,x2(x1
C.钝角三角形 D.随m,n变化而变化√|F1F2|2=(2c)2=2(m+n),
而|PF1|2+|PF2|2=2(m+n)=(2c)2=|F1F2|2,
∴△F1PF2是直角三角形,故选B.解析 设P为双曲线右支上的一点.反思感悟 涉及椭圆、双曲线上的点与两个定点构成的三角形问题时,常用定义结合解三角形的知识来解决.跟踪训练1 抛物线y2=2px(p>0)上有A(x1,y1),B(x2,y2),C(x3,y3)三点,F是它的焦点,若|AF|,|BF|,|CF|成等差数列,则
A.x1,x2,x3成等差数列 B.y1,y2,y3成等差数列
C.x1,x3,x2成等差数列 D.y1,y3,y2成等差数列√故选A.解析 如图,过A,B,C分别作准线的垂线,垂足分别为A′,B′,C′,由抛物线定义可知|AF|=|AA′|,|BF|=|BB′|,|CF|=|CC′|.
∵2|BF|=|AF|+|CF|,
∴2|BB′|=|AA′|+|CC′|.题型二 圆锥曲线的方程及几何性质多维探究√反思感悟 一般求已知曲线类型的曲线方程问题,可采用“先定形,后定式,再定量”的步骤.
(1)定形——指的是二次曲线的焦点位置与对称轴的位置.
(2)定式——根据“形”设方程的形式,注意曲线系方程的应用,如当椭圆的焦点不确定在哪个坐标轴上时,可设方程为mx2+ny2=1(m>0,n>0且m≠n).
(3)定量——由题设中的条件找到“式”中待定系数的等量关系.跟踪训练2 设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点A(0,2),则C的方程为
A.y2=4x或y2=8x B.y2=2x或y2=8x
C.y2=4x或y2=16x D.y2=2x或y2=16x√因为圆心是MF的中点,所以抛物线C的方程为y2=4x或y2=16x.因为四边形AF1BF2为矩形,
所以|AF1|2+|AF2|2=|F1F2|2=12,
所以2|AF1||AF2|=(|AF1|+|AF2|)2-(|AF1|2+|AF2|2)=16-12=4,
所以(|AF2|-|AF1|)2=|AF1|2+|AF2|2-2|AF1|·|AF2|=12-4=8,反思感悟 求圆锥曲线离心率的三种方法
(1)定义法:由椭圆(双曲线)的标准方程可知,不论椭圆(双曲线)的焦点在x轴上还是在y轴上都有关系式a2-b2=c2(a2+b2=c2)以及e= ,已知其中的任意两个参数,可以求其他的参数,这是基本且常用的方法.
(2)方程法:建立参数a与c之间的齐次关系式,从而求出其离心率,这是求离心率的十分重要的思路及方法.
(3)几何法:求与过焦点的三角形有关的离心率问题,根据平面几何性质以及椭圆(双曲线)的定义、几何性质,建立参数之间的关系,通过画出图形,观察线段之间的关系,使问题更形象、直观.跟踪训练3 已知抛物线y2=4x的准线与双曲线 -y2=1交于A,B两点,点F为抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率是_____.解析 抛物线y2=4x的准线方程为x=-1,又△FAB为直角三角形,则只有∠AFB=90°,题型三 直线与圆锥曲线的位置关系(1)求椭圆的标准方程;所以b2=a2-c2=2-1=1,解 已知F2(1,0),直线斜率显然存在,
设直线的方程为y=(x-1),
A(x1,y1),B(x2,y2),化简得(1+2k2)x2-4k2x+2k2-2=0,
Δ=16k4-4(1+2k2)(2k2-2)>0,因为|MA|=|MB|,
所以点M在AB的中垂线上,②当k=0时,AB的中垂线方程为x=0,满足题意.反思感悟 解决圆锥曲线中的参数范围问题与求最值问题类似,一般有两种方法:
(1)函数法:用其他变量表示该参数,建立函数关系,利用求函数值域的方法求解.
(2)不等式法:根据题意建立含参数的不等关系式,通过解不等式求参数范围.(1)求椭圆E的标准方程;解 因为2c=2,所以c=1.所以b2=1,a2=2.(2)若直线y=kx+m与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.即x1x2+y1y2<0.
又y1y2=(kx1+m)(kx2+m)消去y,得(2k2+1)x2+4kmx+2m2-2=0,Δ=16k2-8m2+8>0,
即m2<2k2+1. (*)
因为原点O总在以PQ为直径的圆的内部,题型三 直线与圆锥曲线的位置关系(1)求椭圆的标准方程;所以b2=a2-c2=2-1=1,解 已知F2(1,0),直线斜率显然存在,
设直线的方程为y=(x-1),
A(x1,y1),B(x2,y2),化简得(1+2k2)x2-4k2x+2k2-2=0,
Δ=16k4-4(1+2k2)(2k2-2)>0,因为|MA|=|MB|,
所以点M在AB的中垂线上,②当k=0时,AB的中垂线方程为x=0,满足题意.反思感悟 解决圆锥曲线中的参数范围问题与求最值问题类似,一般有两种方法:
(1)函数法:用其他变量表示该参数,建立函数关系,利用求函数值域的方法求解.
(2)不等式法:根据题意建立含参数的不等关系式,通过解不等式求参数范围.(1)求椭圆E的标准方程;解 因为2c=2,所以c=1.所以b2=1,a2=2.(2)若直线y=kx+m与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.即x1x2+y1y2<0.
又y1y2=(kx1+m)(kx2+m)消去y,得(2k2+1)x2+4kmx+2m2-2=0,Δ=16k2-8m2+8>0,
即m2<2k2+1. (*)
因为原点O总在以PQ为直径的圆的内部,题型四 圆锥曲线中参数范围和最值问题(2)若抛物线x2=2y上距离点A(0,a)的最近点恰好是抛物线的顶点,则a的取值范围是
A.a>0 B.0
(1)几何法:若题目的条件和结论能明显体现几何图形特征及意义,则考虑利用图形性质来解决,这就是几何法.
(2)代数法:若题目的条件和结论能体现一种明确的函数关系,则可首先建立起目标函数,再求这个函数的最值与范围,求函数最值的常用方法有配方法、判别式法、重要不等式法及函数的单调性法等.①求满足上述条件的点M(x,y)的轨迹C的方程;∴a2-3b2=0,
∴x2+3y2=3,②设曲线C与直线y=kx+m(k≠0)相交于不同的两点P,Q,点A(0,-1),当|AP|=|AQ|时,求实数m的取值范围.得(1+3k2)x2+6kmx+3(m2-1)=0.
∵曲线C与直线y=kx+m(k≠0)相交于不同的两点,
∴Δ=(6km)2-12(1+3k2)(m2-1)=12(3k2-m2+1)>0,
即3k2-m2+1>0.
设P(x1,y1),Q(x2,y2),
线段PQ的中点N(x0,y0), ①∵|AP|=|AQ|,∴PQ⊥AN.
设kAN表示直线AN的斜率,
又k≠0,∴kAN·k=-1.得3k2=2m-1. ②将②代入①得2m-1-m2+1>0,即m2-2m<0,
解得0
设直线AB:x-2=m(y-2),
代入抛物线方程可得y2-8my+16m-16=0.
判别式Δ=(-8m)2-4(16m-16)=64(m2-m+1)>0恒成立.
设A(x1,y1),B(x2,y2),
则有y1+y2=8m,所以直线l的方程为2x-y-2=0.(2)抛物线上是否存在点C和D,使得C,D关于直线l对称?若存在,求出直线CD的方程;若不存在,请说明理由.解 假设C,D两点存在,其中Δ=(n+8)2-n2=16n+64>0,
则n>-4. (*)
又xC+xD=4(n+8),
所以CD的中点为(2(n+8),-8),代入直线l的方程,所以满足题意的C,D两点不存在.素养评析 (1)解决是否存在直线的问题时,可依据条件寻找适合条件的直线方程,联立方程消元得出一元二次方程,利用判别式得出是否有解.
(2)按照逻辑推理的形式与规则,探索论证结论的存在性,有助于培养学生的合乎逻辑的思想品质和理性精神.3达标检测PART THREE12345√所以c=1,b2=a2-c2=3-1=2,1234512345√1234√512345解析 ∵y2=8x的焦点为(2,0),∵c2=m2-n2=4,∴n2=12.12345√1234(1)求椭圆的方程;5(2)求弦长|CD|.解 ∵F1(-1,0),∴直线BF1的方程为y=-2x-2,设C(x1,y1),D(x2,y2),12345课堂小结KETANGXIAOJIE在解决圆锥曲线问题时,待定系数法,“设而不求”思想,转化与化归思想是最常用的几种思想方法,设而不求,在解决直线和圆锥曲线的位置关系问题中匠心独具,很好的解决了计算的烦琐问题.
