2018-2019学年江西省赣州市五校协作体高二(下)期中数学试卷(文科)
文档属性
| 名称 | 2018-2019学年江西省赣州市五校协作体高二(下)期中数学试卷(文科) |  | |
| 格式 | zip | ||
| 文件大小 | 102.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-29 14:53:25 | ||
图片预览




文档简介
2018-2019学年江西省赣州市五校协作体高二(下)期中数学试卷(文科)
一、选择题(本题共12小题,每小题5分)
1.已知全集U={1,2,3,4},集合A={1,2},B={2,3},则?U(A∩B)=( )
A.{1,3,4} B.{3,4} C.{3} D.{4}
2.已知复数,其中i为虚数单位,则|z|=( )
A. B. C. D.
3.若命题p:?x0∈R,2x02+1≤2,则该命题的否定是( )
A.?x0∈R,2x02+1>2 B.?x0∈R,2x02+1≥2
C.?x∈R,2x2+1≤2 D.?x∈R,2x2+1>2
4.“a=2”是“两直线ax+3y+2a=0和2x+(a+1)y﹣2=0平行”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.已知抛物线C:y2=2x上一点P到x轴的距离为2,则P到焦点的距离为( )
A.2 B. C. D.3
6.为了规定工时定额,需要确定加工某种零件所需的时间,为此进行了5次试验,得到5组数据:(x1,y1),(x2,y2),(x3,y3),(x4,y4),(x5,y5),由最小二乘法求得回归直线方程为=0.67x+54.9.若已知x1+x2+x3+x4+x5=150,则y1+y2+y3+y4+y5=( )
A.75 B.155.4 C.375 D.466.2
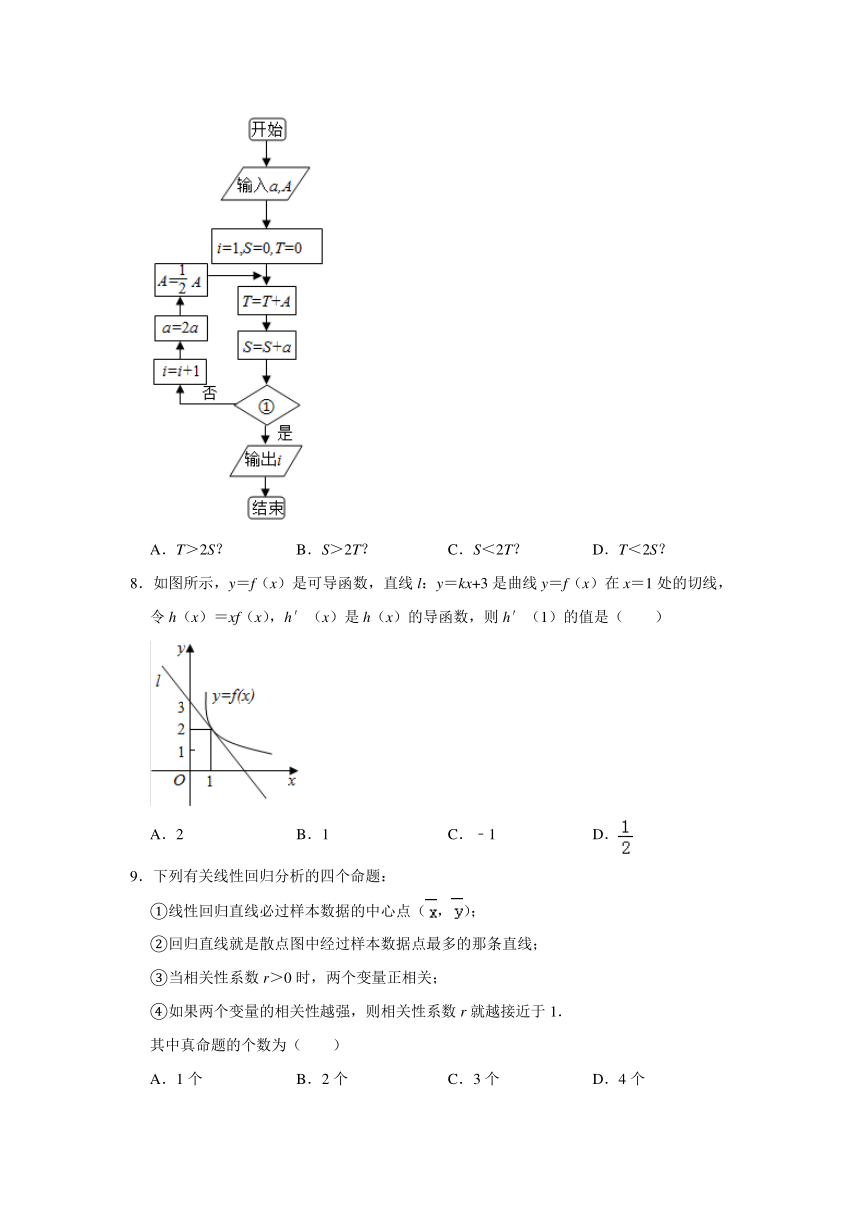
7.我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:
“今有蒲生一日,长三尺.莞生一日,长一尺.蒲生日自半.莞生日自倍.问几何日而长等?”(蒲常指一种多年生草本植物,莞指水葱一类的植物)
现欲知几日后,莞高超过蒲高一倍.为了解决这个新问题,设计右面的程序框图,输入A=3,a=1.那么在①处应填( )
A.T>2S? B.S>2T? C.S<2T? D.T<2S?
8.如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,令h(x)=xf(x),h′(x)是h(x)的导函数,则h′(1)的值是( )
A.2 B.1 C.﹣1 D.
9.下列有关线性回归分析的四个命题:
①线性回归直线必过样本数据的中心点(,);
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数r>0时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数r就越接近于1.
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
10.已知双曲线C:=1(a>0,b>0)的焦点F(2,0)到渐近线的距离为,则该双曲线的离心率为( )
A.1 B. C.2 D.2
11.已知函数f(x)=x3+ax2+bx﹣a2﹣7a在x=1处取得极大值10,则的值为( )
A. B.﹣2 C.﹣2或 D.不存在
12.将正整数排列如图:则图中数2019出现在( )
A.第44行第84列 B.第45行第84列
C.第44行第83列 D.第45行第83列
二、填空题(本题共4小题,每小题5分)
13.在极坐标系中,圆C:ρ=2sinθ的圆心到点(1,0)的距离为 .
14.甲、乙、丙三人中,只有一个会弹钢琴.甲说:“我会”,乙说:“我不会”,丙说:“甲不会”.如果这三句话只有一句是真的,那么会弹钢琴的是 .
15.抛物线x2=2py(p>0)的焦点为F,其准线与双曲线x2﹣y2=1相交于A,B两点,若△ABF为等边三角形,则p= .
16.曲线在点(1,f(1))处的切线的斜率为 .
三、解答题(解答应写出文字说明、证明过程或演算步骤)
17.(10分)已知双曲线C的标准方程为 ﹣=1.
(1)写出双曲线C的实轴长,虚轴长,离心率,左、右焦点F1、F2的坐标;
(2)若点M(3,m)在双曲线C上,求证:MF1⊥MF2.
18.(12分)某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出f(5);
(2)利用合情推理的“归纳推理思想”归纳出f(n+1)与f(n)的关系式,并根据你得到的关系式求f(n)的表达式;
(3)求+++…+的值.
19.(12分)到2020年,我国将全面建立起新的高考制度,新高考采用3+3模式,其中语文、数学、英语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣、爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门(6选3)参加考试,满分各100分.为了顺利迎接新高考改革,某学校采用分层抽样的方法从高一年级1000名(其中男生550名,女生450名)学生中抽取了n名学生进行调查.
(1)已知抽取的n名学生中有女生45名,求n的值及抽取的男生的人数.
(2)该校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的n名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目,且只能选择一个科目),得到如下2×2列联表.
选择“物理”
选择“地理”
总计
男生
10
女生
25
总计
(i)请将列联表补充完整,并判断是否有99%以上的把握认为选择科目与性别有关系.
(ii)在抽取的选择“地理”的学生中按性别分层抽样抽取6名,再从这6名学生中抽取2名,求这2名中至少有1名男生的概率.
附:K2=,其中n=a+b+c+d.
P(K2≥k0)
0.05
0.01
k0
3.841
6.635
20.(12分)已知函数f(x)=x2(x﹣1).
(1)求函数f(x)的单调区间;
(2)求f(x)在区间[﹣1,2]上的最大值和最小值.
21.(12分)已知椭圆C:=1(a>b>0),O为坐标原点,F(﹣)为椭圆C的左焦点,离心率为,直线l与椭圆相交于A,B两点.
(1)求椭圆C的方程;
(2)若M(1,1)是弦AB的中点,P是椭圆C上一点,求△PAB的面积最大值.
22.(12分)已知函数f(x)=﹣2a2lnx+x2+ax(a∈R).
(1)当a=1时,求曲线y=f(x)在(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性;
(3)当a<0时,求函数f(x)在区间[1,e]的最小值.
2018-2019学年江西省赣州市五校协作体高二(下)期中数学试卷(文科)
参考答案与试题解析
一、选择题(本题共12小题,每小题5分)
1.【解答】解:∵集合A={1,2},B={2,3},∴A∩B={2},
由全集U={1,2,3,4},
∴?U(A∩B)={1,3,4}.
故选:A.
2.【解答】解:∵,
∴|z|=||=.
故选:C.
3.【解答】解:由特称命题的否定可知:
命题p的否定是“?x∈R,2x2+1>2,
故选:D.
4.【解答】解:两直线ax+3y+2a=0和2x+(a+1)y﹣2=0平行的充要条件为,即a=2或a=﹣3,
又“a=2”是“a=2或a=﹣3的充分不必要条件,
即“a=2”是“两直线ax+3y+2a=0和2x+(a+1)y﹣2=0平行”的充分不必要条件,
故选:A.
5.【解答】解:抛物线C:y2=2x上一点P到x轴的距离为2,可得P(2,±2),
抛物线的准线方程为:x=﹣,
则P到焦点的距离为:2+=.
故选:C.
6.【解答】解:(1)=,回归直线方程为=0.67x+54.9.
可得:=0.67×30+54.8≈75.
则y1+y2+y3+y4+y5=?n=75×5=375.
故选:C.
7.【解答】解:由题意,S表示莞高,T表示蒲高,现欲知几日后,莞高超过蒲高一倍,故①处应填S>2T?.
故选:B.
8.【解答】解:由图象可知直线的切线经过点(1,2),则k+3=2,得k=﹣1,
即f′(1)=﹣1,且f(1)=2,
∵h(x)=xf(x),
∴h′(x)=f(x)+xf′(x),
则h′(1)=f(1)+f′(1)=2﹣1=1,
故选:B.
9.【解答】解:①线性回归直线必过样本数据的中心点(,),故①正确;
②回归直线在散点图中可能不经过任一样本数据点,故②错误;
③当相关性系数r>0时,则两个变量正相关,故③正确;
④如果两个变量的相关性越强,则相关性系数r就越接近于1或﹣1,故④错误.
故真命题的个数为2个,
故选:B.
10.【解答】解:双曲线C:=1(a>0,b>0)的焦点F(2,0)到渐近线的距离为,则,
∴c=2,b=,∴a2=c2﹣b2=4﹣3=1,∴a=1,
双曲线的离心率为:=2.
故选:C.
11.【解答】解:∵f(x)=x3+ax2+bx﹣a2﹣7a,
∴f′(x)=3x2+2ax+b,
又f(x)=x3+ax2+bx﹣a2﹣7a在x=1处取得极大值10,
∴f′(1)=3+2a+b=0,f(1)=1+a+b﹣a2﹣7a=10,
∴a2+8a+12=0,
∴a=﹣2,b=1或a=﹣6,b=9.
当a=﹣2,b=1时,f′(x)=3x2﹣4x+1=(3x﹣1)(x﹣1),
当<x<1时,f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在x=1处取得极小值,与题意不符;
当a=﹣6,b=9时,f′(x)=3x2﹣12x+9=3(x﹣1)(x﹣3)
当x<1时,f′(x)>0,当1<x<3时,f′(x)<0,
∴f(x)在x=1处取得极大值,符合题意;
∴=﹣=﹣.
故选:A.
12.【解答】解:依题意,经过观察,第n行的最后一个数为n2,而令n2≤2019得,n≤44,
所以2019在第45行,2019﹣442=83,
所以2019 在第45行,第83列.
故选:D.
二、填空题(本题共4小题,每小题5分)
13.【解答】解:在圆C的极坐标方程两边同时乘以ρ得,ρ2=2ρsinθ,化为普通方程得x2+y2=2y,即x2+(y﹣1)2=1,
所以,圆C的圆心为C(0,1),该圆心到点(1,0)的距离为.
故答案为:.
14.【解答】解:①设会弹钢琴的是甲,则甲、乙说的是真话,与题设矛盾,故会弹钢琴的不是甲,
②设会弹钢琴的是乙,则丙说的是真话,与题设相符,故会弹钢琴的是乙,
③设会弹钢琴的是丙,则乙、丙说的时真话,与题设矛盾,故会弹钢琴的不是丙,
综合①②③得:会弹钢琴的是乙,
故答案为:乙
15.【解答】解:抛物线的焦点坐标为(0,),准线方程为:y=﹣,
准线方程与双曲线x2﹣y2=1联立可得:x2﹣()2=1,
解得x=±,
因为△ABF为等边三角形,所以=2|x|,即p2=3x2,
即p2=3(),解得p=2.
故答案为:.
16.【解答】解:曲线,可得y′=,
所以曲线在点(1,f(1))处的切线的斜率为:=e+1.
故答案为:e+1.
三、解答题(解答应写出文字说明、证明过程或演算步骤)
17.【解答】解:(1)由双曲线C的标准方程为 ﹣=1,则a=,b=,c===2,
则实轴长,虚轴长,离心率,左、右焦点F1、F2(8分)
(2)证明::∵=(﹣3﹣2,﹣m),=(2﹣3,﹣m),
∴?=(﹣3﹣2)×(2﹣3)+m2=﹣3+m2,
由M在双曲线C上,则9﹣m2=6,即m2﹣3=0,
即?=0,
所以MF1⊥MF2(12分)
18.【解答】解:(1)∵f(1)=1,f(2)=1+4=5,f(3)=1+4+8=13,f(4)=1+4+8+12=25,
∴f(5)=1+4+8+12+16=41.
(2)∵f(2)﹣f(1)=4=4×1,
f(3)﹣f(2)=8=4×2,
f(4)﹣f(3)=12=4×3,
f(5)﹣f(4)=16=4×4,
由上式规律得出f(n+1)﹣f(n)=4n.
∴f(n)﹣f(n﹣1)=4(n﹣1),
f(n﹣1)﹣f(n﹣2)=4?(n﹣2),
f(n﹣2)﹣f(n﹣3)=4?(n﹣3),
…
f(2)﹣f(1)=4×1,
∴f(n)﹣f(1)=4[(n﹣1)+(n﹣2)+…+2+1]
=2(n﹣1)?n,
∴f(n)=2n2﹣2n+1.
(3)当n≥2时,==(﹣),
∴+++…+=1+(1﹣+﹣+…+﹣)=1+(1﹣)=﹣.
19.【解答】解:(1)由题意得解得n=100,则抽取的男生的人数为550×=55.
(2)(i)
选择“物理”
选择“地理”
总计
男生
45
10
55
女生
25
20
45
总计
70
30
100
则K2=≈8.1289>6.635.
所以有99%以上的把握认为选送科目与性别有关.
(ii)由题意易知抽取的选择“地理”的6名学生中,有2名男生,分别记为A,B,4名女生,分别记为a,b,c,d;
从6名学生中抽取2名,有AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,ab,ac,ad,bc,bd,cd共15种情况,
其中至少有1名男生的有AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd共9种情况,
故所求概率为.
20.【解答】解:(1)令f′(x)=3x2﹣2x>0,可得x<0或x>,
令f′(x)<0,解得::0<x<,
所以f(x)的递增区间为(﹣∞,0),(,+∞),递减区间为(0,).
(2)由(1)知:x=0,分别是f(x)的极大值点和极小值点,
所以f(x)极大值=f(0)=0,f(x)极小值=f()=﹣,
而f(﹣1)=﹣2,f(2)=4,
所以f(x)最大值=f(2)=4,f(x)最小值=f(﹣1)=﹣2.
21.【解答】解:(1)∵圆C:=1(a>b>0),O为坐标原点,F(﹣)为椭圆C的左焦点,离心率为,
∴,解得a=2,b=c=,
∴椭圆C的方程为:=1.
(2)设A(x1,y1),B(x2,y2).
∵M(1,1)是弦AB的中点,∴直线l的斜率存在,设斜率为k,
则直线l的方程为:y﹣1=k(x﹣1),即y=kx+1﹣k.
由联立,整理得:(1+2k2)x2+4k(1﹣k)x+2(1﹣k2)﹣4=0,
∵直线与椭圆相交,∴△>0成立.
∴,x1x2=,
∴=2,∴k=﹣,
∴直线l的方程为:x+2y﹣3=0,x1+x2=2,x1x2=,
∴|AB|=?|x1﹣x2|=?==.
要使△PAB的面积最大值,而|AB|是定值,需P点到AB的距离最大即可.
设与直线l平行的直线方程为:x+2y+m=0,
由方程组联立,得6y2+4my+m2﹣4=0,
令△16m2﹣24(m2﹣4)=0,得m=.
∵P是椭圆C上一点,
∴P点到AB的最大距离,即直线x+2y+2=0到直线l的距离d.
而d==,
此时==.
∴△PAB的面积最大值为.
22.【解答】解:(1)当a=1时,f(x)=﹣2lnx+x2+x,f′(x)=(x>0).
∴f′(1)=0,又f(1)=,
∴曲线y=f(x)在(1,f(1))处的切线方程为y=;
(2)f′(x)==(x>0).
当a=0时,f′(x)=x>0,f(x)在(0,+∞)上为增函数;
当a<0时,在x∈(0,﹣2a)上有f′(x)<0,当x∈(﹣2a,+∞)上,有f′(x)>0,
∴f(x)的减区间为(0,﹣2a),增区间为(﹣2a,+∞);
当a>0时,在x∈(0,a)上有f′(x)<0,当x∈(a,+∞)上,有f′(x)>0,
∴f(x)的减区间为(0,a),增区间为(a,+∞);
(3)由(2)知,当a<0时,f(x)的减区间为(0,﹣2a),增区间为(﹣2a,+∞),
若﹣2a≤1,即﹣<0时,f(x)在[1,e]单调递增,;
若1<﹣2a<e,即,f(x)在(1,﹣2a)上单调递减,在(﹣2a,e)上单调递增,;
若﹣2a≥e,即a时,f(x)在[1,e]单调递减,.
综上,.
一、选择题(本题共12小题,每小题5分)
1.已知全集U={1,2,3,4},集合A={1,2},B={2,3},则?U(A∩B)=( )
A.{1,3,4} B.{3,4} C.{3} D.{4}
2.已知复数,其中i为虚数单位,则|z|=( )
A. B. C. D.
3.若命题p:?x0∈R,2x02+1≤2,则该命题的否定是( )
A.?x0∈R,2x02+1>2 B.?x0∈R,2x02+1≥2
C.?x∈R,2x2+1≤2 D.?x∈R,2x2+1>2
4.“a=2”是“两直线ax+3y+2a=0和2x+(a+1)y﹣2=0平行”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.已知抛物线C:y2=2x上一点P到x轴的距离为2,则P到焦点的距离为( )
A.2 B. C. D.3
6.为了规定工时定额,需要确定加工某种零件所需的时间,为此进行了5次试验,得到5组数据:(x1,y1),(x2,y2),(x3,y3),(x4,y4),(x5,y5),由最小二乘法求得回归直线方程为=0.67x+54.9.若已知x1+x2+x3+x4+x5=150,则y1+y2+y3+y4+y5=( )
A.75 B.155.4 C.375 D.466.2
7.我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:
“今有蒲生一日,长三尺.莞生一日,长一尺.蒲生日自半.莞生日自倍.问几何日而长等?”(蒲常指一种多年生草本植物,莞指水葱一类的植物)
现欲知几日后,莞高超过蒲高一倍.为了解决这个新问题,设计右面的程序框图,输入A=3,a=1.那么在①处应填( )
A.T>2S? B.S>2T? C.S<2T? D.T<2S?
8.如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,令h(x)=xf(x),h′(x)是h(x)的导函数,则h′(1)的值是( )
A.2 B.1 C.﹣1 D.
9.下列有关线性回归分析的四个命题:
①线性回归直线必过样本数据的中心点(,);
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数r>0时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数r就越接近于1.
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
10.已知双曲线C:=1(a>0,b>0)的焦点F(2,0)到渐近线的距离为,则该双曲线的离心率为( )
A.1 B. C.2 D.2
11.已知函数f(x)=x3+ax2+bx﹣a2﹣7a在x=1处取得极大值10,则的值为( )
A. B.﹣2 C.﹣2或 D.不存在
12.将正整数排列如图:则图中数2019出现在( )
A.第44行第84列 B.第45行第84列
C.第44行第83列 D.第45行第83列
二、填空题(本题共4小题,每小题5分)
13.在极坐标系中,圆C:ρ=2sinθ的圆心到点(1,0)的距离为 .
14.甲、乙、丙三人中,只有一个会弹钢琴.甲说:“我会”,乙说:“我不会”,丙说:“甲不会”.如果这三句话只有一句是真的,那么会弹钢琴的是 .
15.抛物线x2=2py(p>0)的焦点为F,其准线与双曲线x2﹣y2=1相交于A,B两点,若△ABF为等边三角形,则p= .
16.曲线在点(1,f(1))处的切线的斜率为 .
三、解答题(解答应写出文字说明、证明过程或演算步骤)
17.(10分)已知双曲线C的标准方程为 ﹣=1.
(1)写出双曲线C的实轴长,虚轴长,离心率,左、右焦点F1、F2的坐标;
(2)若点M(3,m)在双曲线C上,求证:MF1⊥MF2.
18.(12分)某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出f(5);
(2)利用合情推理的“归纳推理思想”归纳出f(n+1)与f(n)的关系式,并根据你得到的关系式求f(n)的表达式;
(3)求+++…+的值.
19.(12分)到2020年,我国将全面建立起新的高考制度,新高考采用3+3模式,其中语文、数学、英语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣、爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门(6选3)参加考试,满分各100分.为了顺利迎接新高考改革,某学校采用分层抽样的方法从高一年级1000名(其中男生550名,女生450名)学生中抽取了n名学生进行调查.
(1)已知抽取的n名学生中有女生45名,求n的值及抽取的男生的人数.
(2)该校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的n名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目,且只能选择一个科目),得到如下2×2列联表.
选择“物理”
选择“地理”
总计
男生
10
女生
25
总计
(i)请将列联表补充完整,并判断是否有99%以上的把握认为选择科目与性别有关系.
(ii)在抽取的选择“地理”的学生中按性别分层抽样抽取6名,再从这6名学生中抽取2名,求这2名中至少有1名男生的概率.
附:K2=,其中n=a+b+c+d.
P(K2≥k0)
0.05
0.01
k0
3.841
6.635
20.(12分)已知函数f(x)=x2(x﹣1).
(1)求函数f(x)的单调区间;
(2)求f(x)在区间[﹣1,2]上的最大值和最小值.
21.(12分)已知椭圆C:=1(a>b>0),O为坐标原点,F(﹣)为椭圆C的左焦点,离心率为,直线l与椭圆相交于A,B两点.
(1)求椭圆C的方程;
(2)若M(1,1)是弦AB的中点,P是椭圆C上一点,求△PAB的面积最大值.
22.(12分)已知函数f(x)=﹣2a2lnx+x2+ax(a∈R).
(1)当a=1时,求曲线y=f(x)在(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性;
(3)当a<0时,求函数f(x)在区间[1,e]的最小值.
2018-2019学年江西省赣州市五校协作体高二(下)期中数学试卷(文科)
参考答案与试题解析
一、选择题(本题共12小题,每小题5分)
1.【解答】解:∵集合A={1,2},B={2,3},∴A∩B={2},
由全集U={1,2,3,4},
∴?U(A∩B)={1,3,4}.
故选:A.
2.【解答】解:∵,
∴|z|=||=.
故选:C.
3.【解答】解:由特称命题的否定可知:
命题p的否定是“?x∈R,2x2+1>2,
故选:D.
4.【解答】解:两直线ax+3y+2a=0和2x+(a+1)y﹣2=0平行的充要条件为,即a=2或a=﹣3,
又“a=2”是“a=2或a=﹣3的充分不必要条件,
即“a=2”是“两直线ax+3y+2a=0和2x+(a+1)y﹣2=0平行”的充分不必要条件,
故选:A.
5.【解答】解:抛物线C:y2=2x上一点P到x轴的距离为2,可得P(2,±2),
抛物线的准线方程为:x=﹣,
则P到焦点的距离为:2+=.
故选:C.
6.【解答】解:(1)=,回归直线方程为=0.67x+54.9.
可得:=0.67×30+54.8≈75.
则y1+y2+y3+y4+y5=?n=75×5=375.
故选:C.
7.【解答】解:由题意,S表示莞高,T表示蒲高,现欲知几日后,莞高超过蒲高一倍,故①处应填S>2T?.
故选:B.
8.【解答】解:由图象可知直线的切线经过点(1,2),则k+3=2,得k=﹣1,
即f′(1)=﹣1,且f(1)=2,
∵h(x)=xf(x),
∴h′(x)=f(x)+xf′(x),
则h′(1)=f(1)+f′(1)=2﹣1=1,
故选:B.
9.【解答】解:①线性回归直线必过样本数据的中心点(,),故①正确;
②回归直线在散点图中可能不经过任一样本数据点,故②错误;
③当相关性系数r>0时,则两个变量正相关,故③正确;
④如果两个变量的相关性越强,则相关性系数r就越接近于1或﹣1,故④错误.
故真命题的个数为2个,
故选:B.
10.【解答】解:双曲线C:=1(a>0,b>0)的焦点F(2,0)到渐近线的距离为,则,
∴c=2,b=,∴a2=c2﹣b2=4﹣3=1,∴a=1,
双曲线的离心率为:=2.
故选:C.
11.【解答】解:∵f(x)=x3+ax2+bx﹣a2﹣7a,
∴f′(x)=3x2+2ax+b,
又f(x)=x3+ax2+bx﹣a2﹣7a在x=1处取得极大值10,
∴f′(1)=3+2a+b=0,f(1)=1+a+b﹣a2﹣7a=10,
∴a2+8a+12=0,
∴a=﹣2,b=1或a=﹣6,b=9.
当a=﹣2,b=1时,f′(x)=3x2﹣4x+1=(3x﹣1)(x﹣1),
当<x<1时,f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在x=1处取得极小值,与题意不符;
当a=﹣6,b=9时,f′(x)=3x2﹣12x+9=3(x﹣1)(x﹣3)
当x<1时,f′(x)>0,当1<x<3时,f′(x)<0,
∴f(x)在x=1处取得极大值,符合题意;
∴=﹣=﹣.
故选:A.
12.【解答】解:依题意,经过观察,第n行的最后一个数为n2,而令n2≤2019得,n≤44,
所以2019在第45行,2019﹣442=83,
所以2019 在第45行,第83列.
故选:D.
二、填空题(本题共4小题,每小题5分)
13.【解答】解:在圆C的极坐标方程两边同时乘以ρ得,ρ2=2ρsinθ,化为普通方程得x2+y2=2y,即x2+(y﹣1)2=1,
所以,圆C的圆心为C(0,1),该圆心到点(1,0)的距离为.
故答案为:.
14.【解答】解:①设会弹钢琴的是甲,则甲、乙说的是真话,与题设矛盾,故会弹钢琴的不是甲,
②设会弹钢琴的是乙,则丙说的是真话,与题设相符,故会弹钢琴的是乙,
③设会弹钢琴的是丙,则乙、丙说的时真话,与题设矛盾,故会弹钢琴的不是丙,
综合①②③得:会弹钢琴的是乙,
故答案为:乙
15.【解答】解:抛物线的焦点坐标为(0,),准线方程为:y=﹣,
准线方程与双曲线x2﹣y2=1联立可得:x2﹣()2=1,
解得x=±,
因为△ABF为等边三角形,所以=2|x|,即p2=3x2,
即p2=3(),解得p=2.
故答案为:.
16.【解答】解:曲线,可得y′=,
所以曲线在点(1,f(1))处的切线的斜率为:=e+1.
故答案为:e+1.
三、解答题(解答应写出文字说明、证明过程或演算步骤)
17.【解答】解:(1)由双曲线C的标准方程为 ﹣=1,则a=,b=,c===2,
则实轴长,虚轴长,离心率,左、右焦点F1、F2(8分)
(2)证明::∵=(﹣3﹣2,﹣m),=(2﹣3,﹣m),
∴?=(﹣3﹣2)×(2﹣3)+m2=﹣3+m2,
由M在双曲线C上,则9﹣m2=6,即m2﹣3=0,
即?=0,
所以MF1⊥MF2(12分)
18.【解答】解:(1)∵f(1)=1,f(2)=1+4=5,f(3)=1+4+8=13,f(4)=1+4+8+12=25,
∴f(5)=1+4+8+12+16=41.
(2)∵f(2)﹣f(1)=4=4×1,
f(3)﹣f(2)=8=4×2,
f(4)﹣f(3)=12=4×3,
f(5)﹣f(4)=16=4×4,
由上式规律得出f(n+1)﹣f(n)=4n.
∴f(n)﹣f(n﹣1)=4(n﹣1),
f(n﹣1)﹣f(n﹣2)=4?(n﹣2),
f(n﹣2)﹣f(n﹣3)=4?(n﹣3),
…
f(2)﹣f(1)=4×1,
∴f(n)﹣f(1)=4[(n﹣1)+(n﹣2)+…+2+1]
=2(n﹣1)?n,
∴f(n)=2n2﹣2n+1.
(3)当n≥2时,==(﹣),
∴+++…+=1+(1﹣+﹣+…+﹣)=1+(1﹣)=﹣.
19.【解答】解:(1)由题意得解得n=100,则抽取的男生的人数为550×=55.
(2)(i)
选择“物理”
选择“地理”
总计
男生
45
10
55
女生
25
20
45
总计
70
30
100
则K2=≈8.1289>6.635.
所以有99%以上的把握认为选送科目与性别有关.
(ii)由题意易知抽取的选择“地理”的6名学生中,有2名男生,分别记为A,B,4名女生,分别记为a,b,c,d;
从6名学生中抽取2名,有AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,ab,ac,ad,bc,bd,cd共15种情况,
其中至少有1名男生的有AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd共9种情况,
故所求概率为.
20.【解答】解:(1)令f′(x)=3x2﹣2x>0,可得x<0或x>,
令f′(x)<0,解得::0<x<,
所以f(x)的递增区间为(﹣∞,0),(,+∞),递减区间为(0,).
(2)由(1)知:x=0,分别是f(x)的极大值点和极小值点,
所以f(x)极大值=f(0)=0,f(x)极小值=f()=﹣,
而f(﹣1)=﹣2,f(2)=4,
所以f(x)最大值=f(2)=4,f(x)最小值=f(﹣1)=﹣2.
21.【解答】解:(1)∵圆C:=1(a>b>0),O为坐标原点,F(﹣)为椭圆C的左焦点,离心率为,
∴,解得a=2,b=c=,
∴椭圆C的方程为:=1.
(2)设A(x1,y1),B(x2,y2).
∵M(1,1)是弦AB的中点,∴直线l的斜率存在,设斜率为k,
则直线l的方程为:y﹣1=k(x﹣1),即y=kx+1﹣k.
由联立,整理得:(1+2k2)x2+4k(1﹣k)x+2(1﹣k2)﹣4=0,
∵直线与椭圆相交,∴△>0成立.
∴,x1x2=,
∴=2,∴k=﹣,
∴直线l的方程为:x+2y﹣3=0,x1+x2=2,x1x2=,
∴|AB|=?|x1﹣x2|=?==.
要使△PAB的面积最大值,而|AB|是定值,需P点到AB的距离最大即可.
设与直线l平行的直线方程为:x+2y+m=0,
由方程组联立,得6y2+4my+m2﹣4=0,
令△16m2﹣24(m2﹣4)=0,得m=.
∵P是椭圆C上一点,
∴P点到AB的最大距离,即直线x+2y+2=0到直线l的距离d.
而d==,
此时==.
∴△PAB的面积最大值为.
22.【解答】解:(1)当a=1时,f(x)=﹣2lnx+x2+x,f′(x)=(x>0).
∴f′(1)=0,又f(1)=,
∴曲线y=f(x)在(1,f(1))处的切线方程为y=;
(2)f′(x)==(x>0).
当a=0时,f′(x)=x>0,f(x)在(0,+∞)上为增函数;
当a<0时,在x∈(0,﹣2a)上有f′(x)<0,当x∈(﹣2a,+∞)上,有f′(x)>0,
∴f(x)的减区间为(0,﹣2a),增区间为(﹣2a,+∞);
当a>0时,在x∈(0,a)上有f′(x)<0,当x∈(a,+∞)上,有f′(x)>0,
∴f(x)的减区间为(0,a),增区间为(a,+∞);
(3)由(2)知,当a<0时,f(x)的减区间为(0,﹣2a),增区间为(﹣2a,+∞),
若﹣2a≤1,即﹣<0时,f(x)在[1,e]单调递增,;
若1<﹣2a<e,即,f(x)在(1,﹣2a)上单调递减,在(﹣2a,e)上单调递增,;
若﹣2a≥e,即a时,f(x)在[1,e]单调递减,.
综上,.
同课章节目录
