8.2.2 不等式的简单变形 课件(共15张PPT)
文档属性
| 名称 | 8.2.2 不等式的简单变形 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 302.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 00:00:00 | ||
图片预览




文档简介
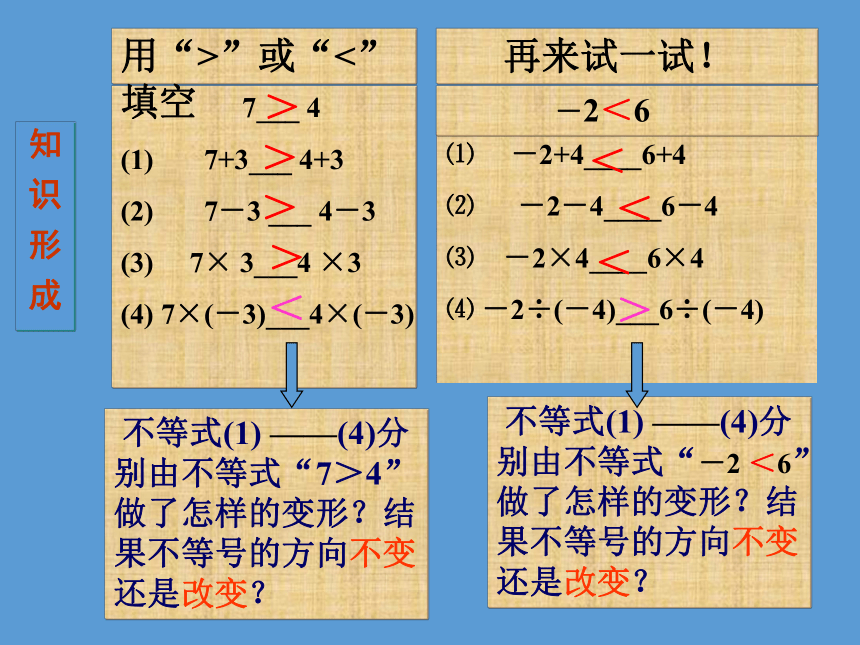
课件15张PPT。 不等式的简单变形等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.(2)等式的两边都乘以(或除以)同一个数(除数不能为零),所得的结果仍是等式.复习引入⑴ -2+4____6+4
⑵ -2-4____6-4
⑶ -2×4____6×4
⑷ -2÷(-4)___6÷(-4)
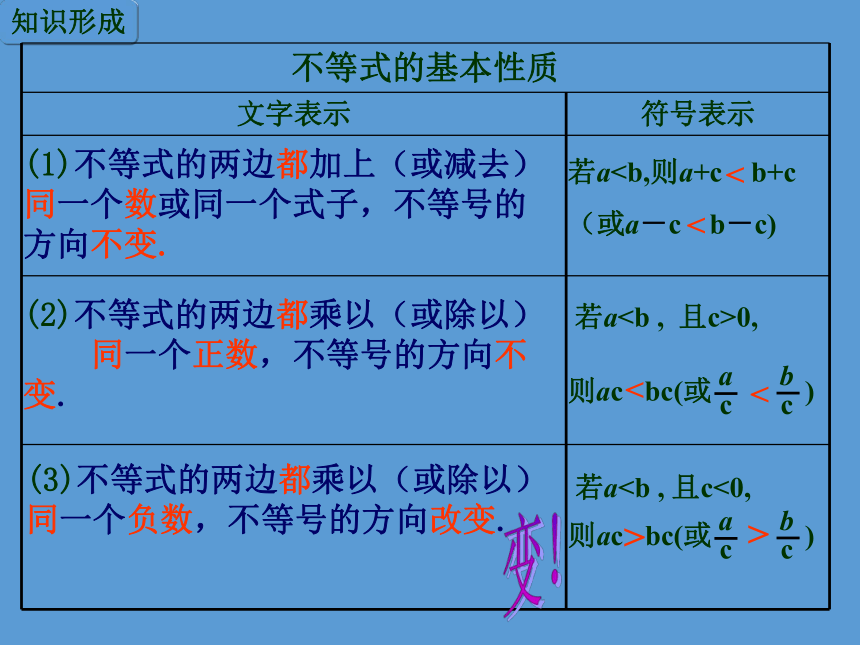
>>><<用“>”或“<”填空 不等式(1) ——(4)分别由不等式“7>4”做了怎样的变形?结果不等号的方向不变还是改变? 再来试一试! -2<6<<>知 识 形 成 不等式(1) ——(4)分别由不等式“-2 <6”做了怎样的变形?结果不等号的方向不变还是改变?知识形成(1)不等式的两边都加上(或减去)同一个数或同一个式子,不等号的方向不变.(2)不等式的两边都乘以(或除以)
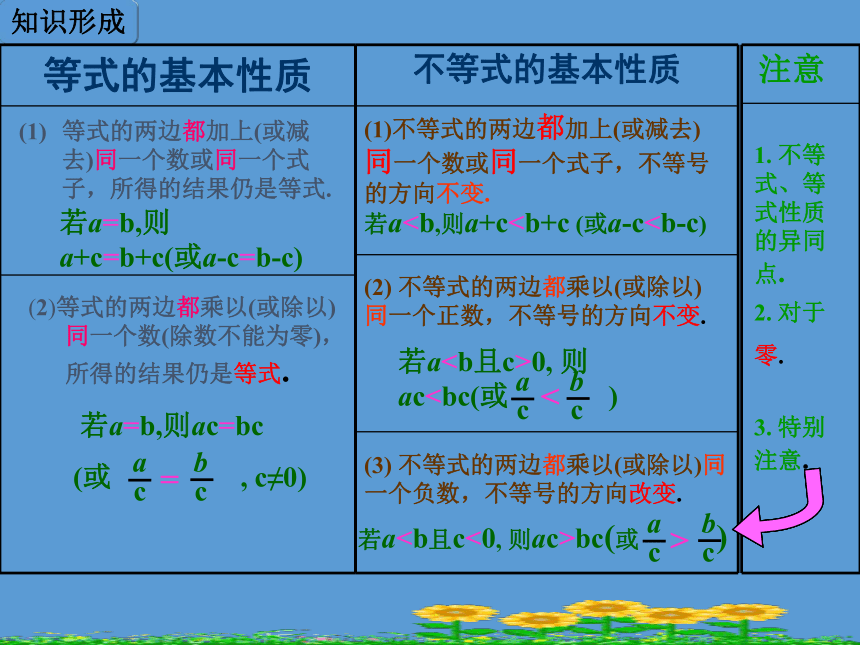
同一个正数,不等号的方向不变.(3)不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.若a(或a-c b-c)<<<<> >变!知识形成(1)不等式的两边都加上(或减去)同一个数或同一个式子,不等号的方向不变.若a0, 则acbc(或 )(3) 不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.等式的两边都加上(或减去)同一个数或同一个式子,所得的结果仍是等式.若a=b,则a+c=b+c(或a-c=b-c) (2)等式的两边都乘以(或除以)同一个数(除数不能为零),所得的结果仍是等式. 若a=b,则ac=bc
(或 , c≠0)1. 不等式、等式性质的异同点.2. 对于
零.3. 特别注意.你认为是这样吗 ?>><例1 解不等式:解:(1)不等式的两边都加上7,不等式的方向不变,x-7+7<8+7,得 x<15(2)不等式的两边都减去2x(即加上-2x),不等号的方向不变,3x-2x<2x-3-2x得 x<-3 这里的变形,与方程变形中的移项相类似,你能说出不等式变形的“移项”该怎么进行吗?(1)x-7<8 (2)3x<2x-3所以所以例2 解不等式:解:(1)不等式的两边都乘以2,不等号的方向不变,得 x>-6得 x>-3所以所以 这里的变形,与方程变形中的“将未知数的系数化为1”相类似,它依据的是不等式的性质2或3,要注意不等式两边乘以(或除以)的数是正数还是负数,确定变形时不等号的方向是否需要改变。 知识应用例3 设a>b,用“<”或“>”填空.
1. a -3____b –3
2. - 4a____ - 4b
3. 2-3a______2-3b><<练习 根据不等式的基本性质,把下列不等式化成
x>a或x(1) x-2<3 (2) 6x<5x-1 (3) x>5 (4) –4x>3(1)解:x-2+2<3+2x<5(2)解:6x-5x<5x-1-5xx<-1(3)解: x×3>5×3x>15(4)解: –4x× <3×x<知识应用判断对错并说明理由1. 因为-3<0,所以-3+1<1 ( ) 2. 因为-3 × 2> -5 ×2,所以-3<-5 ( )7. 因为-2<1,所以-2a < a ( )3. 若ab,则-a<-b ( )6. 若-2x>0,则x>0 ( )8. 若a>0,则3a>2a ( )√√√√××××1.若-m>5,则m _____ - 5.
2.如果x/y>0, 那么xy _____ 0.
3.不等式3x-2<-1解集是 _____ .
4.如果a>-1,那么a-b ____ -1-b.>>x < 1/3<下一页返 回5. 由xmy的条件是 ( )
A . m≥0 B . m≤0 C. m>0 D. m<0
6.若mx1,则应为 ( )
A. m<0 B. m>0 C. m≤0 D. m≥0
7.若m是有理数,则-7m与3m的大小关系应是 ( )
A. -7m<3m B. -7m>3m C. -7m≤3m D. 不能确定DAD看谁做得快8.不等式17-3x>2的正整数解的个数是( )A. 2B. 3C.4D. 5C课 堂 小 结1.不等式的性质是通过与等式的类比、观察、发现、实验、归纳的方法而得到.2.分清不等式、等式性质的异同点.3.注意问题:不等式的基本性质3.练习
解下列不等式,并在数轴上表示出来:
1. x-2>0 2. x+1>0
3. -2x<4 4. 3x≤0
⑵ -2-4____6-4
⑶ -2×4____6×4
⑷ -2÷(-4)___6÷(-4)
>>><<用“>”或“<”填空 不等式(1) ——(4)分别由不等式“7>4”做了怎样的变形?结果不等号的方向不变还是改变? 再来试一试! -2<6<<>知 识 形 成 不等式(1) ——(4)分别由不等式“-2 <6”做了怎样的变形?结果不等号的方向不变还是改变?知识形成(1)不等式的两边都加上(或减去)同一个数或同一个式子,不等号的方向不变.(2)不等式的两边都乘以(或除以)
同一个正数,不等号的方向不变.(3)不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.若a
(或 , c≠0)1. 不等式、等式性质的异同点.2. 对于
零.3. 特别注意.你认为是这样吗 ?>><例1 解不等式:解:(1)不等式的两边都加上7,不等式的方向不变,x-7+7<8+7,得 x<15(2)不等式的两边都减去2x(即加上-2x),不等号的方向不变,3x-2x<2x-3-2x得 x<-3 这里的变形,与方程变形中的移项相类似,你能说出不等式变形的“移项”该怎么进行吗?(1)x-7<8 (2)3x<2x-3所以所以例2 解不等式:解:(1)不等式的两边都乘以2,不等号的方向不变,得 x>-6得 x>-3所以所以 这里的变形,与方程变形中的“将未知数的系数化为1”相类似,它依据的是不等式的性质2或3,要注意不等式两边乘以(或除以)的数是正数还是负数,确定变形时不等号的方向是否需要改变。 知识应用例3 设a>b,用“<”或“>”填空.
1. a -3____b –3
2. - 4a____ - 4b
3. 2-3a______2-3b><<练习 根据不等式的基本性质,把下列不等式化成
x>a或x
2.如果x/y>0, 那么xy _____ 0.
3.不等式3x-2<-1解集是 _____ .
4.如果a>-1,那么a-b ____ -1-b.>>x < 1/3<下一页返 回5. 由x
A . m≥0 B . m≤0 C. m>0 D. m<0
6.若mx
A. m<0 B. m>0 C. m≤0 D. m≥0
7.若m是有理数,则-7m与3m的大小关系应是 ( )
A. -7m<3m B. -7m>3m C. -7m≤3m D. 不能确定DAD看谁做得快8.不等式17-3x>2的正整数解的个数是( )A. 2B. 3C.4D. 5C课 堂 小 结1.不等式的性质是通过与等式的类比、观察、发现、实验、归纳的方法而得到.2.分清不等式、等式性质的异同点.3.注意问题:不等式的基本性质3.练习
解下列不等式,并在数轴上表示出来:
1. x-2>0 2. x+1>0
3. -2x<4 4. 3x≤0
