9.1.1 认识三角形 课件(19张PPT)
文档属性
| 名称 | 9.1.1 认识三角形 课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 183.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 08:41:55 | ||
图片预览




文档简介
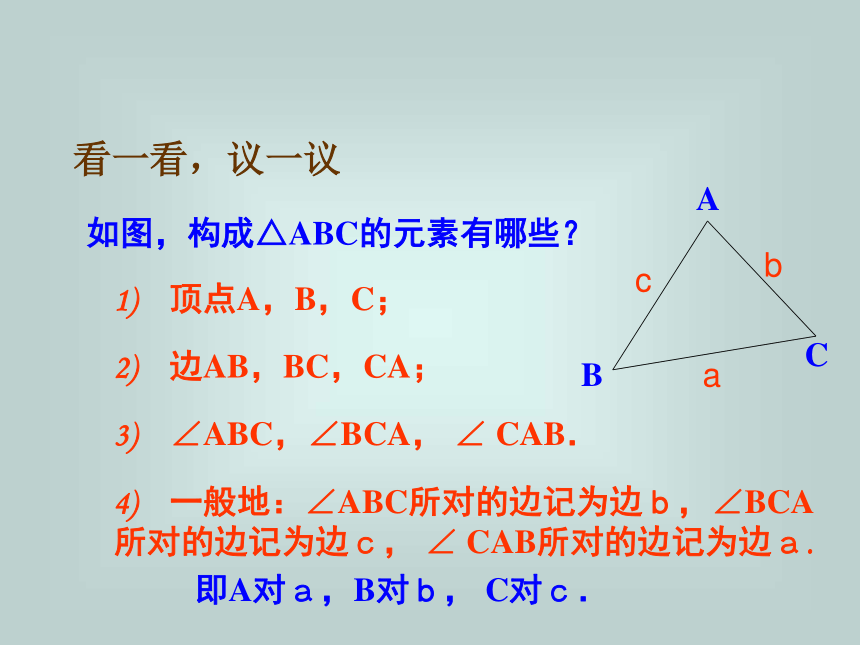
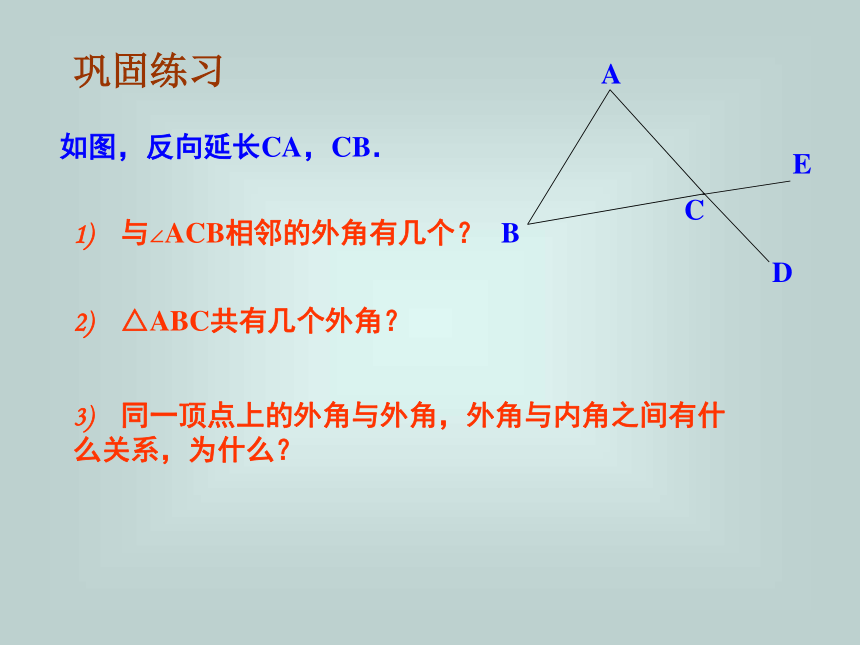
课件19张PPT。认识三角形你能从中找出你熟悉的图形吗?你能举出生活中的三角形吗?生活中的三角形!三条线段首尾顺次连结组成的平面图形。不在同一条直线上的认识三角形看一看,议一议如图,构成△ABC的元素有哪些?1) 顶点A,B,C;2) 边AB,BC,CA;3) ∠ABC,∠BCA, ∠ CAB.4) 一般地:∠ABC所对的边记为边b,∠BCA所对的边记为边c, ∠ CAB所对的边记为边a.即A对a,B对b, C对c.abc三角形的外角D如图,延长△ABC的边BC至D,CD与AC构成了一个新的角——∠ACD.如图,像∠ACD一样,由三角形的一条边和另一条边的反向延长线所组成的角叫三角形的外角.巩固练习如图,反向延长CA,CB.1) 与∠ACB相邻的外角有几个?2) △ABC共有几个外角?3) 同一顶点上的外角与外角,外角与内角之间有什么关系,为什么?梳理概括顶点边内角外角三 角 形 的 构 成例、图中以BC为边的三角形共有______个;它们分别______________________________.4△BCF; △ BCE; △ BCD; △ BCA图中,三个三角形的内角各有什么特点?第一个三角形中,三个内角均为锐角;第二个三角形中,有一个内角是直角;第三个三角形中,有一个内角是钝角.三角形可以按角来分类:
所有内角都是锐角――锐角三角形;
有一个内角是直角――直角三角形;
有一个内角是钝角――钝角三角形;观察这三个三角形的边各有什么特点?第一个三角形的三边互不相等;第二个三角形有两条边相等;第三个三角形的三边都相等.我们把两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰;把三条边都相等的三角形称为等边三角形(或正三角形).梳理概括一般三角形 等腰三角形 有两边相等 相等的两边与另一边相等 等边三角形 综合练习:判断对错,并说出理由:
(1)锐角三角形中最大的角一定小于90度。 ( )
(2)所有的等边三角形都是等腰三角形。 ( )
(3)所有的等腰三角形都是锐角三角形。 ( )
(4)等腰三角形有两个角是相等的。 ( )
(5)三个角都相等的三角形一定是等边三角形。( )
(6)直角三角形一定不是等腰三角形。 ( )
√
×√√×√ 判断满足下列条件的△ABC是锐角三角形、直角三角形还是钝角三角形?
(1)∠A=90°-∠B;
(2)∠A=∠B= ∠C;
(3)∠A=36°,∠B=2∠C.议一议一个三角形中能不能有两个直角
或两个钝角?会不会有一个平角?如图,说出图中有多少个三角形,用符号“△”表示,并指出每个三角形的三条边.∠G是哪几个三角形的内角?∠FEH的外角是哪一个?(1)图中,共有__个三角形,它们是_________.
(2)△ADC的三个顶点是____.三个内角是______.
(3)AC是哪些三角形的边?_________.
(4)∠AED是____和_____的内角,又是____的外角.钝角三角形直角三角形课 堂 小 结1.什么是三角形?2.有关三角形的构成.顶点边内角外角 由不在同一直线上的三条线段首尾顺次连结而成的平面图形,叫三角形.(一条边和另一条边的反向延长线)3. 三角形的分类.
所有内角都是锐角――锐角三角形;
有一个内角是直角――直角三角形;
有一个内角是钝角――钝角三角形;观察这三个三角形的边各有什么特点?第一个三角形的三边互不相等;第二个三角形有两条边相等;第三个三角形的三边都相等.我们把两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰;把三条边都相等的三角形称为等边三角形(或正三角形).梳理概括一般三角形 等腰三角形 有两边相等 相等的两边与另一边相等 等边三角形 综合练习:判断对错,并说出理由:
(1)锐角三角形中最大的角一定小于90度。 ( )
(2)所有的等边三角形都是等腰三角形。 ( )
(3)所有的等腰三角形都是锐角三角形。 ( )
(4)等腰三角形有两个角是相等的。 ( )
(5)三个角都相等的三角形一定是等边三角形。( )
(6)直角三角形一定不是等腰三角形。 ( )
√
×√√×√ 判断满足下列条件的△ABC是锐角三角形、直角三角形还是钝角三角形?
(1)∠A=90°-∠B;
(2)∠A=∠B= ∠C;
(3)∠A=36°,∠B=2∠C.议一议一个三角形中能不能有两个直角
或两个钝角?会不会有一个平角?如图,说出图中有多少个三角形,用符号“△”表示,并指出每个三角形的三条边.∠G是哪几个三角形的内角?∠FEH的外角是哪一个?(1)图中,共有__个三角形,它们是_________.
(2)△ADC的三个顶点是____.三个内角是______.
(3)AC是哪些三角形的边?_________.
(4)∠AED是____和_____的内角,又是____的外角.钝角三角形直角三角形课 堂 小 结1.什么是三角形?2.有关三角形的构成.顶点边内角外角 由不在同一直线上的三条线段首尾顺次连结而成的平面图形,叫三角形.(一条边和另一条边的反向延长线)3. 三角形的分类.
