8.1 认识不等式 教学设计(表格式)
文档属性
| 名称 | 8.1 认识不等式 教学设计(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 37.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 08:41:55 | ||
图片预览

文档简介
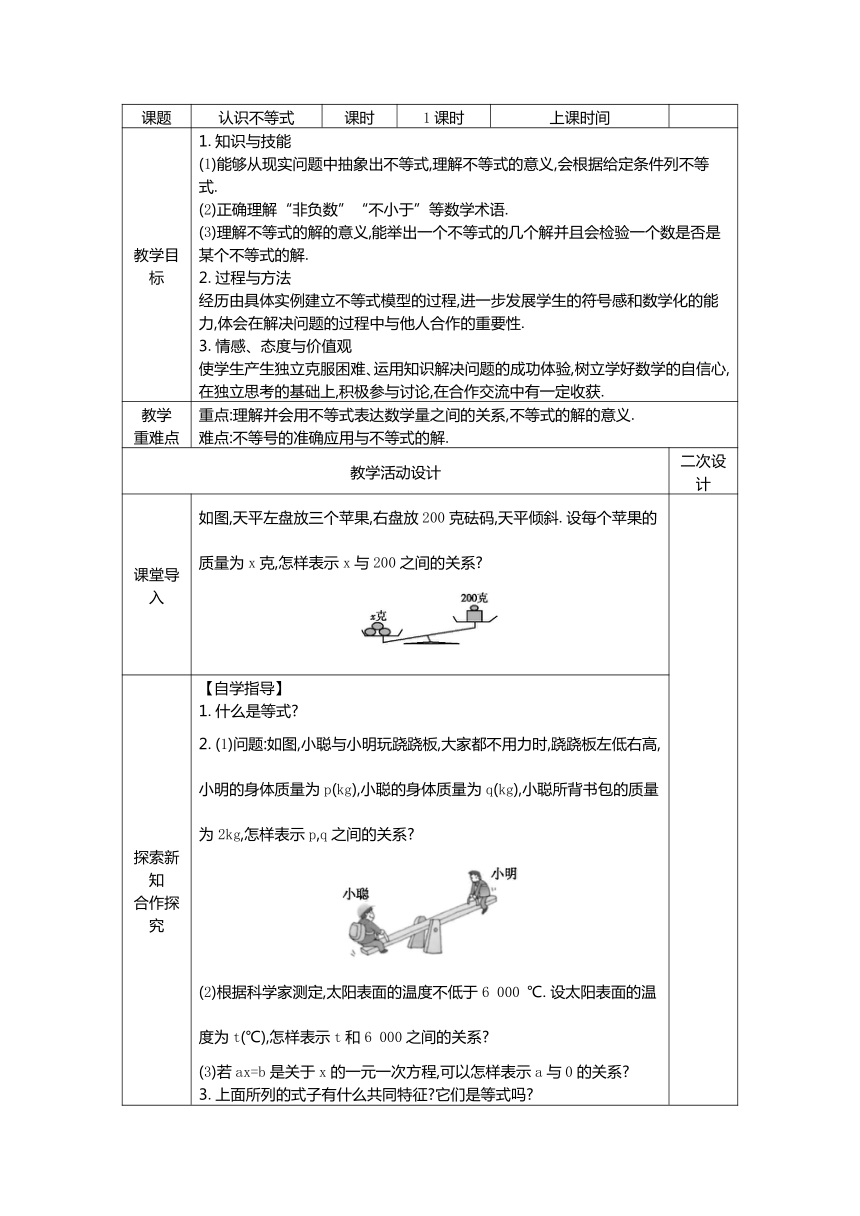
课题
认识不等式
课时
1课时
上课时间
教学目标
1.知识与技能
(1)能够从现实问题中抽象出不等式,理解不等式的意义,会根据给定条件列不等式.
(2)正确理解“非负数”“不小于”等数学术语.
(3)理解不等式的解的意义,能举出一个不等式的几个解并且会检验一个数是否是某个不等式的解.
2.过程与方法
经历由具体实例建立不等式模型的过程,进一步发展学生的符号感和数学化的能力,体会在解决问题的过程中与他人合作的重要性.
3.情感、态度与价值观
使学生产生独立克服困难、运用知识解决问题的成功体验,树立学好数学的自信心,在独立思考的基础上,积极参与讨论,在合作交流中有一定收获.
教学
重难点
重点:理解并会用不等式表达数学量之间的关系,不等式的解的意义.
难点:不等号的准确应用与不等式的解.
教学活动设计
二次设计
课堂导入
如图,天平左盘放三个苹果,右盘放200克砝码,天平倾斜.设每个苹果的质量为x克,怎样表示x与200之间的关系?
探索新知
合作探究
【自学指导】
1.什么是等式?
2.(1)问题:如图,小聪与小明玩跷跷板,大家都不用力时,跷跷板左低右高,小明的身体质量为p(kg),小聪的身体质量为q(kg),小聪所背书包的质量为2kg,怎样表示p,q之间的关系?
(2)根据科学家测定,太阳表面的温度不低于6 000 ℃.设太阳表面的温度为t(℃),怎样表示t和6 000之间的关系?
(3)若ax=b是关于x的一元一次方程,可以怎样表示a与0的关系?
3.上面所列的式子有什么共同特征?它们是等式吗?
4.自学课本P50~51,说出不等式的概念,并举出几个不等式的例子.
【合作探究】
1.小组讨论自学指导中出现疑问的地方.
2.小组讨论什么样的式子是不等式?常见的不等号有哪些?教师进行补充,总结.
3.小组讨论交流什么是不等式的解?怎样确定不等式的解?
续表
探索新知
合作探究
【教师指导】
一、易错点:
1.混淆不等式与代数式.
2.用不等式表示不等关系时应用不等号错误.
3.不能从实际问题中抽象出不等关系.
二、归纳小结:
1.不等式的概念:用不等号表示不等关系的式子.
2.不等式的解:能使不等式成立的未知数的值.
三、方法规律:根据实际问题列不等式
1.分析题意,找出各个量,并用代数式表示.
2.找出表示不等关系的词语,如“大,小,多,少,超过,至多,至少,不少于,不多于”等.
3.将不等关系用不等号表示出来.
当堂训练
1.下列不等式中,正确的是( )
(A)m与4的差是负数,可表示为m-4<0
(B)x不大于3可表示为x<3
(C)a是非正数可表示为a<0
(D)x与2的和是非负数可表示为x+2>0
2.给出下面5个式子:①3>0;②4x+3y≠0;③x=3;④x-1;⑤x+2≤3,其中不等式有 个.?
3.对于不等式2x>6,x=2,x=3,x=4,x=5,哪些是2x>6的解?哪些不是?
4.某市自来水公司按如下标准收取水费:若每户每月用水不超过10 m3,则每立方米收费1.5元;若每户每月用水超过10 m3,则超过的部分每立方米收费2元.小亮家某月的水费不少于25元,那么他家该月的用水量x(m3)至少是多少?请列出关于x的不等式.
板书设计
认识不等式
1.不等式的概念
2.不等式的解
3.列不等式
教学反思
认识不等式
课时
1课时
上课时间
教学目标
1.知识与技能
(1)能够从现实问题中抽象出不等式,理解不等式的意义,会根据给定条件列不等式.
(2)正确理解“非负数”“不小于”等数学术语.
(3)理解不等式的解的意义,能举出一个不等式的几个解并且会检验一个数是否是某个不等式的解.
2.过程与方法
经历由具体实例建立不等式模型的过程,进一步发展学生的符号感和数学化的能力,体会在解决问题的过程中与他人合作的重要性.
3.情感、态度与价值观
使学生产生独立克服困难、运用知识解决问题的成功体验,树立学好数学的自信心,在独立思考的基础上,积极参与讨论,在合作交流中有一定收获.
教学
重难点
重点:理解并会用不等式表达数学量之间的关系,不等式的解的意义.
难点:不等号的准确应用与不等式的解.
教学活动设计
二次设计
课堂导入
如图,天平左盘放三个苹果,右盘放200克砝码,天平倾斜.设每个苹果的质量为x克,怎样表示x与200之间的关系?
探索新知
合作探究
【自学指导】
1.什么是等式?
2.(1)问题:如图,小聪与小明玩跷跷板,大家都不用力时,跷跷板左低右高,小明的身体质量为p(kg),小聪的身体质量为q(kg),小聪所背书包的质量为2kg,怎样表示p,q之间的关系?
(2)根据科学家测定,太阳表面的温度不低于6 000 ℃.设太阳表面的温度为t(℃),怎样表示t和6 000之间的关系?
(3)若ax=b是关于x的一元一次方程,可以怎样表示a与0的关系?
3.上面所列的式子有什么共同特征?它们是等式吗?
4.自学课本P50~51,说出不等式的概念,并举出几个不等式的例子.
【合作探究】
1.小组讨论自学指导中出现疑问的地方.
2.小组讨论什么样的式子是不等式?常见的不等号有哪些?教师进行补充,总结.
3.小组讨论交流什么是不等式的解?怎样确定不等式的解?
续表
探索新知
合作探究
【教师指导】
一、易错点:
1.混淆不等式与代数式.
2.用不等式表示不等关系时应用不等号错误.
3.不能从实际问题中抽象出不等关系.
二、归纳小结:
1.不等式的概念:用不等号表示不等关系的式子.
2.不等式的解:能使不等式成立的未知数的值.
三、方法规律:根据实际问题列不等式
1.分析题意,找出各个量,并用代数式表示.
2.找出表示不等关系的词语,如“大,小,多,少,超过,至多,至少,不少于,不多于”等.
3.将不等关系用不等号表示出来.
当堂训练
1.下列不等式中,正确的是( )
(A)m与4的差是负数,可表示为m-4<0
(B)x不大于3可表示为x<3
(C)a是非正数可表示为a<0
(D)x与2的和是非负数可表示为x+2>0
2.给出下面5个式子:①3>0;②4x+3y≠0;③x=3;④x-1;⑤x+2≤3,其中不等式有 个.?
3.对于不等式2x>6,x=2,x=3,x=4,x=5,哪些是2x>6的解?哪些不是?
4.某市自来水公司按如下标准收取水费:若每户每月用水不超过10 m3,则每立方米收费1.5元;若每户每月用水超过10 m3,则超过的部分每立方米收费2元.小亮家某月的水费不少于25元,那么他家该月的用水量x(m3)至少是多少?请列出关于x的不等式.
板书设计
认识不等式
1.不等式的概念
2.不等式的解
3.列不等式
教学反思
