2020版高中数学新人教B版选修1-1第三章导数及其应用3.1.3导数的几何意义课件(43张PPT)
文档属性
| 名称 | 2020版高中数学新人教B版选修1-1第三章导数及其应用3.1.3导数的几何意义课件(43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-29 18:12:15 | ||
图片预览











文档简介
课件43张PPT。3.1.3 导数的几何意义第三章 §3.1 导 数学习目标XUEXIMUBIAO1.了解导函数的概念,理解导数的几何意义.
2.会求简单函数的导函数.
3.根据导数的几何意义,会求曲线上某点处的切线方程.
4.正确理解曲线“过某点”和“在某点”处的切线,并会求其方程.NEIRONGSUOYIN内容索引自主学习题型探究达标检测1自主学习PART ONE知识点 导数的几何意义
(1)切线的概念:如图,对于割线PPn,当点Pn趋近于点P时,割线PPn趋近于确定的位置,这个确定位置的 称为点P处的切线.直线PT(2)导数的几何意义:函数f(x)在x=x0处的导数就是切线PT的斜率k,即k=
=f′(x0).
(3)切线方程:
曲线y=f(x)在点(x0,f(x0))处的切线方程为 .
特别提醒:曲线的切线并不一定与曲线只有一个交点,可能有多个,甚至可以无穷多.与曲线只有一个公共点的直线也不一定是曲线的切线.y-f(x0)=f′(x0)(x-x0)1.过曲线上一点的割线有无数条,而过这点的切线却仅有一条.( )
2.曲线在点P处的切线和过点P的切线意思相同.( )
3.这里对曲线切线的定义与圆的切线的定义并不完全相同.( )思考辨析 判断正误SIKAOBIANXIPANDUANZHENGWU√××2题型探究PART TWO题型一 求切线方程命题角度1 曲线在某点处的切线方程
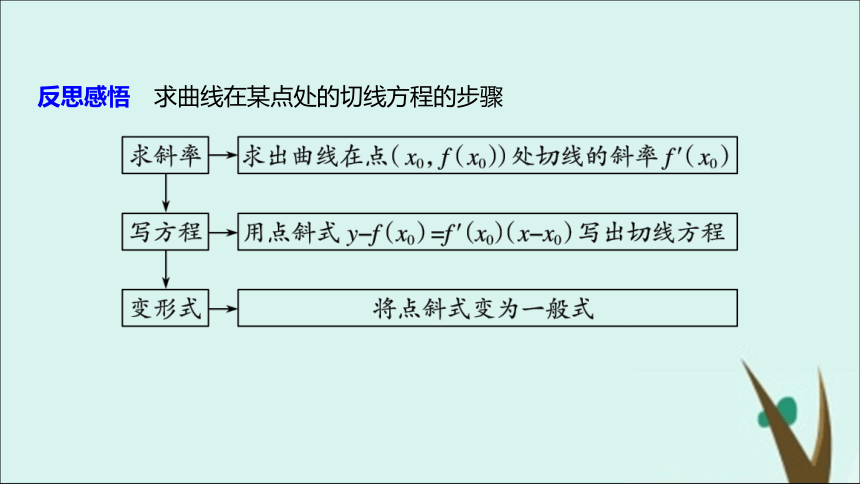
例1 已知曲线C: ,求曲线C在横坐标为2的点处的切线方程.多维探究解 将x=2代入曲线C的方程得y=4,
∴切点坐标为P(2,4).∴k=y′|x=2=4.
∴曲线在点P(2,4)处的切线方程为
y-4=4(x-2),即4x-y-4=0.反思感悟 求曲线在某点处的切线方程的步骤∴k=y′|x=2=4.
∴曲线y=x2+1在点(2,5)处的切线方程为
y-5=4(x-2),即y=4x-3.
∴切线与y轴交点的纵坐标是-3.跟踪训练1 曲线y=x2+1在点P(2,5)处的切线与y轴交点的纵坐标是____.-3命题角度2 曲线过某点的切线方程即x-8x0+7=0,解得x0=7或x0=1.化简得14x-4y-49=0或2x-4y-1=0,
即为所求的切线方程.反思感悟 过点(x1,y1)的曲线y=f(x)的切线方程的求法步骤
(1)设切点(x0,y0).
(3)解方程k=f′(x0),得x0,y0,从而写出切线方程.跟踪训练2 求过点(-1,0)与曲线y=x2+x+1相切的直线方程.解得x0=0或x0=-2.
当x0=0时,切线的斜率为k=1,过(-1,0)的切线方程为y-0=x+1,
即x-y+1=0;当x0=-2时,切线的斜率为k=-3,
过(-1,0)的切线方程为y-0=-3(x+1),即3x+y+3=0.
故所求切线方程为x-y+1=0或3x+y+3=0.题型二 求切点坐标例3 已知曲线y1=x2-1在x=x0处的切线与曲线y2=1-x3在x=x0处的切线互相平行,求x0的值.引申探究
1.若将本例条件中的“平行”改为“垂直”,求x0的值.又曲线y1=x2-1与y2=1-x3在x=x0处的切线互相垂直,2.若本例条件不变,试求出两条平行的切线方程.当x0=0时,两条平行切线方程分别为y=-1,y=1.曲线y=1-x3的切线方程为36x+27y-11=0.
∴所求两平行切线方程为y=-1与y=1或12x+9y+13=0与36x+27y-11=0.反思感悟 根据切线斜率求切点坐标的步骤
(1)设切点坐标(x0,y0).
(2)求导函数f′(x).
(3)求切线的斜率f′(x0).
(4)由斜率间的关系列出关于x0的方程,解方程求x0.
(5)点(x0,y0)在曲线f(x)上,将x0代入求y0,得切点坐标.跟踪训练3 已知直线l:y=4x+a与曲线C:y=x3-2x2+3相切,求a的值及切点坐标.解 设直线l与曲线C相切于点P(x0,y0).当切点坐标为(2,3)时,有3=4×2+a,解得a=-5.当a=-5时,切点坐标为(2,3).题型三 导数几何意义的应用例4 (1)函数g(x)的图象如图所示,下列数值排序正确的是
A.0B.0C.0D.0当x≥0时,g′(x)>0且曲线的切线的斜率逐渐增大,
∴g′(x)单调递增,∴g′(2)∵g(x)上升的越来越快,∴g′(2)∴0将x=2,y=8+a代入到8x-y-15=0中,
得a=-7.反思感悟 利用导数的几何意义将数与形联系起来,根据图象中切线与割线的倾斜角的大小确定数据的大小.A.f′(1)B.f′(1)C.f′(2)D.a由点斜式得切线方程为y-a3=3a2(x-a).解得a=±1.令x=a,得y=a3,核心素养之直观想象HEXINSUYANGZHIZHIGUANXIANGXIANG求切线倾斜角的范围解 设P(x0,y0),设直线l的倾斜角为α(0≤α<π),
∴tan α≥-1,素养评析 (1)某点处的导数就是该点处切线的倾斜角的正切值,倾斜角范围的确定需利用正切函数图象,借助于图象易于求得倾斜角的范围.
(2)建立形与数的联系,借助于几何直观理解问题,有利于提升学生的数形结合能力,形成数学直观直觉.3达标检测PART THREE1.如果一个函数的瞬时变化率处处为0,则这个函数的图象是
A.半圆 B.抛物线 C.双曲线 D.直线1234√解析 由题意,函数是常数函数y=c(c为常数).512342.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则
A.a=1,b=1 B.a=-1,b=1
C.a=1,b=-1 D.a=-1,b=-1√解析 由题意知,k=y′|x=0∴a=1.又(0,b)在切线上,∴b=1,故选A.53.曲线y=f(x)= 在点(3,3)处的切线的倾斜角等于
A.45° B.60° C.135° D.120°√1234又∵直线倾斜角的范围为[0°,180°),
∴倾斜角为135°.512344.如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则函数f(x)在x=1处的导数f′(1)=____.-2由导数的几何意义,知f(x)在x=1处的斜率为-2.512345.已知曲线y=f(x)=2x2+4x在点P处的切线斜率为16,则点P的坐标为________.(3,30)令4x0+4=16,得x0=3,∴P(3,30).5课堂小结KETANGXIAOJIE2.“函数f(x)在点x0处的导数”是一个常数,不是变量,“导函数”是一个函数,二者有本质的区别,但又有密切关系,f′(x0)是其导数y=f′(x)在x=x0处的一个函数值.
3.利用导数求曲线的切线方程,要注意已知点是否在曲线上.如果已知点在曲线上,则以该点为切点的切线方程为y-f(x0)=f′(x0)(x-x0);若已知点不在切线上,则应先设出切点(x0,f(x0)),表示出切线方程,然后求出切点.
2.会求简单函数的导函数.
3.根据导数的几何意义,会求曲线上某点处的切线方程.
4.正确理解曲线“过某点”和“在某点”处的切线,并会求其方程.NEIRONGSUOYIN内容索引自主学习题型探究达标检测1自主学习PART ONE知识点 导数的几何意义
(1)切线的概念:如图,对于割线PPn,当点Pn趋近于点P时,割线PPn趋近于确定的位置,这个确定位置的 称为点P处的切线.直线PT(2)导数的几何意义:函数f(x)在x=x0处的导数就是切线PT的斜率k,即k=
=f′(x0).
(3)切线方程:
曲线y=f(x)在点(x0,f(x0))处的切线方程为 .
特别提醒:曲线的切线并不一定与曲线只有一个交点,可能有多个,甚至可以无穷多.与曲线只有一个公共点的直线也不一定是曲线的切线.y-f(x0)=f′(x0)(x-x0)1.过曲线上一点的割线有无数条,而过这点的切线却仅有一条.( )
2.曲线在点P处的切线和过点P的切线意思相同.( )
3.这里对曲线切线的定义与圆的切线的定义并不完全相同.( )思考辨析 判断正误SIKAOBIANXIPANDUANZHENGWU√××2题型探究PART TWO题型一 求切线方程命题角度1 曲线在某点处的切线方程
例1 已知曲线C: ,求曲线C在横坐标为2的点处的切线方程.多维探究解 将x=2代入曲线C的方程得y=4,
∴切点坐标为P(2,4).∴k=y′|x=2=4.
∴曲线在点P(2,4)处的切线方程为
y-4=4(x-2),即4x-y-4=0.反思感悟 求曲线在某点处的切线方程的步骤∴k=y′|x=2=4.
∴曲线y=x2+1在点(2,5)处的切线方程为
y-5=4(x-2),即y=4x-3.
∴切线与y轴交点的纵坐标是-3.跟踪训练1 曲线y=x2+1在点P(2,5)处的切线与y轴交点的纵坐标是____.-3命题角度2 曲线过某点的切线方程即x-8x0+7=0,解得x0=7或x0=1.化简得14x-4y-49=0或2x-4y-1=0,
即为所求的切线方程.反思感悟 过点(x1,y1)的曲线y=f(x)的切线方程的求法步骤
(1)设切点(x0,y0).
(3)解方程k=f′(x0),得x0,y0,从而写出切线方程.跟踪训练2 求过点(-1,0)与曲线y=x2+x+1相切的直线方程.解得x0=0或x0=-2.
当x0=0时,切线的斜率为k=1,过(-1,0)的切线方程为y-0=x+1,
即x-y+1=0;当x0=-2时,切线的斜率为k=-3,
过(-1,0)的切线方程为y-0=-3(x+1),即3x+y+3=0.
故所求切线方程为x-y+1=0或3x+y+3=0.题型二 求切点坐标例3 已知曲线y1=x2-1在x=x0处的切线与曲线y2=1-x3在x=x0处的切线互相平行,求x0的值.引申探究
1.若将本例条件中的“平行”改为“垂直”,求x0的值.又曲线y1=x2-1与y2=1-x3在x=x0处的切线互相垂直,2.若本例条件不变,试求出两条平行的切线方程.当x0=0时,两条平行切线方程分别为y=-1,y=1.曲线y=1-x3的切线方程为36x+27y-11=0.
∴所求两平行切线方程为y=-1与y=1或12x+9y+13=0与36x+27y-11=0.反思感悟 根据切线斜率求切点坐标的步骤
(1)设切点坐标(x0,y0).
(2)求导函数f′(x).
(3)求切线的斜率f′(x0).
(4)由斜率间的关系列出关于x0的方程,解方程求x0.
(5)点(x0,y0)在曲线f(x)上,将x0代入求y0,得切点坐标.跟踪训练3 已知直线l:y=4x+a与曲线C:y=x3-2x2+3相切,求a的值及切点坐标.解 设直线l与曲线C相切于点P(x0,y0).当切点坐标为(2,3)时,有3=4×2+a,解得a=-5.当a=-5时,切点坐标为(2,3).题型三 导数几何意义的应用例4 (1)函数g(x)的图象如图所示,下列数值排序正确的是
A.0
∴g′(x)单调递增,∴g′(2)
得a=-7.反思感悟 利用导数的几何意义将数与形联系起来,根据图象中切线与割线的倾斜角的大小确定数据的大小.A.f′(1)
∴tan α≥-1,素养评析 (1)某点处的导数就是该点处切线的倾斜角的正切值,倾斜角范围的确定需利用正切函数图象,借助于图象易于求得倾斜角的范围.
(2)建立形与数的联系,借助于几何直观理解问题,有利于提升学生的数形结合能力,形成数学直观直觉.3达标检测PART THREE1.如果一个函数的瞬时变化率处处为0,则这个函数的图象是
A.半圆 B.抛物线 C.双曲线 D.直线1234√解析 由题意,函数是常数函数y=c(c为常数).512342.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则
A.a=1,b=1 B.a=-1,b=1
C.a=1,b=-1 D.a=-1,b=-1√解析 由题意知,k=y′|x=0∴a=1.又(0,b)在切线上,∴b=1,故选A.53.曲线y=f(x)= 在点(3,3)处的切线的倾斜角等于
A.45° B.60° C.135° D.120°√1234又∵直线倾斜角的范围为[0°,180°),
∴倾斜角为135°.512344.如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则函数f(x)在x=1处的导数f′(1)=____.-2由导数的几何意义,知f(x)在x=1处的斜率为-2.512345.已知曲线y=f(x)=2x2+4x在点P处的切线斜率为16,则点P的坐标为________.(3,30)令4x0+4=16,得x0=3,∴P(3,30).5课堂小结KETANGXIAOJIE2.“函数f(x)在点x0处的导数”是一个常数,不是变量,“导函数”是一个函数,二者有本质的区别,但又有密切关系,f′(x0)是其导数y=f′(x)在x=x0处的一个函数值.
3.利用导数求曲线的切线方程,要注意已知点是否在曲线上.如果已知点在曲线上,则以该点为切点的切线方程为y-f(x0)=f′(x0)(x-x0);若已知点不在切线上,则应先设出切点(x0,f(x0)),表示出切线方程,然后求出切点.
