2020版高中数学新人教B版选修1-1第三章导数及其应用3.2.1常数与幂函数的导数3.2.2导数公式表课件(30张PPT)
文档属性
| 名称 | 2020版高中数学新人教B版选修1-1第三章导数及其应用3.2.1常数与幂函数的导数3.2.2导数公式表课件(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-29 18:12:48 | ||
图片预览











文档简介
课件30张PPT。3.2.1 常数与幂函数的导数
3.2.2 导数公式表第三章 §3.2 导数的运算学习目标XUEXIMUBIAO1.能根据定义求函数y=C,y=x,y=x2,y= 的导数.
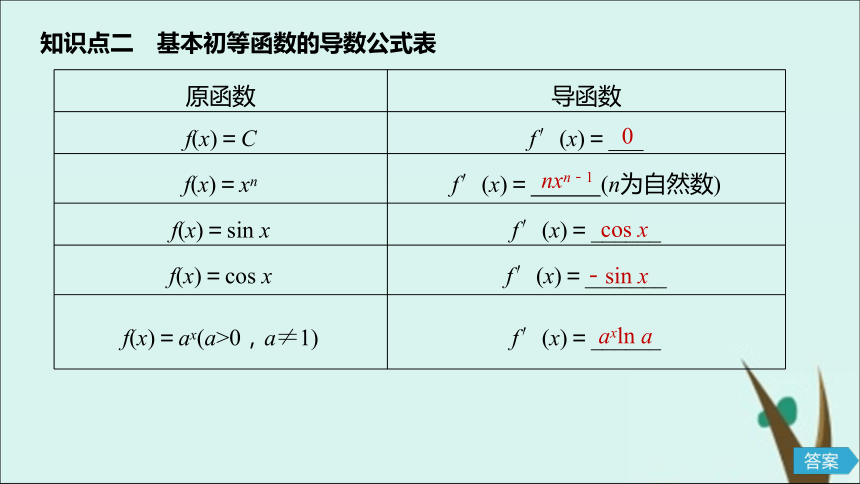
2.能利用给出的基本初等函数的导数公式求简单函数的导数.NEIRONGSUOYIN内容索引自主学习题型探究达标检测1自主学习PART ONE知识点一 常数与幂函数的导数012x知识点二 基本初等函数的导数公式表0nxn-1cos x-sin xaxln aex 2题型探究PART TWO题型一 利用导数公式求函数的导数例1 求下列函数的导数.
(1)y=x12;解 y′=(x12)′=12x12-1=12x11.(6)y=3x.解 y′=(3x)′=3xln 3.反思感悟 若题目中所给出的函数解析式不适用导数公式,需通过恒等变换对解析式进行化简或变形后求导,如根式化成指数幂的形式求导.跟踪训练1 求下列函数的导数.
(1)y=lg x;∴y′=(cos x)′=-sin x.题型二 导数公式的综合应用命题角度1 利用导数公式解决切线问题
例2 已知点P(-1,1),点Q(2,4)是曲线y=x2上两点,是否存在与直线PQ垂直的切线,若有,求出切线方程,若没有,说明理由.多维探究解 因为y′=(x2)′=2x,假设存在与直线PQ垂直的切线.即4x+4y+1=0.引申探究
若本例条件不变,求与直线PQ平行的曲线y=x2的切线方程.解 因为y′=(x2)′=2x,设切点为M(x0,y0),
则 =2x0.反思感悟 解决切线问题,关键是确定切点,要充分利用:
(1)切点处的导数是切线的斜率.
(2)切点在切线上.
(3)切点又在曲线上这三个条件联立方程解决.跟踪训练2 已知两条曲线y=sin x,y=cos x,是否存在这两条曲线的一个公共点,使在这一点处两条曲线的切线互相垂直?并说明理由.解 设存在一个公共点(x0,y0),使两曲线的切线垂直,
则在点(x0,y0)处的切线斜率分别为k1= =cos x0,k2= =-sin x0.
要使两切线垂直,必须有k1k2=cos x0(-sin x0)=-1,
即sin 2x0=2,这是不可能的.
所以两条曲线不存在公共点,使在这一点处两条曲线的切线互相垂直.命题角度2 利用导数公式解决最值问题
例3 求抛物线y=x2上的点到直线x-y-2=0的最短距离.反思感悟 利用基本初等函数的求导公式,可求其图象在某一点P(x0,y0)处的切线方程,可以解决一些与距离、面积相关的几何的最值问题,一般都与函数图象的切线有关.解题时可先利用图象分析取最值时的位置情况,再利用导数的几何意义准确计算.跟踪训练3 已知直线l: 2x-y+4=0与抛物线y=x2相交于A,B两点,O是坐标原点,试求与直线l平行的抛物线的切线方程,并在弧 上求一点P,使△ABP的面积最大.解 设M(x0,y0)为切点,过点M与直线l平行的直线斜率为k=y′=2x0,
∴k=2x0=2,∴x0=1,y0 =1,故可得M(1,1),
∴切线方程为2x-y-1=0.
由于直线l: 2x-y+4=0与抛物线y=x2相交于A,B两点,
∴|AB|为定值,要使△ABP的面积最大,只要P到AB的距离最大,
故点M(1,1)即为所求弧 上的点,使△ABP的面积最大.核心素养之数学运算HEXINSUYANGZHISHUXUEYUNSUAN导数公式的应用典例 设f0(x)=sin x,f1(x)=f′0(x),f2(x)=f′1(x),…,fn+1(x)=f′n(x),n∈N,则f2 019(x)等于
A.sin x B.-sin x
C.cos x D.-cos x√解析 f1(x)=f′0(x)=(sin x)′=cos x,
f2(x)=f′1(x)=(cos x)′=-sin x,
f3(x)=f′2(x)=(-sin x)′=-cos x,
f4(x)=(-cos x)′=sin x,
f5(x)=(sin x)′=f1(x),
f6(x)=f2(x),…,
fn+4(x)=fn(x),
可知fn(x)关于n的周期为4,
∴f2 019(x)=f504×4+3(x)=-cos x.素养评析 熟记导数公式是进行导数运算的前提,正确的进行导数运算,方能找出规律,寻找到正确的结论.3达标检测PART THREE1.下列结论:
①(sin x)′=cos x;② ;
③(log3x)′= ;④(ln x)′= .
其中正确的有
A.0个 B.1个 C.2个 D.3个1234√∴②③错误,故选C.1234√3.设函数f(x)=logax,f′(1)=-1,则a=___.12342344.求过曲线y=sin x上的点 且与在这一点处的切线垂直的直线方程.1课堂小结KETANGXIAOJIE1.利用常见函数的导数公式可以比较简便地求出函数的导数,其关键是牢记和运用好导数公式.解题时,能认真观察函数的结构特征,积极地进行联想化归.3.对于正弦、余弦函数的导数,一是注意函数名称的变化,二是注意函数符号的变化.
3.2.2 导数公式表第三章 §3.2 导数的运算学习目标XUEXIMUBIAO1.能根据定义求函数y=C,y=x,y=x2,y= 的导数.
2.能利用给出的基本初等函数的导数公式求简单函数的导数.NEIRONGSUOYIN内容索引自主学习题型探究达标检测1自主学习PART ONE知识点一 常数与幂函数的导数012x知识点二 基本初等函数的导数公式表0nxn-1cos x-sin xaxln aex 2题型探究PART TWO题型一 利用导数公式求函数的导数例1 求下列函数的导数.
(1)y=x12;解 y′=(x12)′=12x12-1=12x11.(6)y=3x.解 y′=(3x)′=3xln 3.反思感悟 若题目中所给出的函数解析式不适用导数公式,需通过恒等变换对解析式进行化简或变形后求导,如根式化成指数幂的形式求导.跟踪训练1 求下列函数的导数.
(1)y=lg x;∴y′=(cos x)′=-sin x.题型二 导数公式的综合应用命题角度1 利用导数公式解决切线问题
例2 已知点P(-1,1),点Q(2,4)是曲线y=x2上两点,是否存在与直线PQ垂直的切线,若有,求出切线方程,若没有,说明理由.多维探究解 因为y′=(x2)′=2x,假设存在与直线PQ垂直的切线.即4x+4y+1=0.引申探究
若本例条件不变,求与直线PQ平行的曲线y=x2的切线方程.解 因为y′=(x2)′=2x,设切点为M(x0,y0),
则 =2x0.反思感悟 解决切线问题,关键是确定切点,要充分利用:
(1)切点处的导数是切线的斜率.
(2)切点在切线上.
(3)切点又在曲线上这三个条件联立方程解决.跟踪训练2 已知两条曲线y=sin x,y=cos x,是否存在这两条曲线的一个公共点,使在这一点处两条曲线的切线互相垂直?并说明理由.解 设存在一个公共点(x0,y0),使两曲线的切线垂直,
则在点(x0,y0)处的切线斜率分别为k1= =cos x0,k2= =-sin x0.
要使两切线垂直,必须有k1k2=cos x0(-sin x0)=-1,
即sin 2x0=2,这是不可能的.
所以两条曲线不存在公共点,使在这一点处两条曲线的切线互相垂直.命题角度2 利用导数公式解决最值问题
例3 求抛物线y=x2上的点到直线x-y-2=0的最短距离.反思感悟 利用基本初等函数的求导公式,可求其图象在某一点P(x0,y0)处的切线方程,可以解决一些与距离、面积相关的几何的最值问题,一般都与函数图象的切线有关.解题时可先利用图象分析取最值时的位置情况,再利用导数的几何意义准确计算.跟踪训练3 已知直线l: 2x-y+4=0与抛物线y=x2相交于A,B两点,O是坐标原点,试求与直线l平行的抛物线的切线方程,并在弧 上求一点P,使△ABP的面积最大.解 设M(x0,y0)为切点,过点M与直线l平行的直线斜率为k=y′=2x0,
∴k=2x0=2,∴x0=1,y0 =1,故可得M(1,1),
∴切线方程为2x-y-1=0.
由于直线l: 2x-y+4=0与抛物线y=x2相交于A,B两点,
∴|AB|为定值,要使△ABP的面积最大,只要P到AB的距离最大,
故点M(1,1)即为所求弧 上的点,使△ABP的面积最大.核心素养之数学运算HEXINSUYANGZHISHUXUEYUNSUAN导数公式的应用典例 设f0(x)=sin x,f1(x)=f′0(x),f2(x)=f′1(x),…,fn+1(x)=f′n(x),n∈N,则f2 019(x)等于
A.sin x B.-sin x
C.cos x D.-cos x√解析 f1(x)=f′0(x)=(sin x)′=cos x,
f2(x)=f′1(x)=(cos x)′=-sin x,
f3(x)=f′2(x)=(-sin x)′=-cos x,
f4(x)=(-cos x)′=sin x,
f5(x)=(sin x)′=f1(x),
f6(x)=f2(x),…,
fn+4(x)=fn(x),
可知fn(x)关于n的周期为4,
∴f2 019(x)=f504×4+3(x)=-cos x.素养评析 熟记导数公式是进行导数运算的前提,正确的进行导数运算,方能找出规律,寻找到正确的结论.3达标检测PART THREE1.下列结论:
①(sin x)′=cos x;② ;
③(log3x)′= ;④(ln x)′= .
其中正确的有
A.0个 B.1个 C.2个 D.3个1234√∴②③错误,故选C.1234√3.设函数f(x)=logax,f′(1)=-1,则a=___.12342344.求过曲线y=sin x上的点 且与在这一点处的切线垂直的直线方程.1课堂小结KETANGXIAOJIE1.利用常见函数的导数公式可以比较简便地求出函数的导数,其关键是牢记和运用好导数公式.解题时,能认真观察函数的结构特征,积极地进行联想化归.3.对于正弦、余弦函数的导数,一是注意函数名称的变化,二是注意函数符号的变化.
