9.1.2 三角形的内角和与外角和 课件(15张PPT)
文档属性
| 名称 | 9.1.2 三角形的内角和与外角和 课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 189.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-29 00:00:00 | ||
图片预览



文档简介
课件15张PPT。2. 三角形的内角和与外角和内角三兄弟之争 在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起了……”“为什么?” 老二很纳闷。
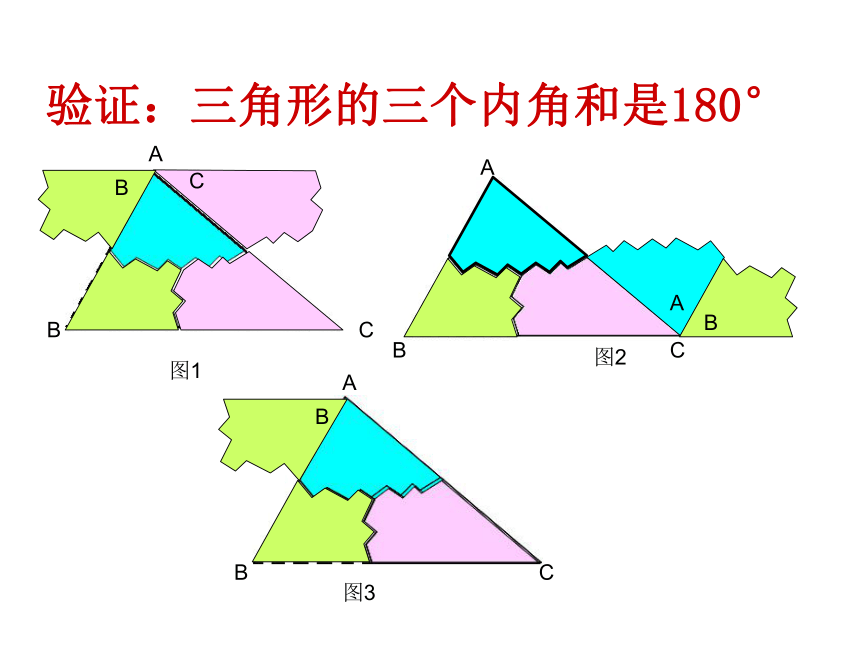
同学们,你们知道其中的道理吗?情境导入命题:三角形的三个内角和是180°你能验证这个命题吗?获取新知验证:三角形的三个内角和是180°图1图2 图3ABCAABBCC
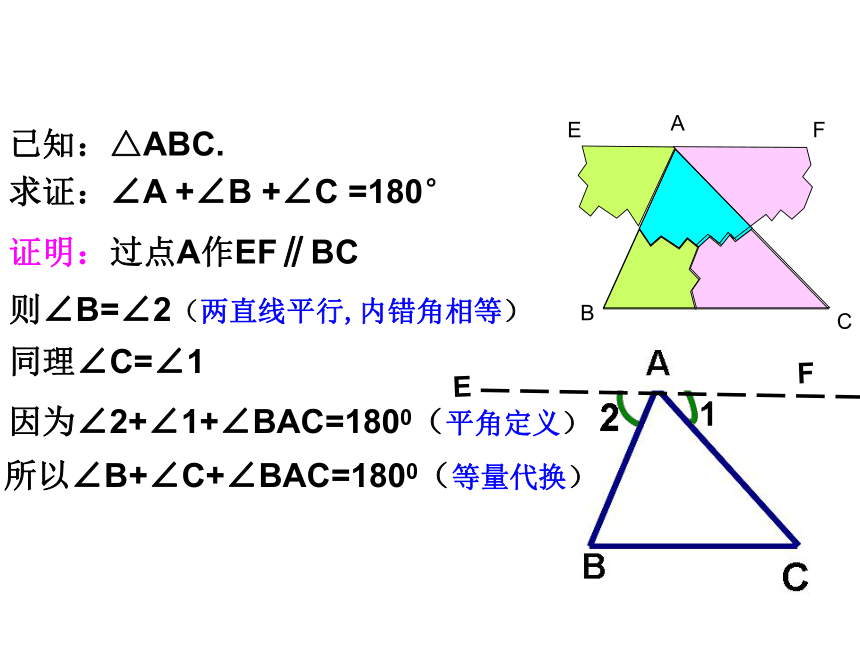
证明:过点A作EF∥BC则∠B=∠2(两直线平行,内错角相等)
同理∠C=∠1因为∠2+∠1+∠BAC=1800(平角定义) 所以∠B+∠C+∠BAC=1800(等量代换)已知:△ABC.求证:∠A +∠B +∠C =180°E F所以∠B+∠BAC +∠C =180°
(等量代换)已知:△ABC.
求证:
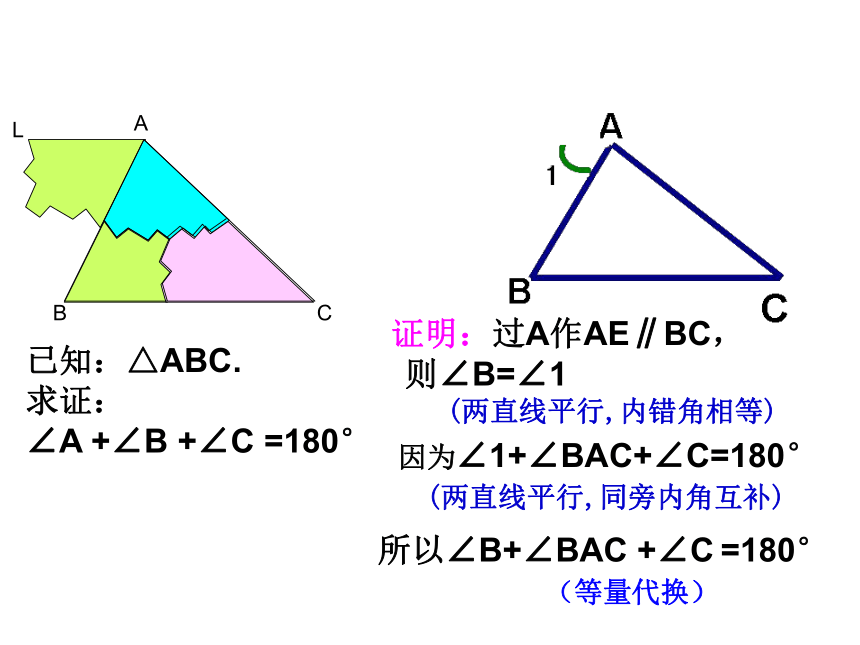
∠A +∠B +∠C =180°证明:过A作AE∥BC,则∠B=∠1
(两直线平行,内错角相等)因为∠1+∠BAC+∠C=180°
(两直线平行,同旁内角互补)定理:三角形的三个内角和是180°一个三角形中能有两个直角吗?
一个三角形中能有两个钝角吗?
三个内角都能小于600吗?
讨论∠1+ ∠2+ ∠3= 36001.(1)在△ABC中,∠A=35°,∠ B=43°,
则∠ C= . (2)在△ABC中,∠C=90°,∠B=50°,
则∠A = ____。(3)在△ABC中, ∠A=40°,∠A=2∠B,
则∠C = ____。10204001200随堂演练2.已知:三角形三个内角的度数之比为1:3:5,求这三个内角的度数。 解:设三个内角度数分别为:x、3x、5x,x+3x+5x=180°解得 x=20°所以三个内角度数分别为
20°,60°,100°。由三角形内角和为180°得 3.求出下列图中x的值: xx x x =600x x x =4502 x x┐x =3004、如图,直线AB∥CD,在AB、CD外有一点P,连结PB、PD交CD于E点。则∠ B、∠ D、∠ P 之间是否存在
一定的大小关系?ABCPDE他们是怎样的,并加以证明?证明:因为 AB ∥CD(1(2所以 ∠1 + ∠ B =1800
(两直线平行,同旁内角互补)因为∠2+ ∠P +∠D=1800
(三角形内角和定理)∠1= ∠2 (对顶角相等) 所以∠ B=∠P +∠D (等量代换) 5.三角形的三个外角之比为2:3:4,
则与它们相邻的内角分别为( ) A. 80? 120? 160 ? B. 160 ? 120 ? 80 ?
C. 100 ? 60 ? 20 ? D. 140 ? 120 ? 100 ? 解:设三角形的三个外角分别为2k,3k,4k,根据三角形的外角和等于360 ? ,有
2k+3k+4k= 360 ? , 可解得k=40 ?,三个外角分别为80? ,120? ,160 ? , 则相邻的内角分
别为100 ? , 60 ? , 20 ? .故选 CC本节课里你学到了什么???1、三角形内角和的定理:三角形三个内角的和等于180 °
2、通过思考、去探究、去总结三角形内角和的定理,并且发现要证明三角形三个内角的和等于180 °需
转化为:平角或两直线平行同旁内角和等于180°。3、三角形内角和的定理证明中,添加辅助线的实质是通过平行线来移动角。
课堂小结1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业
同学们,你们知道其中的道理吗?情境导入命题:三角形的三个内角和是180°你能验证这个命题吗?获取新知验证:三角形的三个内角和是180°图1图2 图3ABCAABBCC
证明:过点A作EF∥BC则∠B=∠2(两直线平行,内错角相等)
同理∠C=∠1因为∠2+∠1+∠BAC=1800(平角定义) 所以∠B+∠C+∠BAC=1800(等量代换)已知:△ABC.求证:∠A +∠B +∠C =180°E F所以∠B+∠BAC +∠C =180°
(等量代换)已知:△ABC.
求证:
∠A +∠B +∠C =180°证明:过A作AE∥BC,则∠B=∠1
(两直线平行,内错角相等)因为∠1+∠BAC+∠C=180°
(两直线平行,同旁内角互补)定理:三角形的三个内角和是180°一个三角形中能有两个直角吗?
一个三角形中能有两个钝角吗?
三个内角都能小于600吗?
讨论∠1+ ∠2+ ∠3= 36001.(1)在△ABC中,∠A=35°,∠ B=43°,
则∠ C= . (2)在△ABC中,∠C=90°,∠B=50°,
则∠A = ____。(3)在△ABC中, ∠A=40°,∠A=2∠B,
则∠C = ____。10204001200随堂演练2.已知:三角形三个内角的度数之比为1:3:5,求这三个内角的度数。 解:设三个内角度数分别为:x、3x、5x,x+3x+5x=180°解得 x=20°所以三个内角度数分别为
20°,60°,100°。由三角形内角和为180°得 3.求出下列图中x的值: xx x x =600x x x =4502 x x┐x =3004、如图,直线AB∥CD,在AB、CD外有一点P,连结PB、PD交CD于E点。则∠ B、∠ D、∠ P 之间是否存在
一定的大小关系?ABCPDE他们是怎样的,并加以证明?证明:因为 AB ∥CD(1(2所以 ∠1 + ∠ B =1800
(两直线平行,同旁内角互补)因为∠2+ ∠P +∠D=1800
(三角形内角和定理)∠1= ∠2 (对顶角相等) 所以∠ B=∠P +∠D (等量代换) 5.三角形的三个外角之比为2:3:4,
则与它们相邻的内角分别为( ) A. 80? 120? 160 ? B. 160 ? 120 ? 80 ?
C. 100 ? 60 ? 20 ? D. 140 ? 120 ? 100 ? 解:设三角形的三个外角分别为2k,3k,4k,根据三角形的外角和等于360 ? ,有
2k+3k+4k= 360 ? , 可解得k=40 ?,三个外角分别为80? ,120? ,160 ? , 则相邻的内角分
别为100 ? , 60 ? , 20 ? .故选 CC本节课里你学到了什么???1、三角形内角和的定理:三角形三个内角的和等于180 °
2、通过思考、去探究、去总结三角形内角和的定理,并且发现要证明三角形三个内角的和等于180 °需
转化为:平角或两直线平行同旁内角和等于180°。3、三角形内角和的定理证明中,添加辅助线的实质是通过平行线来移动角。
课堂小结1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业
