2020版高中数学新人教B版选修1-1第三章导数及其应用3.3.3导数的实际应用课件(40张PPT)
文档属性
| 名称 | 2020版高中数学新人教B版选修1-1第三章导数及其应用3.3.3导数的实际应用课件(40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-29 18:15:52 | ||
图片预览











文档简介
课件40张PPT。3.3.3 导数的实际应用第三章 导数及其应用学习目标XUEXIMUBIAO1.了解导数在解决实际问题中的作用.
2.掌握利用导数解决简单的实际生活中的优化问题.NEIRONGSUOYIN内容索引自主学习题型探究达标检测1自主学习PART ONE知识点 生活中的优化问题
1.生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为 .
2.利用导数解决优化问题的实质是求函数最值.
3.解决优化问题的基本思路:上述解决优化问题的过程是一个典型的 过程.优化问题数学建模1.生活中常见到的收益最高、用料最省等问题就是数学中的最大、最小值问题.( )
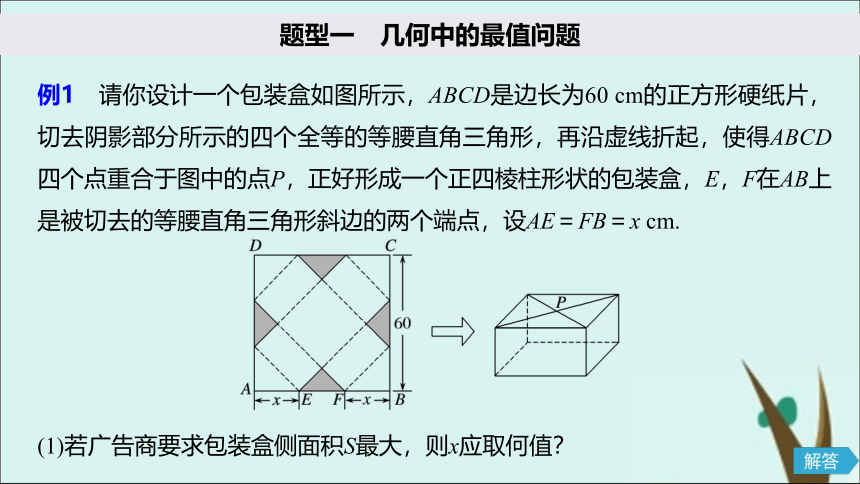
2.解决应用问题的关键是建立数学模型.( )思考辨析 判断正误SIKAOBIANXIPANDUANZHENGWU√√2题型探究PART TWO题型一 几何中的最值问题例1 请你设计一个包装盒如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E,F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x cm.(1)若广告商要求包装盒侧面积S最大,则x应取何值?当且仅当x=30-x,即x=15时,等号成立,
所以若广告商要求包装盒侧面积S最大,则x=15.(2)若广告商要求包装盒容积V最大,则x应取何值?并求出此时包装盒的高与底面边长的比值.令V′>0,得0所以当x=20时,包装盒容积V取得最大值,反思感悟 面积、体积(容积)最大,周长最短,距离最小等实际几何问题,求解时先设出恰当的变量,将待求解最值的问题表示为变量的函数,再按函数求最值的方法求解,最后检验.特别注意:在列函数关系式时,要注意实际问题中变量的取值范围,即函数的定义域.跟踪训练1 现需设计某次期中考试的数学试卷,该试卷含有大小相等的两个矩形栏目(即图中阴影部分),这两栏的面积之和为720 cm2,四周空白的宽度为4 cm,两栏之间的中缝空白的宽度为2 cm,设试卷的长和宽分别为x cm,y cm.
(1)写出y关于x的函数解析式,并求该函数的定义域;解 由题意知试卷的长和宽分别为x cm,y cm,(2)如何确定该试卷长与宽的尺寸(单位:cm),才能使试卷的面积最小?令S′=0,得x=40(负数舍去),
∴函数在(10,40)上单调递减,在(40,+∞)上单调递增,
∴当x=40时,S取得最小值,
故当试卷的长为40 cm,宽为32 cm时,可使试卷的面积最小.题型二 实际生活中的最值问题命题角度1 利润最大问题
例2 某工厂共有10台机器,生产一种仪器元件,由于受生产能力和技术水平等因素的限制,会产生一定数量的次品.根据经验知道,每台机器产生的次品数P(万件)与每台机器的日产量x(万件)(4≤x≤12)之间满足关系:P=0.1x2-3.2ln x+3.已知每生产1万件合格的元件可以盈利2万元,但每生产1万件次品将亏损1万元.(利润=盈利-亏损)
(1)试将该工厂每天生产这种元件所获得的利润y(万元)表示为x的函数;解 由题意得,所获得的利润为y=10[2(x-P)-P]=20x-3x2+96ln x-90(4≤x≤12).多维探究(2)当每台机器的日产量x(万件)为多少时所获得的利润最大,最大利润为多少?当4≤x≤6时,y′≥0,函数在[4,6]上为增函数;
当6≤x≤12时,y′≤0,函数在[6,12]上为减函数,
所以当x=6时,函数取得极大值,且为最大值,
最大利润为y=20×6-3×62+96ln 6-90=96ln 6-78(万元).反思感悟 解决此类有关利润的实际应用题,应灵活运用题设条件,建立利润的函数关系,常见的基本等量关系有:
(1)利润=收入-成本.
(2)利润=每件产品的利润×销售件数.跟踪训练2 某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y= +10(x-6)2,其中3<
x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求a的值;所以a=2.(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.解 由(1)可知,该商品每日的销售量所以商场每日销售该商品所获得的利润=2+10(x-3)(x-6)2,3从而f′(x)=10[(x-6)2+2(x-3)(x-6)]
=30(x-4)(x-6).于是,当x变化时,f′(x),f(x)的变化情况如下表:由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点.
所以当x=4时,函数f(x)取得最大值,且最大值为42.答 当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.命题角度2 用料(费用)最省问题
例3 某网球中心欲建连成片的网球场数块,用128万元购买土地10 000平方米,该中心每块球场的建设面积为1 000平方米,球场的总建筑面积的每平方米的平均建设费用与球场数有关,当该中心建球场x块时,每平方米的平均建设费用(单位:元)可近似地用f(x)=800 来刻画.为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和),该网球中心应建几个球场?令g′(x)=0,得x=8,当1≤x<8时,g′(x)<0,g(x)为减函数;当80,g(x)为增函数,
所以当x=8时,函数取得极小值,且为最小值.
故当建成8个球场时,每平方米的综合费用最省.反思感悟 费用、用料最省问题是日常生活中常见的问题之一,解决这类问题要明确自变量的意义以及最值问题所研究的对象.正确书写函数表达式,准确求导,结合实际作答.跟踪训练3 为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6 万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0≤x≤10),若不建隔热层,每年能源消耗费用为8 万元,设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式;且C(0)=8,故k=40,设建造费用为C1(x),则C1(x)=6x.(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.当0≤x<5时,f′(x)<0,f(x)为减函数;
当50,f(x)为增函数.故当隔热层修建厚度为5 cm时,总费用f(x)达到最小,最小值为70 万元.核心素养之数学建模HEXINSUYANGZHISHUXUEJIANMO损耗最少问题典例 已知A,B两地相距200千米,一艘船从A地逆水而行到B地,水速为
8 千米/时,船在静水中的速度为v 千米/时(80),则y1=kv2.
∵当v=12时,y1=720,∴720=k·122,得k=5.
设全程燃料费为y元,由题意,令y′=0,解得v=16.
若v0≥16,当v∈(8,16)时,y′<0,y为减函数;当v∈(16,v0]时,y′>0,y为增函数.
故当v=16时,y取得极小值,也是最小值,此时全程燃料费最省.
若v0<16,当v∈(8,v0]时,y′<0,y在(8,v0]上为减函数.
故当v=v0时,y取得最小值,此时全程燃料费最省.
综上可得,若v0≥16,则当v=16 千米/时时,全程燃料费最省;
若v0<16,则当v=v0时,全程燃料费最省.素养评析 (1)解决实际应用问题的关键在于建立数学模型和目标函数,把“问题情景”译为数学语言,要先找出问题的主要关系,并把问题的主要关系近似化、形式化、抽象成数学问题,再化归为常规问题,最后选择合适的数学方法求解.
(2)确定函数模型,将实际问题转化成数学问题的要求较高,有利于数学建模素养的提升.3达标检测PART THREE1234解析 原油温度的瞬时变化率为f′(x)=x2-2x=(x-1)2-1(0≤x≤5),
所以当x=1时,原油温度的瞬时变化率取得最小值-1.5√12342.用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2∶1,则该长方体的最大体积为
A.2 m3 B.3 m3 C.4 m3 D.5 m35√1234从而V′(x)=18x-18x2=18x(1-x),
令V′(x)=0,解得x=1或x=0(舍去).故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值,
从而最大体积V=V(1)=9×12-6×13=3(m3).53.某产品的销售收入y1(万元)是产品x(千台)的函数,y1=17x2(x>0);生产总成本y2(万元)也是x(千台)的函数,y2=2x3-x2(x>0),为使利润最大,则应生产
A.9 千台 B.8 千台 C.6 千台 D.3 千台√1234解析 利润y=y1-y2=17x2-(2x3-x2)=18x2-2x3(x>0),
求导得y′=36x-6x2,令y′=0,得x=6或x=0(舍去).
所以当生产6 千台时,利润最大.512344.容积为256的方底无盖水箱,它的高为 时最省材料.4解析 设水箱高为h,底面边长为a,则a2h=256,当08时,S′>0,512345.某商品每件成本9元,售价30元,每星期卖出432件.如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低额x(单位:元,0≤x≤21)的平方成正比.已知当商品单价降低2元时,每星期多卖出24件.
(1)将一个星期的商品销售利润表示成x的函数;解 设商品降价x元,则每星期多卖的商品数为kx2.
若记商品在一个星期的获利为f(x),则有
f(x)=(30-x-9)(432+kx2)=(21-x)(432+kx2).
由已知条件,得24=k×22,于是k=6.
所以f(x)=-6x3+126x2-432x+9 072,x∈[0,21].5(2)如何定价才能使一个星期的商品销售利润最大?解 由(1)得f′(x)=-18x2+252x-432
=-18(x-2)(x-12).
当x变化时,f′(x),f(x)的变化情况如下表:故当x=12时,f(x)取得极大值.
因为f(0)=9 072,f(12)=11 664.
所以当定价为30-12=18(元)时,才能使一个星期的商品销售利润最大.12345课堂小结KETANGXIAOJIE1.利用导数解决生活中优化问题的一般步骤
(1)分析实际问题中各量之间的关系,列出实际问题的数学模型,写出实际问题中变量之间的函数关系式y=f(x).
(2)求函数的导函数f′(x),解方程f′(x)=0.
(3)比较函数在区间端点和使f′(x)=0的点的函数值的大小,最大(小)者为最大(小)值.
2.正确理解题意,建立数学模型,利用导数求解是解答应用问题的主要思路.另外需要特别注意:(1)合理选择变量,正确写出函数解析式,给出函数定义域;(2)与实际问题相联系;(3)必要时注意分类讨论思想的应用.
2.掌握利用导数解决简单的实际生活中的优化问题.NEIRONGSUOYIN内容索引自主学习题型探究达标检测1自主学习PART ONE知识点 生活中的优化问题
1.生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为 .
2.利用导数解决优化问题的实质是求函数最值.
3.解决优化问题的基本思路:上述解决优化问题的过程是一个典型的 过程.优化问题数学建模1.生活中常见到的收益最高、用料最省等问题就是数学中的最大、最小值问题.( )
2.解决应用问题的关键是建立数学模型.( )思考辨析 判断正误SIKAOBIANXIPANDUANZHENGWU√√2题型探究PART TWO题型一 几何中的最值问题例1 请你设计一个包装盒如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E,F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x cm.(1)若广告商要求包装盒侧面积S最大,则x应取何值?当且仅当x=30-x,即x=15时,等号成立,
所以若广告商要求包装盒侧面积S最大,则x=15.(2)若广告商要求包装盒容积V最大,则x应取何值?并求出此时包装盒的高与底面边长的比值.令V′>0,得0
(1)写出y关于x的函数解析式,并求该函数的定义域;解 由题意知试卷的长和宽分别为x cm,y cm,(2)如何确定该试卷长与宽的尺寸(单位:cm),才能使试卷的面积最小?令S′=0,得x=40(负数舍去),
∴函数在(10,40)上单调递减,在(40,+∞)上单调递增,
∴当x=40时,S取得最小值,
故当试卷的长为40 cm,宽为32 cm时,可使试卷的面积最小.题型二 实际生活中的最值问题命题角度1 利润最大问题
例2 某工厂共有10台机器,生产一种仪器元件,由于受生产能力和技术水平等因素的限制,会产生一定数量的次品.根据经验知道,每台机器产生的次品数P(万件)与每台机器的日产量x(万件)(4≤x≤12)之间满足关系:P=0.1x2-3.2ln x+3.已知每生产1万件合格的元件可以盈利2万元,但每生产1万件次品将亏损1万元.(利润=盈利-亏损)
(1)试将该工厂每天生产这种元件所获得的利润y(万元)表示为x的函数;解 由题意得,所获得的利润为y=10[2(x-P)-P]=20x-3x2+96ln x-90(4≤x≤12).多维探究(2)当每台机器的日产量x(万件)为多少时所获得的利润最大,最大利润为多少?当4≤x≤6时,y′≥0,函数在[4,6]上为增函数;
当6≤x≤12时,y′≤0,函数在[6,12]上为减函数,
所以当x=6时,函数取得极大值,且为最大值,
最大利润为y=20×6-3×62+96ln 6-90=96ln 6-78(万元).反思感悟 解决此类有关利润的实际应用题,应灵活运用题设条件,建立利润的函数关系,常见的基本等量关系有:
(1)利润=收入-成本.
(2)利润=每件产品的利润×销售件数.跟踪训练2 某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y= +10(x-6)2,其中3<
x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求a的值;所以a=2.(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.解 由(1)可知,该商品每日的销售量所以商场每日销售该商品所获得的利润=2+10(x-3)(x-6)2,3
=30(x-4)(x-6).于是,当x变化时,f′(x),f(x)的变化情况如下表:由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点.
所以当x=4时,函数f(x)取得最大值,且最大值为42.答 当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.命题角度2 用料(费用)最省问题
例3 某网球中心欲建连成片的网球场数块,用128万元购买土地10 000平方米,该中心每块球场的建设面积为1 000平方米,球场的总建筑面积的每平方米的平均建设费用与球场数有关,当该中心建球场x块时,每平方米的平均建设费用(单位:元)可近似地用f(x)=800 来刻画.为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和),该网球中心应建几个球场?令g′(x)=0,得x=8,当1≤x<8时,g′(x)<0,g(x)为减函数;当8
所以当x=8时,函数取得极小值,且为最小值.
故当建成8个球场时,每平方米的综合费用最省.反思感悟 费用、用料最省问题是日常生活中常见的问题之一,解决这类问题要明确自变量的意义以及最值问题所研究的对象.正确书写函数表达式,准确求导,结合实际作答.跟踪训练3 为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6 万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0≤x≤10),若不建隔热层,每年能源消耗费用为8 万元,设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式;且C(0)=8,故k=40,设建造费用为C1(x),则C1(x)=6x.(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.当0≤x<5时,f′(x)<0,f(x)为减函数;
当5
8 千米/时,船在静水中的速度为v 千米/时(8
∵当v=12时,y1=720,∴720=k·122,得k=5.
设全程燃料费为y元,由题意,令y′=0,解得v=16.
若v0≥16,当v∈(8,16)时,y′<0,y为减函数;当v∈(16,v0]时,y′>0,y为增函数.
故当v=16时,y取得极小值,也是最小值,此时全程燃料费最省.
若v0<16,当v∈(8,v0]时,y′<0,y在(8,v0]上为减函数.
故当v=v0时,y取得最小值,此时全程燃料费最省.
综上可得,若v0≥16,则当v=16 千米/时时,全程燃料费最省;
若v0<16,则当v=v0时,全程燃料费最省.素养评析 (1)解决实际应用问题的关键在于建立数学模型和目标函数,把“问题情景”译为数学语言,要先找出问题的主要关系,并把问题的主要关系近似化、形式化、抽象成数学问题,再化归为常规问题,最后选择合适的数学方法求解.
(2)确定函数模型,将实际问题转化成数学问题的要求较高,有利于数学建模素养的提升.3达标检测PART THREE1234解析 原油温度的瞬时变化率为f′(x)=x2-2x=(x-1)2-1(0≤x≤5),
所以当x=1时,原油温度的瞬时变化率取得最小值-1.5√12342.用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2∶1,则该长方体的最大体积为
A.2 m3 B.3 m3 C.4 m3 D.5 m35√1234从而V′(x)=18x-18x2=18x(1-x),
令V′(x)=0,解得x=1或x=0(舍去).故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值,
从而最大体积V=V(1)=9×12-6×13=3(m3).53.某产品的销售收入y1(万元)是产品x(千台)的函数,y1=17x2(x>0);生产总成本y2(万元)也是x(千台)的函数,y2=2x3-x2(x>0),为使利润最大,则应生产
A.9 千台 B.8 千台 C.6 千台 D.3 千台√1234解析 利润y=y1-y2=17x2-(2x3-x2)=18x2-2x3(x>0),
求导得y′=36x-6x2,令y′=0,得x=6或x=0(舍去).
所以当生产6 千台时,利润最大.512344.容积为256的方底无盖水箱,它的高为 时最省材料.4解析 设水箱高为h,底面边长为a,则a2h=256,当0
(1)将一个星期的商品销售利润表示成x的函数;解 设商品降价x元,则每星期多卖的商品数为kx2.
若记商品在一个星期的获利为f(x),则有
f(x)=(30-x-9)(432+kx2)=(21-x)(432+kx2).
由已知条件,得24=k×22,于是k=6.
所以f(x)=-6x3+126x2-432x+9 072,x∈[0,21].5(2)如何定价才能使一个星期的商品销售利润最大?解 由(1)得f′(x)=-18x2+252x-432
=-18(x-2)(x-12).
当x变化时,f′(x),f(x)的变化情况如下表:故当x=12时,f(x)取得极大值.
因为f(0)=9 072,f(12)=11 664.
所以当定价为30-12=18(元)时,才能使一个星期的商品销售利润最大.12345课堂小结KETANGXIAOJIE1.利用导数解决生活中优化问题的一般步骤
(1)分析实际问题中各量之间的关系,列出实际问题的数学模型,写出实际问题中变量之间的函数关系式y=f(x).
(2)求函数的导函数f′(x),解方程f′(x)=0.
(3)比较函数在区间端点和使f′(x)=0的点的函数值的大小,最大(小)者为最大(小)值.
2.正确理解题意,建立数学模型,利用导数求解是解答应用问题的主要思路.另外需要特别注意:(1)合理选择变量,正确写出函数解析式,给出函数定义域;(2)与实际问题相联系;(3)必要时注意分类讨论思想的应用.
