9.1.3 三角形的三边关系 课件(15张PPT)
文档属性
| 名称 | 9.1.3 三角形的三边关系 课件(15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 231.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 08:41:55 | ||
图片预览






文档简介
课件15张PPT。三角形的三边关系复习旧知1.三角形的定义是什么?
2.三角形按边分类可分为什么?
3.三角形的内角和和外角和分别是 多少?
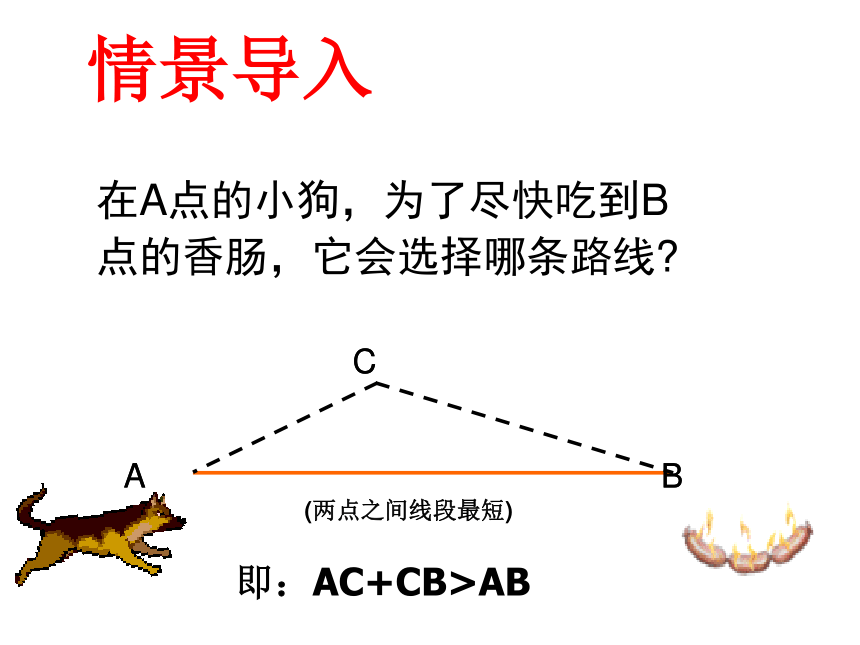
4.线段的基本事实是什么?情景导入即:AC+CB>AB在A点的小狗,为了尽快吃到B点的香肠,它会选择哪条路线?
(两点之间线段最短)9.1.3 三角形的三边关系学习目标:1.掌握三角形三条边的大小关系;
2.会应用三角形三边关系处理问题;
3.了解三角形的稳定性. 现有长18cm,15cm,6cm,9cm的四根小棒,你任意选三根,看能否围成三角形。若不是,哪些可以?哪些不可以?
通过拼图,你发现能拼成三角形的每两边的和总是——第三边,而不能拼成三角形的三根木棒,会出现两边之和——或——第三边。1、拼一拼以下列长度的各组线段为边,画一个三角形.2、画一画 (1)6cm,4cm,3cm;(2)5cm,2cm,3cm;(3)6cm,3cm,2cm;由作图可知,你发现了什么结论?
概括:三角形的三边关系:————说出你的方法。(3)3 cm、8 cm、5 cm;(4)4 cm、5 cm、6 cm.(1) 15cm、10 cm、7 cm;(2)4 cm、5 cm、10 cm;下列长度的各组线段能否组成一个三角形? 3、想一想将上面各式b+c>a,a+b>c,a+c>b移项得:b____a-c ; a ____ c-b; c____ b-a
于是有:三角形的任何两边的差____第三边
所以得三角形第三边的范围:
其它两边的差______第三边______其它两边的和
4、知识拓展:5、思考7、三角形的稳定性
(1)演示最简单教具:木条钉成的三角形和四边形,用力一拉四边形变形了,而三角形却一点不变,学生直接感受;
(2)给出概念;
(3)举出三角形的稳定性在生产,生活中应用的例子;
1.下列长度的三条线段能组成三角形的是( )
A.5,6,10 B.5,6,11
C.3,4,8 D.4a,4a,8a(a>0)
2.一个三角形的三条边长分别为1,2,x, 则x的取值范围是——
3.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B.6
C.12 D.16
课堂练习已知△ABC的两边AB=2cm,AC=9 cm.
(1)求第三边BC长的取值范围;
(2)若第三边BC的长是偶数,BC的长;
(3)若△ ABC是等腰三角形,求其周长
能力提升课堂小结:1、三角形的三边关系。
2、三角形的稳定性。谢谢
2.三角形按边分类可分为什么?
3.三角形的内角和和外角和分别是 多少?
4.线段的基本事实是什么?情景导入即:AC+CB>AB在A点的小狗,为了尽快吃到B点的香肠,它会选择哪条路线?
(两点之间线段最短)9.1.3 三角形的三边关系学习目标:1.掌握三角形三条边的大小关系;
2.会应用三角形三边关系处理问题;
3.了解三角形的稳定性. 现有长18cm,15cm,6cm,9cm的四根小棒,你任意选三根,看能否围成三角形。若不是,哪些可以?哪些不可以?
通过拼图,你发现能拼成三角形的每两边的和总是——第三边,而不能拼成三角形的三根木棒,会出现两边之和——或——第三边。1、拼一拼以下列长度的各组线段为边,画一个三角形.2、画一画 (1)6cm,4cm,3cm;(2)5cm,2cm,3cm;(3)6cm,3cm,2cm;由作图可知,你发现了什么结论?
概括:三角形的三边关系:————说出你的方法。(3)3 cm、8 cm、5 cm;(4)4 cm、5 cm、6 cm.(1) 15cm、10 cm、7 cm;(2)4 cm、5 cm、10 cm;下列长度的各组线段能否组成一个三角形? 3、想一想将上面各式b+c>a,a+b>c,a+c>b移项得:b____a-c ; a ____ c-b; c____ b-a
于是有:三角形的任何两边的差____第三边
所以得三角形第三边的范围:
其它两边的差______第三边______其它两边的和
4、知识拓展:5、思考7、三角形的稳定性
(1)演示最简单教具:木条钉成的三角形和四边形,用力一拉四边形变形了,而三角形却一点不变,学生直接感受;
(2)给出概念;
(3)举出三角形的稳定性在生产,生活中应用的例子;
1.下列长度的三条线段能组成三角形的是( )
A.5,6,10 B.5,6,11
C.3,4,8 D.4a,4a,8a(a>0)
2.一个三角形的三条边长分别为1,2,x, 则x的取值范围是——
3.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B.6
C.12 D.16
课堂练习已知△ABC的两边AB=2cm,AC=9 cm.
(1)求第三边BC长的取值范围;
(2)若第三边BC的长是偶数,BC的长;
(3)若△ ABC是等腰三角形,求其周长
能力提升课堂小结:1、三角形的三边关系。
2、三角形的稳定性。谢谢
