9.3.1 用相同的正多边形 课件(16张PPT)
文档属性
| 名称 | 9.3.1 用相同的正多边形 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 898.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 08:41:55 | ||
图片预览





文档简介
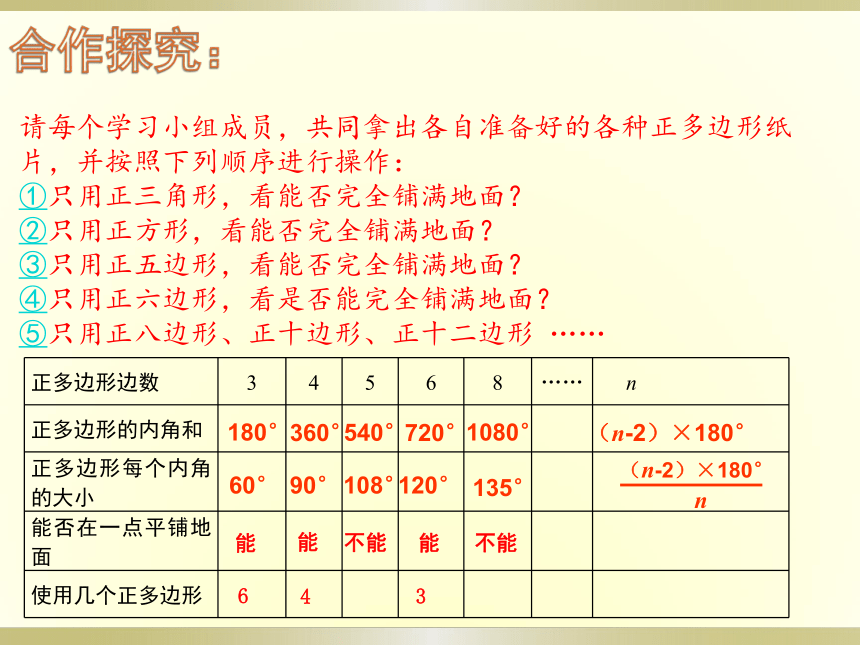
课件16张PPT。留意我们周围的墙面和地面是用什么形状的板砖拼铺而成的?9.3用正多边形铺设地面1 用相同的正多边形各边都相等,各内角也都相等的多边形叫做正多边形。回顾概念什么是正多边形?n边形的内角和公式:(n-2) ·180°正n边形的每个内角度数:观察这些美丽的图案,你有什么发现?平面密铺:用形状大小相同的多边形拼接在一起,既不留空隙又不互相重叠,这就称为平面图形的密铺也称镶嵌.合作探究:请每个学习小组成员,共同拿出各自准备好的各种正多边形纸片,并按照下列顺序进行操作:
①只用正三角形,看能否完全铺满地面?
②只用正方形,看能否完全铺满地面?
③只用正五边形,看能否完全铺满地面?
④只用正六边形,看是否能完全铺满地面?
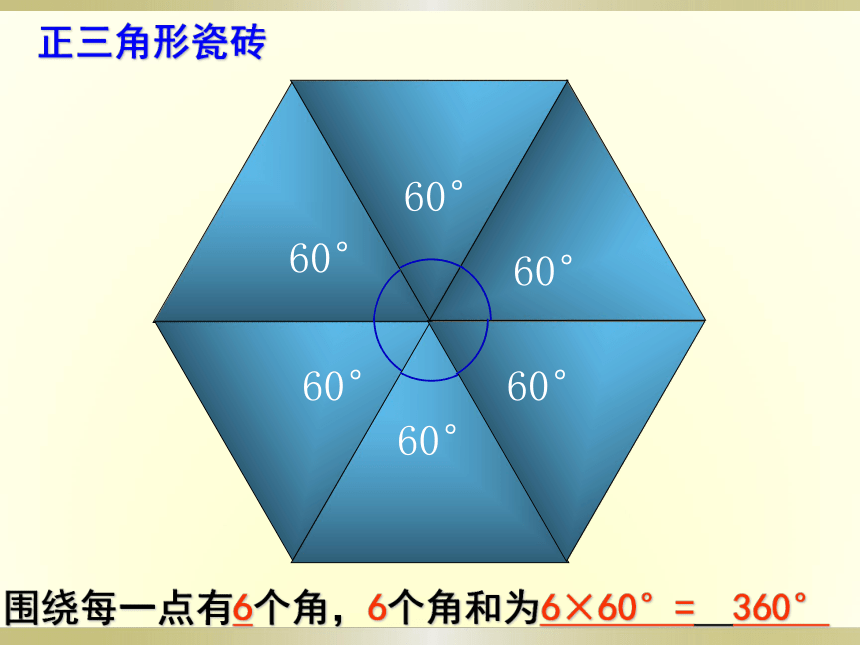
⑤只用正八边形、正十边形、正十二边形 ……180°60°360°90°540°108°720°120°1080° 135°(n-2)×180°能能不能能不能64360°60°60°60°60°60°正三角形瓷砖围绕每一点有6个角,6个角和为6×60°= 360°90°90°90°90°正方形瓷砖围绕每一点有4个角,4个角和为4×90°=360°108°108°108°正五边形瓷砖围绕每一点有3个角,3个角和为3×108°= 324°≠360°120°120°120°正六边形瓷砖围绕每一点有3个角,3个角和为3×120°=360°正七边形正八边形呢?想一想,为什么?不能!也不能!>360°>360°正八边形的每个内角为 (8-2) ×180°÷8=135°围绕每一点有3个角,3个角和为3×135°=405°正七边形的每个内角为 (7-2) ×180°÷7≈128.6°围绕每一点有3个角,3个角和为3×128.6°=385.8°思考:为什么有的正多边形能铺满地面,有的却不行呢? 规律:
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。归纳小结:2、正多边形密铺满足的条件:
正多边形的每个内角度数能整除360°.3、能用同一种正多边形铺设地面的正多边形
有 . 正三角形、正方形、正六边形1、能拼成既不留空隙,又不重叠的平面图形的关键是围绕一点拼在一起的几个多边形的内角相加恰好等于 °.
360头脑风暴任意一种三角形,任意一种四边形是否都能密铺?练习:例1. 若铺满地面的瓷砖每 一顶点处由6块相同的正多边形组成,此时的正多边形只能是( ).
A.正三角形 B.正四边形 C.正六边形 D.正八边形
例2. 用一种正多边形能进行平面图形密铺的条件是( ).
A.内角都是整数度数 B.边数是3的整数倍
C.内角整除360° D.内角整除180°
例3.如图用三个完全相同的正五边形地砖平铺地面,则空余的角度是 o.例4.下列五种正多边形地砖:① 正三角形;② 正方形;③ 正五边形;④ 正六边形;⑤ 正八边形,现要用同一种大小一样、形状相同的正多边形地砖铺设地面,其中能做到彼此之间不留空隙、不重叠地铺设的地砖有 种.
例5. 利用边长相等的正六边形材料,铺成平整无空隙的地面时,在每个顶点处有a个正六边形,则a等于( ).
A. 3 B. 4 C. 5 D. 6
例6. 用4个全等的正八边形进行拼接,使相等的两个正八边形有一条公共边,围成一圈后中间 形成一个正方形,用n个全等的正六边形按这种方式进行拼接,若围成一圈后中间形成一个正多边形,则n的值为 .
①只用正三角形,看能否完全铺满地面?
②只用正方形,看能否完全铺满地面?
③只用正五边形,看能否完全铺满地面?
④只用正六边形,看是否能完全铺满地面?
⑤只用正八边形、正十边形、正十二边形 ……180°60°360°90°540°108°720°120°1080° 135°(n-2)×180°能能不能能不能64360°60°60°60°60°60°正三角形瓷砖围绕每一点有6个角,6个角和为6×60°= 360°90°90°90°90°正方形瓷砖围绕每一点有4个角,4个角和为4×90°=360°108°108°108°正五边形瓷砖围绕每一点有3个角,3个角和为3×108°= 324°≠360°120°120°120°正六边形瓷砖围绕每一点有3个角,3个角和为3×120°=360°正七边形正八边形呢?想一想,为什么?不能!也不能!>360°>360°正八边形的每个内角为 (8-2) ×180°÷8=135°围绕每一点有3个角,3个角和为3×135°=405°正七边形的每个内角为 (7-2) ×180°÷7≈128.6°围绕每一点有3个角,3个角和为3×128.6°=385.8°思考:为什么有的正多边形能铺满地面,有的却不行呢? 规律:
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。归纳小结:2、正多边形密铺满足的条件:
正多边形的每个内角度数能整除360°.3、能用同一种正多边形铺设地面的正多边形
有 . 正三角形、正方形、正六边形1、能拼成既不留空隙,又不重叠的平面图形的关键是围绕一点拼在一起的几个多边形的内角相加恰好等于 °.
360头脑风暴任意一种三角形,任意一种四边形是否都能密铺?练习:例1. 若铺满地面的瓷砖每 一顶点处由6块相同的正多边形组成,此时的正多边形只能是( ).
A.正三角形 B.正四边形 C.正六边形 D.正八边形
例2. 用一种正多边形能进行平面图形密铺的条件是( ).
A.内角都是整数度数 B.边数是3的整数倍
C.内角整除360° D.内角整除180°
例3.如图用三个完全相同的正五边形地砖平铺地面,则空余的角度是 o.例4.下列五种正多边形地砖:① 正三角形;② 正方形;③ 正五边形;④ 正六边形;⑤ 正八边形,现要用同一种大小一样、形状相同的正多边形地砖铺设地面,其中能做到彼此之间不留空隙、不重叠地铺设的地砖有 种.
例5. 利用边长相等的正六边形材料,铺成平整无空隙的地面时,在每个顶点处有a个正六边形,则a等于( ).
A. 3 B. 4 C. 5 D. 6
例6. 用4个全等的正八边形进行拼接,使相等的两个正八边形有一条公共边,围成一圈后中间 形成一个正方形,用n个全等的正六边形按这种方式进行拼接,若围成一圈后中间形成一个正多边形,则n的值为 .
