9.3.2用多种正多边形 课件(39张PPT)
文档属性
| 名称 | 9.3.2用多种正多边形 课件(39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 681.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 00:00:00 | ||
图片预览



文档简介
课件39张PPT。9.3 用正多边形铺设地面(2)复习引入1、当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个___时,就拼成一个平面图形2、下列图形中不能铺满地面的是( ):A.正三角形 B.正方形
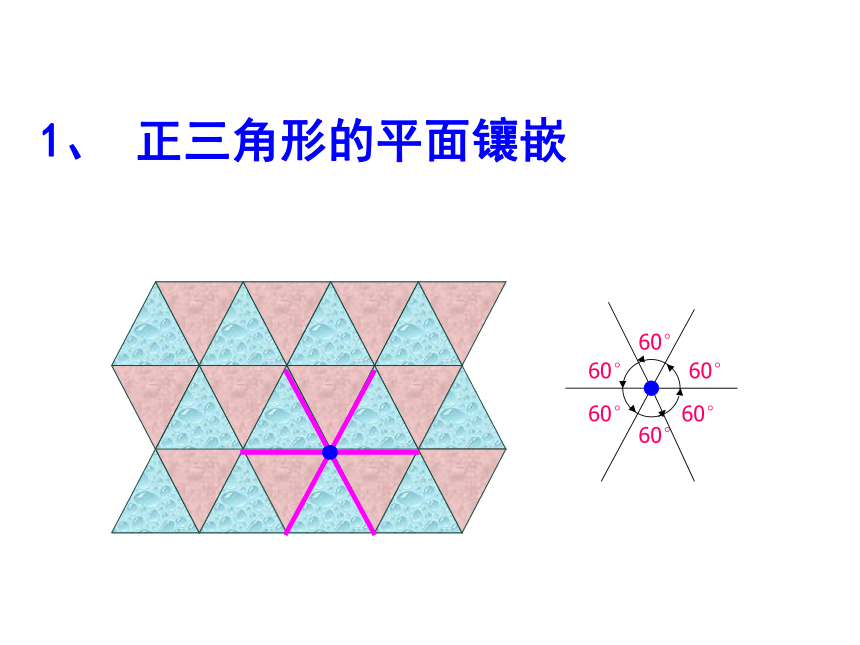
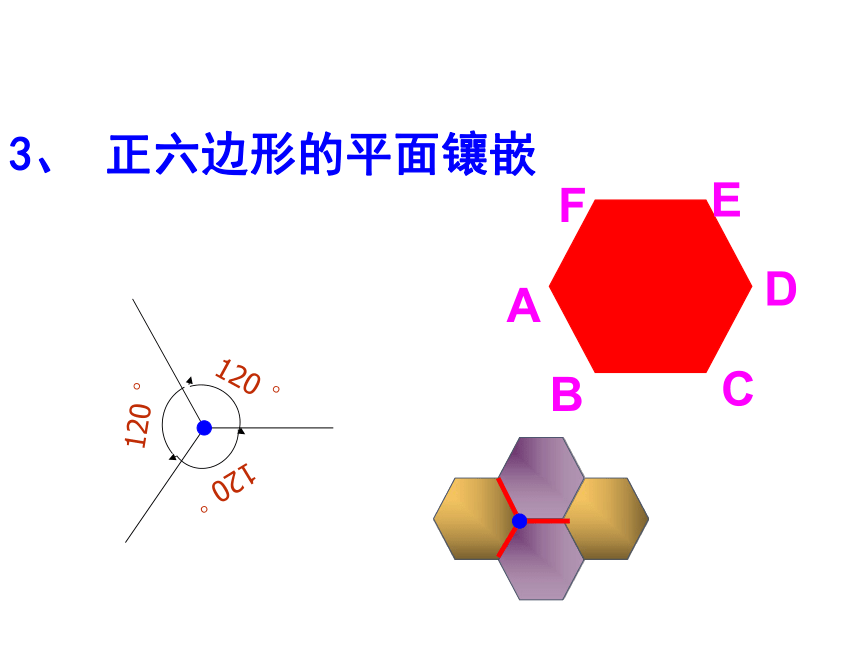
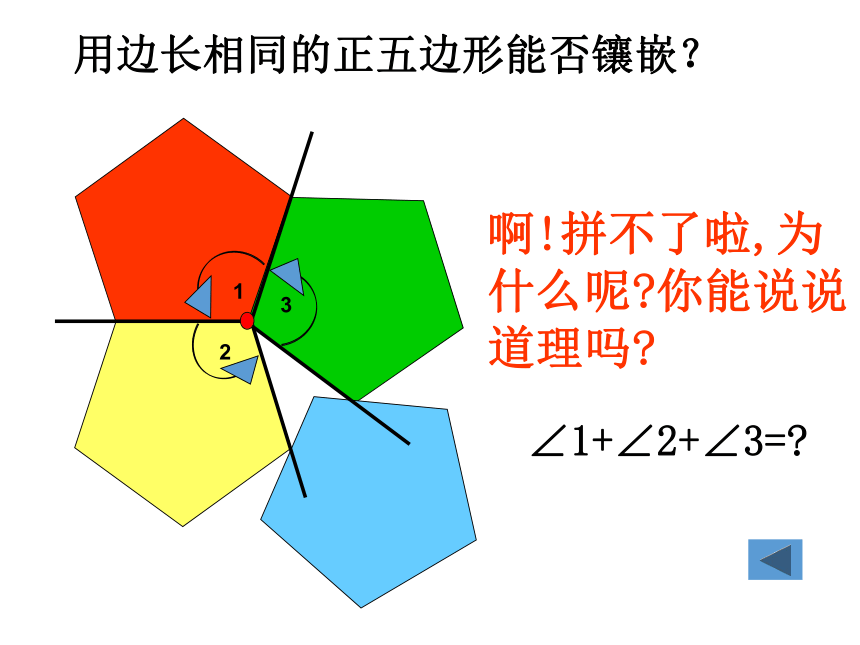
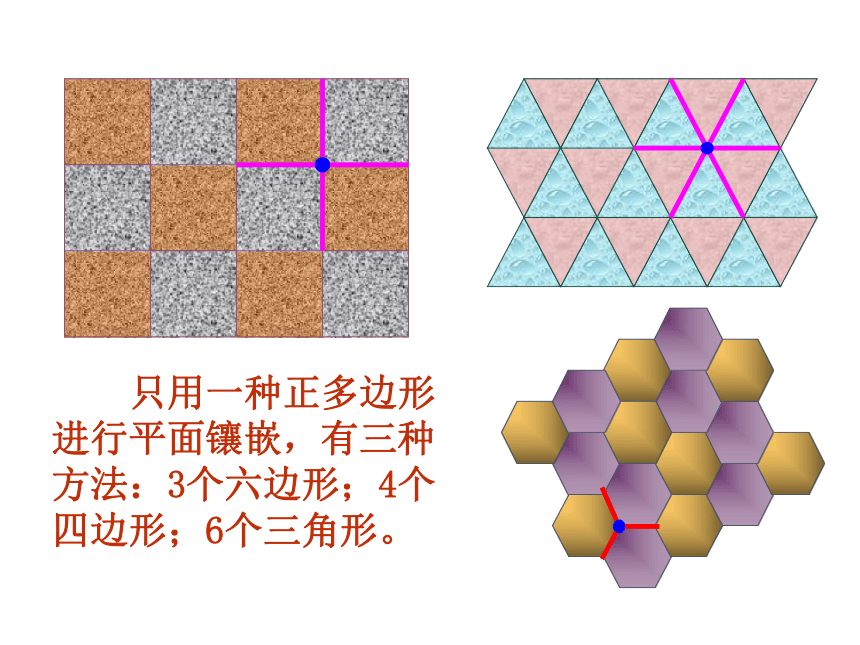
C.正六边形 D.正五边形1、 正三角形的平面镶嵌2、 正方形的平面镶嵌90°3、 正六边形的平面镶嵌120 °120 °120 °啊!拼不了啦,为什么呢?你能说说道理吗?123∠1+∠2+∠3=?用边长相同的正五边形能否镶嵌? 只用一种正多边形进行平面镶嵌,有三种方法:3个六边形;4个四边形;6个三角形。 ∵ ∠1+∠2+∠3=180°
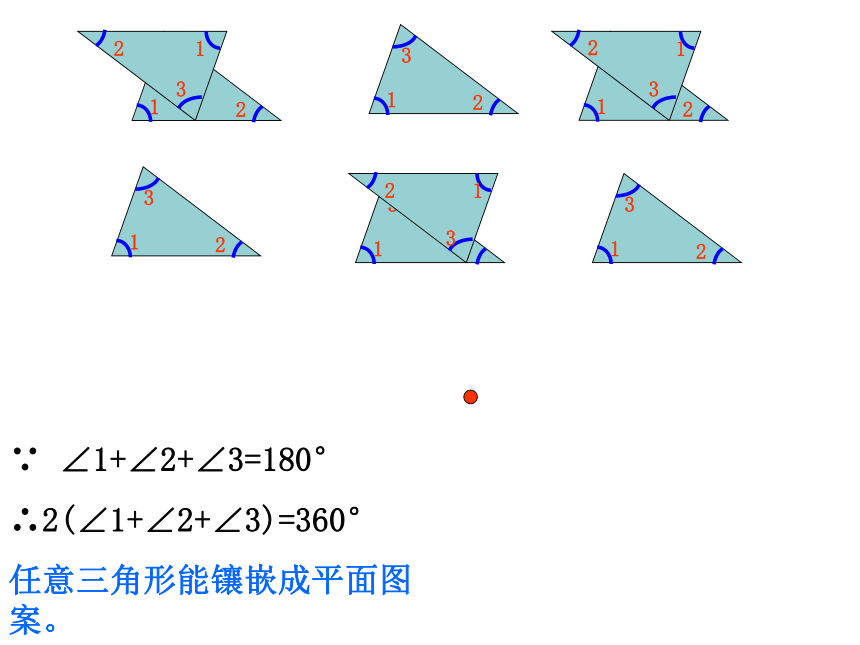
∴2(∠1+∠2+∠3)=360°
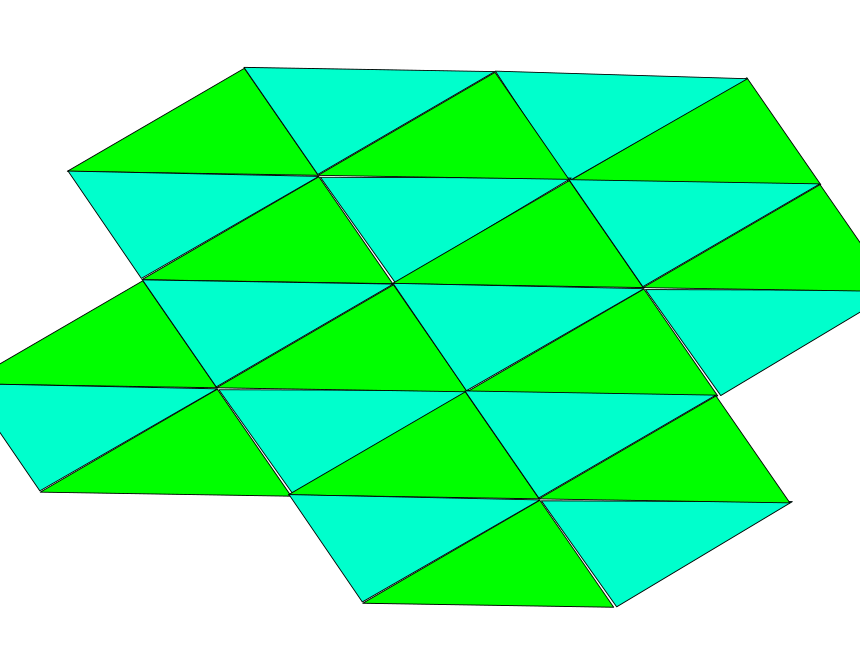
任意三角形能镶嵌成平面图案。如图,四边形ABCD中,因为∠A+∠B+∠C+ ∠D = 360°,所以
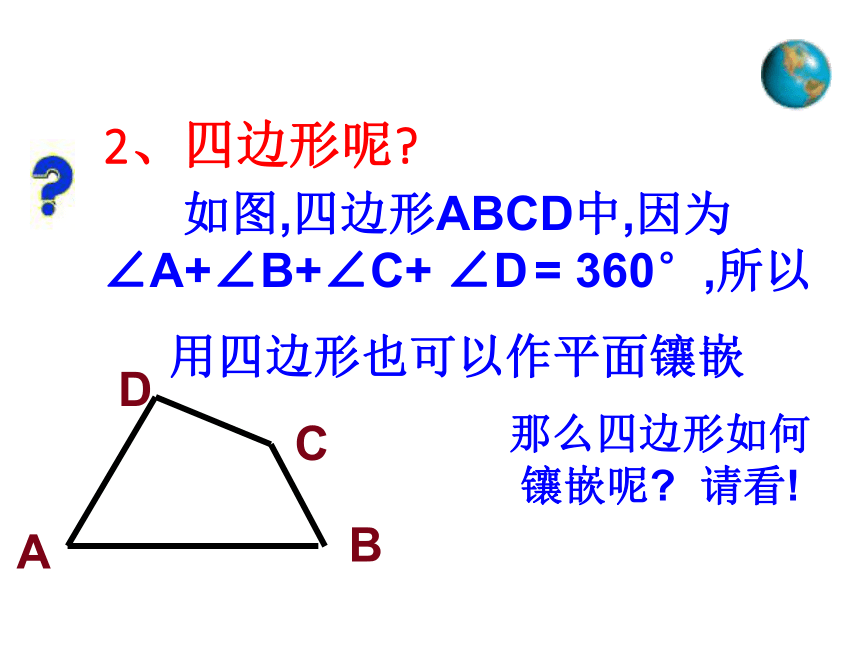
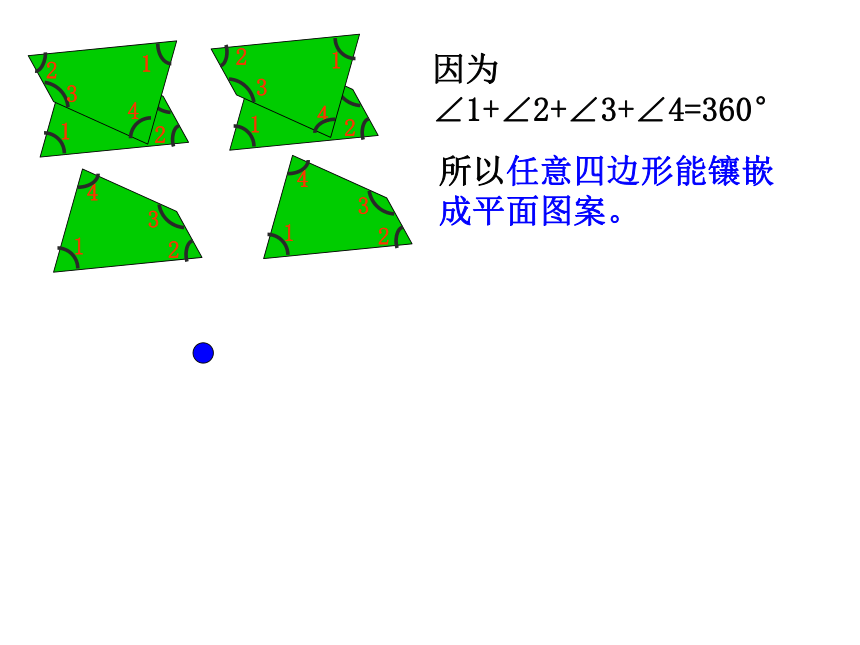
用四边形也可以作平面镶嵌2、四边形呢?那么四边形如何镶嵌呢? 请看!因为∠1+∠2+∠3+∠4=360°所以任意四边形能镶嵌成平面图案。
探究:几种多边形的混合铺设地面下列多边形组合,能够铺满地面的是:
(1)正三角形与正六边形;
(2)正三角形与正方形;
(3)正方形与正八边形;
(4)正六边形与正八边形;
(5)正三角形、正方形与正六边形。设在一个顶点周围有m个正三角形,n个正方形的角。②注意:同一个组合会有不同的镶嵌效果一、两种正多边形铺设地面(1) 正三角形与正方形的平面镶嵌120°120°60°60°图案(Ⅰ)设在一个顶点周围有m个正三角形,n个正六边形的角。(2)正三角形与正六边形的平面镶嵌图案(Ⅱ)60°60°120°60°60°(2)正三角形与正六边形的平面镶嵌每个顶点处正三角形4个,正六边形1个。(3)正三角形和正十二边形平面镶嵌图案2m+5n=12m=1
n=2设在一个顶点周围有m个正三角形的角、
n个正十二边形的角,则有∵m、n为正整数∴解为更多的两种正多边形的镶嵌正十边形与正五边形的平面镶嵌尽管能围绕一点拼成360o,但不能扩展到整个平面。1、正六边形、正方形和正三角形的组合。探究3:用三种正多边形合在一起拼地板2、正十二边形、正六边形和正方形的组合。 1. 由多种正多边形组合起来铺满地面的条件:围绕
一点拼在一起的各个正多边形的几个内角相加后
和为 360°.
2. 用两种正多边形铺满地面的常见种类有:
(1)正三角形和正方形;(2)正三角形和正六边形;
(3)正三角形和正十二边形;(4)正方形和正八边形.
3. 用三种正多边形铺满地面的常见种类有:
(1)正三角形、正方形和正六边形;
(2)正方形、正六边形和正十二边形.小结与反思1用几种正多边形能密铺的条件是围绕一点拼在一起的几个正多边形各内角的和恰好是( )
A.45° B.90°
C.180° D.360°
小李家装修地面,已有正三角形的地砖,现打算购买另一种不同形状的正多边形地砖,用这两种地砖铺地面,则小李不应购买的地砖形状是( )
A.正方形 B.正六边形
C.正八边形 D.正十二边形2课堂练习3、下列组合中,能铺满地面的是( )
A . 边长相等的正方形和正六边形
B . 边长相等的正方形和正三角形
C .边长相等的正方形和正五边形
D . 边长相等的正方形和正八边形4、用下列一种或两种正多边形铺地面:
(1)正三角形,
(2)正八边形,
(3)正三角形和正八边形,
(4)正六边形和正十二边形,
(5)正五边形和正十边形,
(6)正六边形和正八边形;
能铺满地面的有( )
A .2种 B .3种 C .4种 D .5种5下列美妙的图案中,是由正三角形、正方形、正六边形、正八边形中的三种密铺而成的为( )生活中利用镶嵌组成的美丽图案计算机绘制的镶嵌图片欣赏:计算机绘制的镶嵌图片欣赏:计算机绘制的镶嵌图片欣赏:再见!
C.正六边形 D.正五边形1、 正三角形的平面镶嵌2、 正方形的平面镶嵌90°3、 正六边形的平面镶嵌120 °120 °120 °啊!拼不了啦,为什么呢?你能说说道理吗?123∠1+∠2+∠3=?用边长相同的正五边形能否镶嵌? 只用一种正多边形进行平面镶嵌,有三种方法:3个六边形;4个四边形;6个三角形。 ∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
任意三角形能镶嵌成平面图案。如图,四边形ABCD中,因为∠A+∠B+∠C+ ∠D = 360°,所以
用四边形也可以作平面镶嵌2、四边形呢?那么四边形如何镶嵌呢? 请看!因为∠1+∠2+∠3+∠4=360°所以任意四边形能镶嵌成平面图案。
探究:几种多边形的混合铺设地面下列多边形组合,能够铺满地面的是:
(1)正三角形与正六边形;
(2)正三角形与正方形;
(3)正方形与正八边形;
(4)正六边形与正八边形;
(5)正三角形、正方形与正六边形。设在一个顶点周围有m个正三角形,n个正方形的角。②注意:同一个组合会有不同的镶嵌效果一、两种正多边形铺设地面(1) 正三角形与正方形的平面镶嵌120°120°60°60°图案(Ⅰ)设在一个顶点周围有m个正三角形,n个正六边形的角。(2)正三角形与正六边形的平面镶嵌图案(Ⅱ)60°60°120°60°60°(2)正三角形与正六边形的平面镶嵌每个顶点处正三角形4个,正六边形1个。(3)正三角形和正十二边形平面镶嵌图案2m+5n=12m=1
n=2设在一个顶点周围有m个正三角形的角、
n个正十二边形的角,则有∵m、n为正整数∴解为更多的两种正多边形的镶嵌正十边形与正五边形的平面镶嵌尽管能围绕一点拼成360o,但不能扩展到整个平面。1、正六边形、正方形和正三角形的组合。探究3:用三种正多边形合在一起拼地板2、正十二边形、正六边形和正方形的组合。 1. 由多种正多边形组合起来铺满地面的条件:围绕
一点拼在一起的各个正多边形的几个内角相加后
和为 360°.
2. 用两种正多边形铺满地面的常见种类有:
(1)正三角形和正方形;(2)正三角形和正六边形;
(3)正三角形和正十二边形;(4)正方形和正八边形.
3. 用三种正多边形铺满地面的常见种类有:
(1)正三角形、正方形和正六边形;
(2)正方形、正六边形和正十二边形.小结与反思1用几种正多边形能密铺的条件是围绕一点拼在一起的几个正多边形各内角的和恰好是( )
A.45° B.90°
C.180° D.360°
小李家装修地面,已有正三角形的地砖,现打算购买另一种不同形状的正多边形地砖,用这两种地砖铺地面,则小李不应购买的地砖形状是( )
A.正方形 B.正六边形
C.正八边形 D.正十二边形2课堂练习3、下列组合中,能铺满地面的是( )
A . 边长相等的正方形和正六边形
B . 边长相等的正方形和正三角形
C .边长相等的正方形和正五边形
D . 边长相等的正方形和正八边形4、用下列一种或两种正多边形铺地面:
(1)正三角形,
(2)正八边形,
(3)正三角形和正八边形,
(4)正六边形和正十二边形,
(5)正五边形和正十边形,
(6)正六边形和正八边形;
能铺满地面的有( )
A .2种 B .3种 C .4种 D .5种5下列美妙的图案中,是由正三角形、正方形、正六边形、正八边形中的三种密铺而成的为( )生活中利用镶嵌组成的美丽图案计算机绘制的镶嵌图片欣赏:计算机绘制的镶嵌图片欣赏:计算机绘制的镶嵌图片欣赏:再见!
