9.3 用正多边形铺设地面 课件(18张PPT)
文档属性
| 名称 | 9.3 用正多边形铺设地面 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 00:00:00 | ||
图片预览



文档简介
课件18张PPT。
用正多边形铺设地面华东师大版
七年级数观察发现
探索新知 用正多边形能够铺设地面的实质是指什么呢?
是指用某种正多边形铺满地面,既不留下一丝空白,又不相互重叠。即无缝隙,不重叠。 那么,当用形状、大小完全相同的一种正多边形铺设地面时,在满足什么条件下,才能使拼成的平面无缝隙,不重叠呢?探索新知
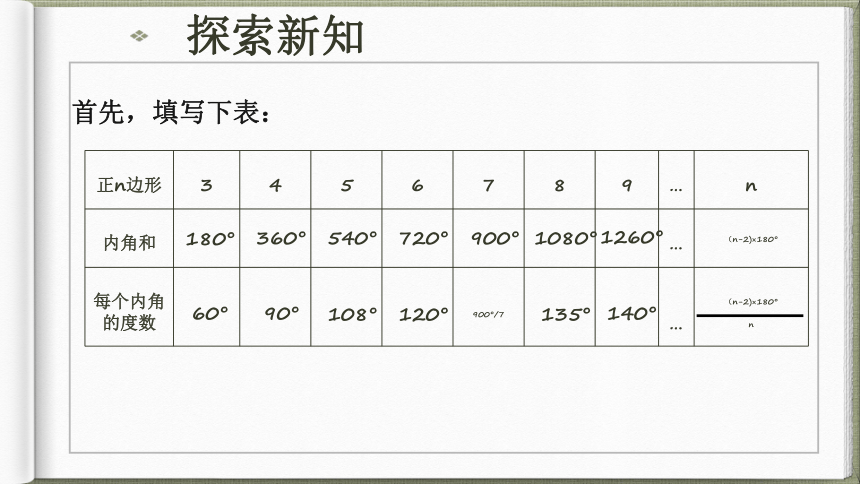
首先,填写下表:180°360°540°720°900°1080°1260°(n-2)×180°60°90°108°120°900°/7135°140°n(n-2)×180°观察探索
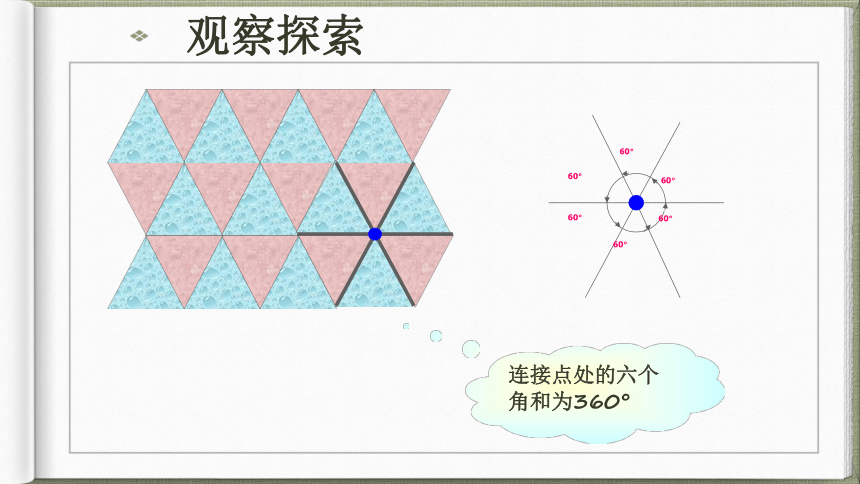
60°60°60°60°60°60°连接点处的六个角和为360°观察探索
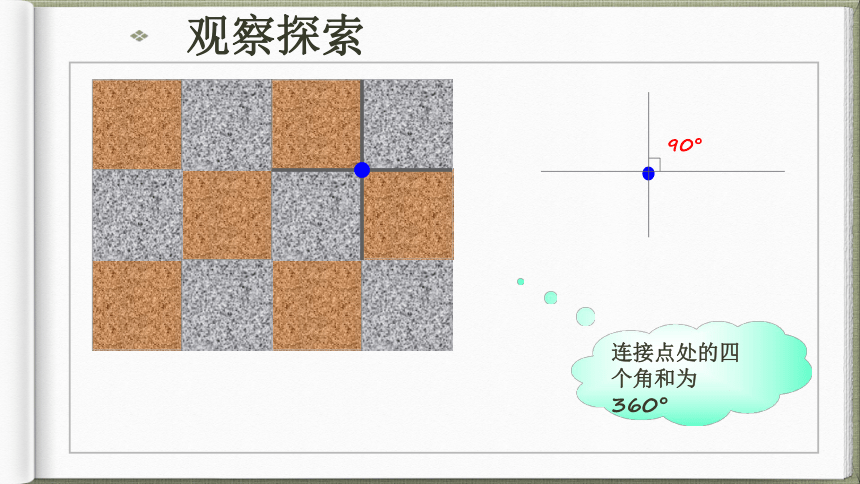
90°连接点处的四个角和为360°观察探索
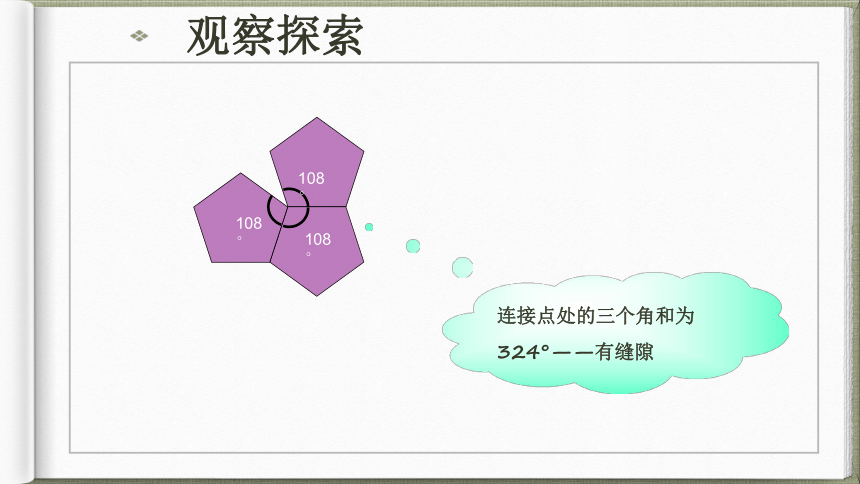
连接点处的三个角和为324°——有缝隙108°108°108°观察探索
连接点处的三个角和为360°探索新知1.现在你能概括出正多边形铺设地面的规律吗?
使用大小、形状相同的一种正多边形,当围绕一点拼在一起的几个内角和加在一起恰好组成一个周角( 360°)时,就能铺满地面。也就是说,这种正多边形的一个内角的整数倍是360°2.当只用一种正多边形铺设地面时,都有哪些种正多边形可以铺满地面呢?180°360°540°720°900°1080°1260°(n-2)×180°60°90°108°120°900°/7135°140°n(n-2)×180°只用一种正多边形铺设地面时,只有正三边形、正四边形、正六边形能够满足无缝隙、不重叠。且需要的正多边形个数为:360°÷内角的度数概括结论
只用一种大小、形状的相同的正多边形铺设地面时:关键要看:这种正多边形的一个内角的倍数是否是360°,在正多边形里,正三角形的每个内角都是60°,正四边形的每个内角都是90°,正六边形的每个内角都是120°,这三种多边形的一个内角的倍数都是360°,而其他的正多边形的每个内角的倍数都不是360°,所以说:在正多边形里只有正三角形、正四边形、正六边形可以铺满地板,而其他的正多边形不可铺铺满地板。 如果用多种不同的正多边形铺设地面呢?观察探索1.正三角形与正方形
观察探索2.正三角形与正六边形
观察探索3.正方形与正八边形
观察探索4.三种正多边形
以图9.3.5为例,分析:正十二边形的一个内角为 ,正六边形的的一个内角为 ,正方形的一个内角为 ,三角之和为150°120°90°一个周角360°概括结论
用多种正多边形铺设地面时:围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个无缝隙,不重叠的平面图形。做一做通过观察可知,当用两种不同的正多边形铺设地面时,可以有不同的组合方式,有什么方法可以确切求出一共有几种不同的组合方式呢?
例如:用正六边形和正三角形铺设时:做一做1.商店出售下列形状的地砖:⑴正三角形⑵正方形⑶正五边形⑷正六边形,若只选购其中某一种地砖铺满地面,可供选择的地砖共有( )
A.1种 B. 2种 C. 3种 D. 4种
2.能够铺满地面的边长都相等的正多边形的组合是( )
A.正三角形和正方形 B.正方形和正六边形
C.正三角形和正十二边形 D.正三角形、正方形和正六边形
CACD谢谢同学们!
七年级数观察发现
探索新知 用正多边形能够铺设地面的实质是指什么呢?
是指用某种正多边形铺满地面,既不留下一丝空白,又不相互重叠。即无缝隙,不重叠。 那么,当用形状、大小完全相同的一种正多边形铺设地面时,在满足什么条件下,才能使拼成的平面无缝隙,不重叠呢?探索新知
首先,填写下表:180°360°540°720°900°1080°1260°(n-2)×180°60°90°108°120°900°/7135°140°n(n-2)×180°观察探索
60°60°60°60°60°60°连接点处的六个角和为360°观察探索
90°连接点处的四个角和为360°观察探索
连接点处的三个角和为324°——有缝隙108°108°108°观察探索
连接点处的三个角和为360°探索新知1.现在你能概括出正多边形铺设地面的规律吗?
使用大小、形状相同的一种正多边形,当围绕一点拼在一起的几个内角和加在一起恰好组成一个周角( 360°)时,就能铺满地面。也就是说,这种正多边形的一个内角的整数倍是360°2.当只用一种正多边形铺设地面时,都有哪些种正多边形可以铺满地面呢?180°360°540°720°900°1080°1260°(n-2)×180°60°90°108°120°900°/7135°140°n(n-2)×180°只用一种正多边形铺设地面时,只有正三边形、正四边形、正六边形能够满足无缝隙、不重叠。且需要的正多边形个数为:360°÷内角的度数概括结论
只用一种大小、形状的相同的正多边形铺设地面时:关键要看:这种正多边形的一个内角的倍数是否是360°,在正多边形里,正三角形的每个内角都是60°,正四边形的每个内角都是90°,正六边形的每个内角都是120°,这三种多边形的一个内角的倍数都是360°,而其他的正多边形的每个内角的倍数都不是360°,所以说:在正多边形里只有正三角形、正四边形、正六边形可以铺满地板,而其他的正多边形不可铺铺满地板。 如果用多种不同的正多边形铺设地面呢?观察探索1.正三角形与正方形
观察探索2.正三角形与正六边形
观察探索3.正方形与正八边形
观察探索4.三种正多边形
以图9.3.5为例,分析:正十二边形的一个内角为 ,正六边形的的一个内角为 ,正方形的一个内角为 ,三角之和为150°120°90°一个周角360°概括结论
用多种正多边形铺设地面时:围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个无缝隙,不重叠的平面图形。做一做通过观察可知,当用两种不同的正多边形铺设地面时,可以有不同的组合方式,有什么方法可以确切求出一共有几种不同的组合方式呢?
例如:用正六边形和正三角形铺设时:做一做1.商店出售下列形状的地砖:⑴正三角形⑵正方形⑶正五边形⑷正六边形,若只选购其中某一种地砖铺满地面,可供选择的地砖共有( )
A.1种 B. 2种 C. 3种 D. 4种
2.能够铺满地面的边长都相等的正多边形的组合是( )
A.正三角形和正方形 B.正方形和正六边形
C.正三角形和正十二边形 D.正三角形、正方形和正六边形
CACD谢谢同学们!
