2020版高中数学新人教B版必修5课件:第二章数列专题突破四数列求和(42张)
文档属性
| 名称 | 2020版高中数学新人教B版必修5课件:第二章数列专题突破四数列求和(42张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 00:00:00 | ||
图片预览











文档简介
课件42张PPT。专题突破四 数列求和第二章 数列学习目标XUEXIMUBIAO1.掌握分组分解求和法的使用情形和解题要点.
2.掌握奇偶并项求和法的使用情形和解题要点.
3.掌握裂项相消求和法的使用情形和解题要点.
4.进一步熟悉错位相减法.NEIRONGSUOYIN内容索引自主学习题型探究达标检测1自主学习PART ONE知识点一 分组分解求和法总结 分组分解求和的基本思路:通过分解每一项重新组合,化归为等差数列和等比数列求和.知识点二 奇偶并项求和法
思考 求和12-22+32-42+…+992-1002.答案 12-22+32-42+…+992-1002
=(12-22)+(32-42)+…+(992-1002)
=(1-2)(1+2)+(3-4)(3+4)+…+(99-100)(99+100)
=-(1+2+3+4+…+99+100)
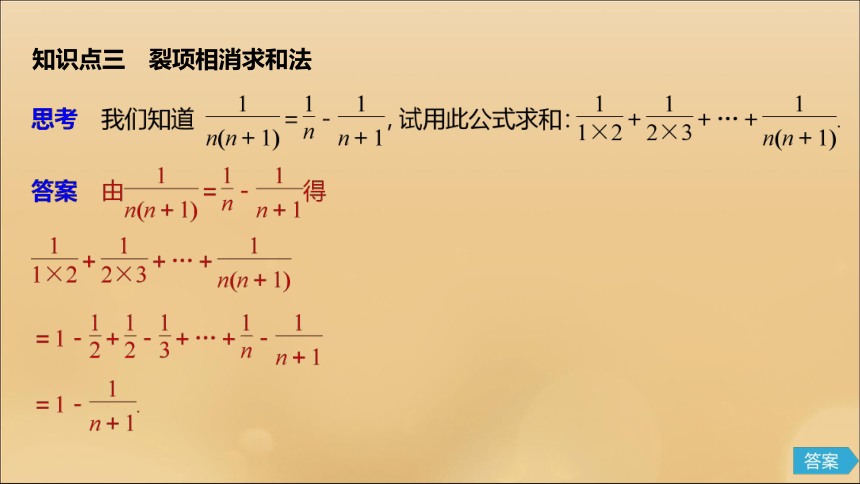
=-5 050.总结 奇偶并项求和的基本思路:有些数列单独看求和困难,但相邻项结合后会变成熟悉的等差数列、等比数列求和.但当求前n项和而n是奇数还是偶数不确定时,往往需要讨论.知识点三 裂项相消求和法总结 如果数列的项能裂成前后抵消的两项,可用裂项相消求和,此法一般先研究通项的裂法,然后仿照裂开每一项.裂项相消求和常用公式:知识点四 错位相减求和法
思考 记bn=n·2n,求数列{bn}的前n项和Sn.答案 ∵Sn=1·2+2·22+3·23+…+n·2n, ①
2Sn=1·22+2·23+3·24+…+(n-1)·2n+n·2n+1, ②
①-②,得-Sn=21+22+23+24+…+2n-n·2n+1
=-2-(n-1)·2n+1.
∴Sn=2+(n-1)·2n+1,n∈N+.总结 错位相减法主要适用于{an}是等差数列,{bn}是等比数列,求数列{anbn}的前n项和.
利用“错位相减法”时,先写出Sn与qSn的表达式,再将两式对齐作差,正确写出(1-q)Sn的表达式;(利用此法时要注意讨论公比q是否等于1).1.并项求和一定是相邻两项结合.( )
2.裂项相消一定是相邻两项裂项后产生抵消.( )思考辨析 判断正误SIKAOBIANXIPANDUANZHENGWU××2题型探究PART TWO题型一 分组分解求和解 当x≠±1时,当x=±1时,Sn=4n.反思感悟 某些数列,通过适当分组,可得出两个或几个等差数列或等比数列,进而利用等差数列或等比数列的求和公式分别求和,从而得出原数列的和.跟踪训练1 已知正项等比数列{an}中,a1+a2=6,a3+a4=24.
(1)求数列{an}的通项公式;解 设数列{an}的公比为q(q>0),∴an=a1·qn-1=2·2n-1=2n.(2)数列{bn}满足bn=log2an,求数列{an+bn}的前n项和.解 bn=log22n=n,设{an+bn}的前n项和为Sn,
则Sn=(a1+b1)+(a2+b2)+…+(an+bn)
=(a1+a2+…+an)+(b1+b2+…+bn)
=(2+22+…+2n)+(1+2+…+n)题型二 裂项相消求和以下同例2解法.引申探究反思感悟 求和前一般先对数列的通项公式变形,如果数列的通项公式可转化为f (n+1)-f(n)的形式,常采用裂项求和法.跟踪训练2 求和:题型三 奇偶并项求和例3 求和:Sn=-1+3-5+7-…+(-1)n(2n-1).解 当n为奇数时,
Sn=(-1+3)+(-5+7)+(-9+11)+…+[(-2n+5)+(2n-3)]+(-2n+1)当n为偶数时,∴Sn=(-1)nn (n∈N+).反思感悟 通项中含有(-1)n的数列求前n项和时可以考虑使用奇偶并项法,分项数为奇数和偶数分别进行求和.跟踪训练3 已知数列-1,4,-7,10,…,(-1)n·(3n-2),…,求其前n项和Sn.解 当n为偶数时,令n=2k(k∈N+),
Sn=S2k=-1+4-7+10+…+(-1)n·(3n-2)
=(-1+4)+(-7+10)+…+[(-6k+5)+(6k-2)]当n为奇数时,令n=2k-1(k∈N+),
∴Sn=S2k-1=S2k-a2k=3k-(6k-2)题型四 错位相减求和例4 (2018·佛山检测)已知数列{an}的前n项和为Sn,且满足an=3Sn-2(n∈N+).
(1)求数列{an}的通项公式;解 当n=1时,a1=3S1-2=3a1-2,解得a1=1.
当n≥2时,an=3Sn-2,an-1=3Sn-1-2,(2)求数列{nan}的前n项和Tn.两式相减得反思感悟 用错位相减要“能识别,按步走,慎化简”.跟踪训练4 已知数列{an}的通项公式为an=3n-1,在等差数列{bn}中,bn>0,且b1+b2+b3=15,又a1+b1,a2+b2,a3+b3成等比数列.
(1)求数列{anbn}的通项公式;解 ∵an=3n-1,∴a1=1,a2=3,a3=9.
∵在等差数列{bn}中,b1+b2+b3=15,∴3b2=15,则b2=5.
设等差数列{bn}的公差为d,又a1+b1,a2+b2,a3+b3成等比数列,
∴(1+5-d)(9+5+d)=64,解得d=-10或d=2.
∵bn>0,∴d=-10应舍去,∴d=2,
∴b1=3,∴bn=2n+1.
故anbn=(2n+1)·3n-1,n∈N+.解 由(1)知Tn=3×1+5×3+7×32+…+(2n-1)3n-2+(2n+1)3n-1, ①
3Tn=3×3+5×32+7×33+…+(2n-1)3n-1+(2n+1)3n, ②
①-②,得-2Tn=3×1+2×3+2×32+2×33+…+2×3n-1-(2n+1)3n
=3+2(3+32+33+…+3n-1)-(2n+1)3n
=3+2× -(2n+1)3n
=3n-(2n+1)3n
=-2n·3n.
∴Tn=n·3n,n∈N+.(2)求数列{anbn}的前n项和Tn.3达标检测PART THREE12341.数列{1+2n-1}的前n项和为_____________________.Sn=n+2n-1,n∈N+解析 ∵an=1+2n-1,12341234解析 由题意得S100=a1+a2+…+a99+a100
=(a1+a3+a5+…+a99)+(a2+a4+…+a100)
=(0+2+4+…+98)+(2+4+6+…+100)
=5 000.5 00012344.在数列{an}中,a1=1,an+1=2an+2n,n∈N+.证明 由已知an+1=2an+2n,∴bn+1-bn=1,又b1=a1=1.
∴{bn}是首项为1,公差为1的等差数列.1234(2)在(1)的条件下求数列{an}的前n项和Sn.∴an=n·2n-1.
∴Sn=1+2·21+3·22+…+n·2n-1,
两边同时乘以2得
2Sn=1·21+2·22+…+(n-1)·2n-1+n·2n,
两式相减得-Sn=1+21+22+…+2n-1-n·2n
=2n-1-n·2n=(1-n)2n-1,
∴Sn=(n-1)·2n+1.课堂小结KETANGXIAOJIE求数列的前n项和,一般有下列几种方法.
1.错位相减
适用于一个等差数列和一个等比数列对应项相乘构成的数列求和.
2.分组求和
把一个数列分成几个可以直接求和的数列.
3.裂项相消
有时把一个数列的通项公式分成两项差的形式,相加过程消去中间项,只剩有限项再求和.4.奇偶并项
当数列通项中出现(-1)n或(-1)n+1时,常常需要对n取值的奇偶性进行分类讨论.
5.倒序相加
例如,等差数列前n项和公式的推导方法.
2.掌握奇偶并项求和法的使用情形和解题要点.
3.掌握裂项相消求和法的使用情形和解题要点.
4.进一步熟悉错位相减法.NEIRONGSUOYIN内容索引自主学习题型探究达标检测1自主学习PART ONE知识点一 分组分解求和法总结 分组分解求和的基本思路:通过分解每一项重新组合,化归为等差数列和等比数列求和.知识点二 奇偶并项求和法
思考 求和12-22+32-42+…+992-1002.答案 12-22+32-42+…+992-1002
=(12-22)+(32-42)+…+(992-1002)
=(1-2)(1+2)+(3-4)(3+4)+…+(99-100)(99+100)
=-(1+2+3+4+…+99+100)
=-5 050.总结 奇偶并项求和的基本思路:有些数列单独看求和困难,但相邻项结合后会变成熟悉的等差数列、等比数列求和.但当求前n项和而n是奇数还是偶数不确定时,往往需要讨论.知识点三 裂项相消求和法总结 如果数列的项能裂成前后抵消的两项,可用裂项相消求和,此法一般先研究通项的裂法,然后仿照裂开每一项.裂项相消求和常用公式:知识点四 错位相减求和法
思考 记bn=n·2n,求数列{bn}的前n项和Sn.答案 ∵Sn=1·2+2·22+3·23+…+n·2n, ①
2Sn=1·22+2·23+3·24+…+(n-1)·2n+n·2n+1, ②
①-②,得-Sn=21+22+23+24+…+2n-n·2n+1
=-2-(n-1)·2n+1.
∴Sn=2+(n-1)·2n+1,n∈N+.总结 错位相减法主要适用于{an}是等差数列,{bn}是等比数列,求数列{anbn}的前n项和.
利用“错位相减法”时,先写出Sn与qSn的表达式,再将两式对齐作差,正确写出(1-q)Sn的表达式;(利用此法时要注意讨论公比q是否等于1).1.并项求和一定是相邻两项结合.( )
2.裂项相消一定是相邻两项裂项后产生抵消.( )思考辨析 判断正误SIKAOBIANXIPANDUANZHENGWU××2题型探究PART TWO题型一 分组分解求和解 当x≠±1时,当x=±1时,Sn=4n.反思感悟 某些数列,通过适当分组,可得出两个或几个等差数列或等比数列,进而利用等差数列或等比数列的求和公式分别求和,从而得出原数列的和.跟踪训练1 已知正项等比数列{an}中,a1+a2=6,a3+a4=24.
(1)求数列{an}的通项公式;解 设数列{an}的公比为q(q>0),∴an=a1·qn-1=2·2n-1=2n.(2)数列{bn}满足bn=log2an,求数列{an+bn}的前n项和.解 bn=log22n=n,设{an+bn}的前n项和为Sn,
则Sn=(a1+b1)+(a2+b2)+…+(an+bn)
=(a1+a2+…+an)+(b1+b2+…+bn)
=(2+22+…+2n)+(1+2+…+n)题型二 裂项相消求和以下同例2解法.引申探究反思感悟 求和前一般先对数列的通项公式变形,如果数列的通项公式可转化为f (n+1)-f(n)的形式,常采用裂项求和法.跟踪训练2 求和:题型三 奇偶并项求和例3 求和:Sn=-1+3-5+7-…+(-1)n(2n-1).解 当n为奇数时,
Sn=(-1+3)+(-5+7)+(-9+11)+…+[(-2n+5)+(2n-3)]+(-2n+1)当n为偶数时,∴Sn=(-1)nn (n∈N+).反思感悟 通项中含有(-1)n的数列求前n项和时可以考虑使用奇偶并项法,分项数为奇数和偶数分别进行求和.跟踪训练3 已知数列-1,4,-7,10,…,(-1)n·(3n-2),…,求其前n项和Sn.解 当n为偶数时,令n=2k(k∈N+),
Sn=S2k=-1+4-7+10+…+(-1)n·(3n-2)
=(-1+4)+(-7+10)+…+[(-6k+5)+(6k-2)]当n为奇数时,令n=2k-1(k∈N+),
∴Sn=S2k-1=S2k-a2k=3k-(6k-2)题型四 错位相减求和例4 (2018·佛山检测)已知数列{an}的前n项和为Sn,且满足an=3Sn-2(n∈N+).
(1)求数列{an}的通项公式;解 当n=1时,a1=3S1-2=3a1-2,解得a1=1.
当n≥2时,an=3Sn-2,an-1=3Sn-1-2,(2)求数列{nan}的前n项和Tn.两式相减得反思感悟 用错位相减要“能识别,按步走,慎化简”.跟踪训练4 已知数列{an}的通项公式为an=3n-1,在等差数列{bn}中,bn>0,且b1+b2+b3=15,又a1+b1,a2+b2,a3+b3成等比数列.
(1)求数列{anbn}的通项公式;解 ∵an=3n-1,∴a1=1,a2=3,a3=9.
∵在等差数列{bn}中,b1+b2+b3=15,∴3b2=15,则b2=5.
设等差数列{bn}的公差为d,又a1+b1,a2+b2,a3+b3成等比数列,
∴(1+5-d)(9+5+d)=64,解得d=-10或d=2.
∵bn>0,∴d=-10应舍去,∴d=2,
∴b1=3,∴bn=2n+1.
故anbn=(2n+1)·3n-1,n∈N+.解 由(1)知Tn=3×1+5×3+7×32+…+(2n-1)3n-2+(2n+1)3n-1, ①
3Tn=3×3+5×32+7×33+…+(2n-1)3n-1+(2n+1)3n, ②
①-②,得-2Tn=3×1+2×3+2×32+2×33+…+2×3n-1-(2n+1)3n
=3+2(3+32+33+…+3n-1)-(2n+1)3n
=3+2× -(2n+1)3n
=3n-(2n+1)3n
=-2n·3n.
∴Tn=n·3n,n∈N+.(2)求数列{anbn}的前n项和Tn.3达标检测PART THREE12341.数列{1+2n-1}的前n项和为_____________________.Sn=n+2n-1,n∈N+解析 ∵an=1+2n-1,12341234解析 由题意得S100=a1+a2+…+a99+a100
=(a1+a3+a5+…+a99)+(a2+a4+…+a100)
=(0+2+4+…+98)+(2+4+6+…+100)
=5 000.5 00012344.在数列{an}中,a1=1,an+1=2an+2n,n∈N+.证明 由已知an+1=2an+2n,∴bn+1-bn=1,又b1=a1=1.
∴{bn}是首项为1,公差为1的等差数列.1234(2)在(1)的条件下求数列{an}的前n项和Sn.∴an=n·2n-1.
∴Sn=1+2·21+3·22+…+n·2n-1,
两边同时乘以2得
2Sn=1·21+2·22+…+(n-1)·2n-1+n·2n,
两式相减得-Sn=1+21+22+…+2n-1-n·2n
=2n-1-n·2n=(1-n)2n-1,
∴Sn=(n-1)·2n+1.课堂小结KETANGXIAOJIE求数列的前n项和,一般有下列几种方法.
1.错位相减
适用于一个等差数列和一个等比数列对应项相乘构成的数列求和.
2.分组求和
把一个数列分成几个可以直接求和的数列.
3.裂项相消
有时把一个数列的通项公式分成两项差的形式,相加过程消去中间项,只剩有限项再求和.4.奇偶并项
当数列通项中出现(-1)n或(-1)n+1时,常常需要对n取值的奇偶性进行分类讨论.
5.倒序相加
例如,等差数列前n项和公式的推导方法.
