10.1.2 抽对称的再认识 课件(24张PPT)
文档属性
| 名称 | 10.1.2 抽对称的再认识 课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 178.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 10:08:41 | ||
图片预览


文档简介
课件24张PPT。10.1.2 轴对称的再认识课程引入什么是轴对称图形?线段是轴对称图形吗?角是轴对称图形吗?它们都有那些性质那?一、线段的垂直平分线:线段是不是轴对称图形?AB探究学习要回答此问题,就必须弄清楚什么是轴对称图形。还记得吗?就是:把一个图形沿某条直线
对折,对折的两部分是
完全重合的,这样的图
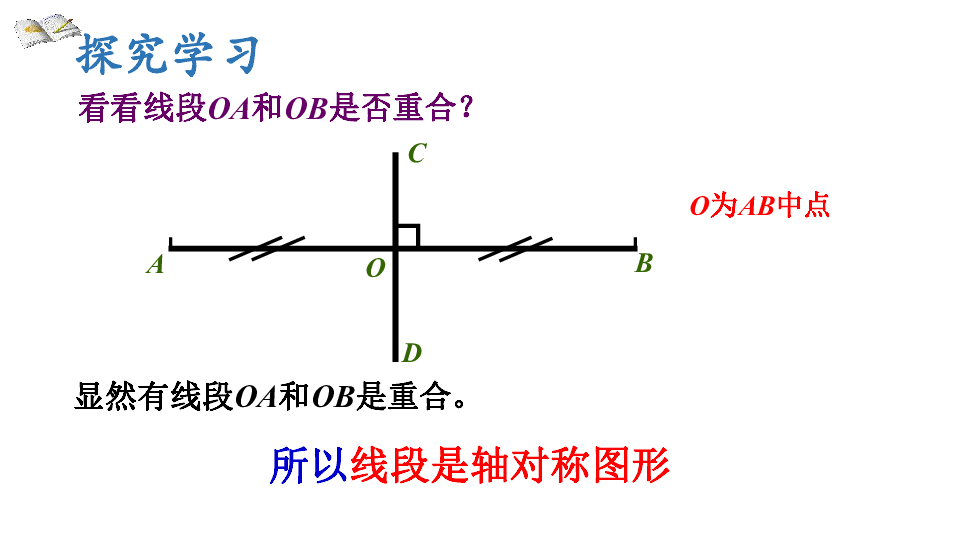
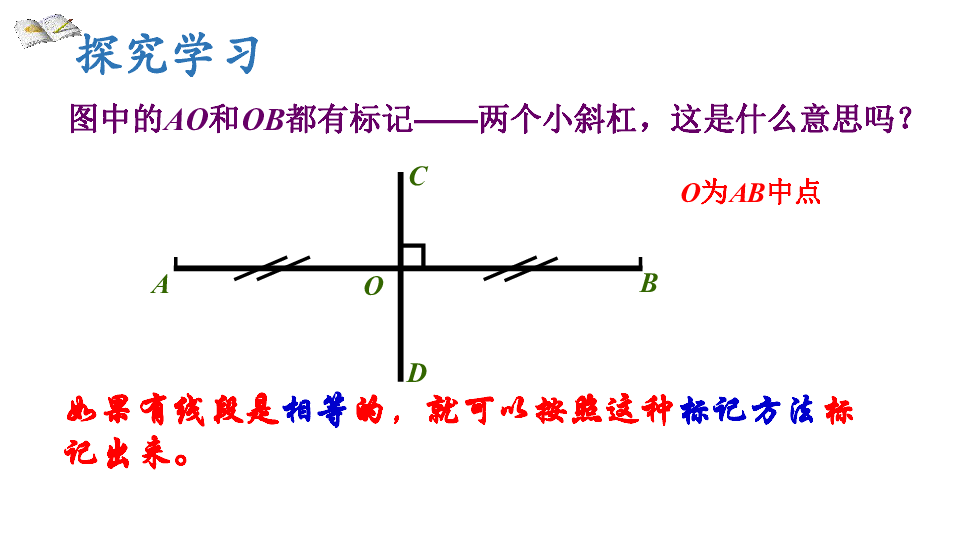
称为轴对称图形。看看线段OA和OB是否重合?显然有线段OA和OB是重合。 ABOCDO为AB中点所以线段是轴对称图形探究学习图中的AO和OB都有标记——两个小斜杠,这是什么意思吗?ABOCDO为AB中点如果有线段是相等的,就可以按照这种标记方法标记出来。 探究学习垂直平分线定义:
根据刚才的实验,我们知道线段AB是轴对称图形。直线CD是它的对称轴。直线CD既垂直于线段AB,又平分线AB。定义:垂直并且平分一条线段的直线称为这条线段垂直平分线,又叫中垂线。探究学习ABOCDO为AB中点线段MA和MB会重合吗?M分析:由于A点和B点重合,M点是同一点(公共点),所以线段MA和MB会重合。结论:线段的垂直平分线上的点到这条线段两个端点的距离相等。这是线段垂直平分线的重要性质。课程引入1、既垂直又平分线段的直线叫做这条线段的垂直平分线。
2、线段的垂直平分线上的点到这条线段两个端点的距离相等。 探究学习补充知识:直线也是轴对称图形,有无数条对称轴
射线也是轴对称图形,对称轴是自身所在的直线。△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D;BE=6,求△BCE的周长。∵ED是BC的垂直平分线(已知)
∴EC=EB=6
(线段的垂直平分线上的点到这条线段
两个端点的距离相等)
∴△BCE的周长=BC+CE+EB=10+6+6=22
答:△BCE的周长为22。课堂精讲 解: 例1: 如下图,草原上两个居民点A、B在河流的同旁.一汽车从点A出发到B,途中需要到河边加水.汽车在哪一点加水,可使行驶的路程最短?在图中作出该处,并说明理由;在图上画出这点。ABA′河MCDE 例2:课堂精讲已知:直线CD和CD同侧两点A、B.
求作:CD上一点M,使AM+BM最小.M′AB 在CD上任取一点M′,连结AM、AM′、A′M′、BM′
直线CD是A、A′的对称轴,M、M′在CD上,
∴AM=A′M,AM′=A′M′
∴AM+BM=A′M+BM=A′B
在△A′M′B中
∵A′M′+BM′>A′B
(三角形两边之和大于第三边)
∴A′M′+BM′>AM+BM
即AM+BM最小.A′河MCDE课堂精讲 证明:作法:①作点A关于CD的对称点A′,
②连结A′B交CD于点M,则点M即为所求的点. 解:一、填空题:
1.到线段的两个端点距离相等的点有 个.
2.平分一条已知线段的直线有 条;垂直平分一条已知线段的直线有 条.
3.一条已知线段的对称轴有 条.
4.成轴对称的两个多边形,一个周长为15 cm,则另一个多边形的周长为 cm.无数无数12二、判断题(对的在题后的括号内打“√”,错的打“×”)
5.线段的垂直平分线上存在到这线段两端点距离不相等的点( )
6.有一公共端点的两条相等线段的图形是轴对称图形 ( )
7.角是轴对称图形,对称轴是角平分线 ( )×√×15课堂反馈ABC三、解答题:
如图,A、B、C三点表示三个镇的地理位置,随着乡镇外资、集体、个体工业的发展需要,现三镇联合建造一个变电所,要求变电所到三镇的距离相等,请你作出变电所的位置(用点P表示)作法:
1、分别连接AB、BC。
2、分别作线段AB、BC的垂直平分线
两直线交于点P。
则点P为所求的变电所的位置。P能想通为什么吗?课堂精讲探究学习角是不是轴对称图形?ABO1.角平分线的性质 试验:按以下方法试验,使同学认识角是轴对称图形。
在半透明的纸上画∠AOB,对折,使角的两条边完全重合,然后用直尺画出折痕OM。
从上面试验可以看出,角是轴对称图形,对称轴是它的角平分线所在的直线。ABOP结论:角是轴对称图形探究学习2.角平分线上的点到角两边的距离探索 在以上试验的基础上,同学们在射线OM上任取一点P,过P点分别作OA和OB的垂线PC和PD,而后沿着OM折叠,观察PC和 PD是否重合?再取一点,按上述同样的方法试验。关系:PC与PD是能够互相重合的.
即PC=PD 角平分线上的点到角两边的距离相等.探究学习一、判断题(对的打“√”,错的打“×”)
(1)角平分线上存在到这个角的两边距离不相等的点( )
(2)到一个角两边的距离相等的点在这个角的平分线上( )
(3)角是轴对称图形,对称轴是角平分线 ( )×√×二、如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30, BD:CD=3:2,则点D到AB 的距离是( )
A.18 B.12 C.15 D.不能确定 B课堂反馈课堂反馈三、如图所示,在△ABC中,∠C= 90°,BD是角平分线,交AC于点D,DE⊥AB,垂足为点E,AD=3DE。AD和3DC是什么关系?为什么?解:∵ ∠C= 90°,BD是角平分线, DE⊥AB
∴ DE=DC(角平分线上的点到角两边的距离相等)
∵ AD=3DE
∴ AD=3DC四、如图,在直线l上找一点P,使P到射线AB和AC的距离相等. P作法:作∠BAC的平分线,交直线l 于点P。则点P为所求作的点。课堂反馈课堂反馈五、如图,BD平分∠ABC,AE⊥BC,垂足为E,交BD于P点,PE =3 cm,求 P点到直线AB的距离。 解:过点P作PF⊥AB于点F
∵ BD平分∠ABC ,PE⊥BC,PF⊥AB
∴ PF=PE=3 cm
(角平分线上的点到角两边的距离相等)
答:点P到直线AB的距离为3 cm。4、角平分线上的点到角两边的距离相等。 3、角是轴对称图形,对称轴是角平分线所在的直线;
运用角平分线性质可以说明两条线段等。课堂小结1、既垂直又平分线段的直线叫做这条线段的垂直平分线。
2、线段的垂直平分线上的点到这条线段两个端点的距离相等。 常见的轴对称图形课堂小结巩固提升1.如图:已知△ABC中,∠C=90°,AB的垂直平分线交BC于点D,如果∠CAD=20°,则∠B=?????? 。2.在△ABC中,找一点P,使点P到△ABC三边的距离相等。3.如右图,AD平分∠BAC,∠C=90°,DE⊥AB,那么
(1)DE与DC相等吗?为什么?
(2)AE与AC相等吗?如图,某镇的两个村A、B在长江的南岸l的南面,镇政府为民办实事,决定为两村通自来水,应在南岸l上何处建水厂,才能使水厂P到两村的水管的长度相等? ABP作法:
1、连接AB。
2、作线段AB的垂直平分线
交直线l于点P
则点P为所求的水厂的位置。作业
对折,对折的两部分是
完全重合的,这样的图
称为轴对称图形。看看线段OA和OB是否重合?显然有线段OA和OB是重合。 ABOCDO为AB中点所以线段是轴对称图形探究学习图中的AO和OB都有标记——两个小斜杠,这是什么意思吗?ABOCDO为AB中点如果有线段是相等的,就可以按照这种标记方法标记出来。 探究学习垂直平分线定义:
根据刚才的实验,我们知道线段AB是轴对称图形。直线CD是它的对称轴。直线CD既垂直于线段AB,又平分线AB。定义:垂直并且平分一条线段的直线称为这条线段垂直平分线,又叫中垂线。探究学习ABOCDO为AB中点线段MA和MB会重合吗?M分析:由于A点和B点重合,M点是同一点(公共点),所以线段MA和MB会重合。结论:线段的垂直平分线上的点到这条线段两个端点的距离相等。这是线段垂直平分线的重要性质。课程引入1、既垂直又平分线段的直线叫做这条线段的垂直平分线。
2、线段的垂直平分线上的点到这条线段两个端点的距离相等。 探究学习补充知识:直线也是轴对称图形,有无数条对称轴
射线也是轴对称图形,对称轴是自身所在的直线。△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D;BE=6,求△BCE的周长。∵ED是BC的垂直平分线(已知)
∴EC=EB=6
(线段的垂直平分线上的点到这条线段
两个端点的距离相等)
∴△BCE的周长=BC+CE+EB=10+6+6=22
答:△BCE的周长为22。课堂精讲 解: 例1: 如下图,草原上两个居民点A、B在河流的同旁.一汽车从点A出发到B,途中需要到河边加水.汽车在哪一点加水,可使行驶的路程最短?在图中作出该处,并说明理由;在图上画出这点。ABA′河MCDE 例2:课堂精讲已知:直线CD和CD同侧两点A、B.
求作:CD上一点M,使AM+BM最小.M′AB 在CD上任取一点M′,连结AM、AM′、A′M′、BM′
直线CD是A、A′的对称轴,M、M′在CD上,
∴AM=A′M,AM′=A′M′
∴AM+BM=A′M+BM=A′B
在△A′M′B中
∵A′M′+BM′>A′B
(三角形两边之和大于第三边)
∴A′M′+BM′>AM+BM
即AM+BM最小.A′河MCDE课堂精讲 证明:作法:①作点A关于CD的对称点A′,
②连结A′B交CD于点M,则点M即为所求的点. 解:一、填空题:
1.到线段的两个端点距离相等的点有 个.
2.平分一条已知线段的直线有 条;垂直平分一条已知线段的直线有 条.
3.一条已知线段的对称轴有 条.
4.成轴对称的两个多边形,一个周长为15 cm,则另一个多边形的周长为 cm.无数无数12二、判断题(对的在题后的括号内打“√”,错的打“×”)
5.线段的垂直平分线上存在到这线段两端点距离不相等的点( )
6.有一公共端点的两条相等线段的图形是轴对称图形 ( )
7.角是轴对称图形,对称轴是角平分线 ( )×√×15课堂反馈ABC三、解答题:
如图,A、B、C三点表示三个镇的地理位置,随着乡镇外资、集体、个体工业的发展需要,现三镇联合建造一个变电所,要求变电所到三镇的距离相等,请你作出变电所的位置(用点P表示)作法:
1、分别连接AB、BC。
2、分别作线段AB、BC的垂直平分线
两直线交于点P。
则点P为所求的变电所的位置。P能想通为什么吗?课堂精讲探究学习角是不是轴对称图形?ABO1.角平分线的性质 试验:按以下方法试验,使同学认识角是轴对称图形。
在半透明的纸上画∠AOB,对折,使角的两条边完全重合,然后用直尺画出折痕OM。
从上面试验可以看出,角是轴对称图形,对称轴是它的角平分线所在的直线。ABOP结论:角是轴对称图形探究学习2.角平分线上的点到角两边的距离探索 在以上试验的基础上,同学们在射线OM上任取一点P,过P点分别作OA和OB的垂线PC和PD,而后沿着OM折叠,观察PC和 PD是否重合?再取一点,按上述同样的方法试验。关系:PC与PD是能够互相重合的.
即PC=PD 角平分线上的点到角两边的距离相等.探究学习一、判断题(对的打“√”,错的打“×”)
(1)角平分线上存在到这个角的两边距离不相等的点( )
(2)到一个角两边的距离相等的点在这个角的平分线上( )
(3)角是轴对称图形,对称轴是角平分线 ( )×√×二、如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30, BD:CD=3:2,则点D到AB 的距离是( )
A.18 B.12 C.15 D.不能确定 B课堂反馈课堂反馈三、如图所示,在△ABC中,∠C= 90°,BD是角平分线,交AC于点D,DE⊥AB,垂足为点E,AD=3DE。AD和3DC是什么关系?为什么?解:∵ ∠C= 90°,BD是角平分线, DE⊥AB
∴ DE=DC(角平分线上的点到角两边的距离相等)
∵ AD=3DE
∴ AD=3DC四、如图,在直线l上找一点P,使P到射线AB和AC的距离相等. P作法:作∠BAC的平分线,交直线l 于点P。则点P为所求作的点。课堂反馈课堂反馈五、如图,BD平分∠ABC,AE⊥BC,垂足为E,交BD于P点,PE =3 cm,求 P点到直线AB的距离。 解:过点P作PF⊥AB于点F
∵ BD平分∠ABC ,PE⊥BC,PF⊥AB
∴ PF=PE=3 cm
(角平分线上的点到角两边的距离相等)
答:点P到直线AB的距离为3 cm。4、角平分线上的点到角两边的距离相等。 3、角是轴对称图形,对称轴是角平分线所在的直线;
运用角平分线性质可以说明两条线段等。课堂小结1、既垂直又平分线段的直线叫做这条线段的垂直平分线。
2、线段的垂直平分线上的点到这条线段两个端点的距离相等。 常见的轴对称图形课堂小结巩固提升1.如图:已知△ABC中,∠C=90°,AB的垂直平分线交BC于点D,如果∠CAD=20°,则∠B=?????? 。2.在△ABC中,找一点P,使点P到△ABC三边的距离相等。3.如右图,AD平分∠BAC,∠C=90°,DE⊥AB,那么
(1)DE与DC相等吗?为什么?
(2)AE与AC相等吗?如图,某镇的两个村A、B在长江的南岸l的南面,镇政府为民办实事,决定为两村通自来水,应在南岸l上何处建水厂,才能使水厂P到两村的水管的长度相等? ABP作法:
1、连接AB。
2、作线段AB的垂直平分线
交直线l于点P
则点P为所求的水厂的位置。作业
