2020版高中数学新人教B版必修5课件:第三章不等式3.1.2不等式的性质(33张)
文档属性
| 名称 | 2020版高中数学新人教B版必修5课件:第三章不等式3.1.2不等式的性质(33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 00:00:00 | ||
图片预览











文档简介
课件33张PPT。3.1.2 不等式的性质第三章 §3.1 不等关系与不等式学习目标XUEXIMUBIAO1.理解并掌握不等式的性质.
2.能够利用不等式的性质进行数或式的大小比较.
3.会证明一些简单的不等式.NEIRONGSUOYIN内容索引自主学习题型探究达标检测1自主学习PART ONE知识点一 不等式的基本性质思考 试用作差法证明a>b,b>c?a>c.答案 a>b,b>c?a-b>0,b-c>0?a-b+b-c>0?a-c>0?a>c.总结 不等式性质:<>>>>><>>>知识点二 不等式性质的注意事项思考1 在性质4的推论1中,若把a,b,c,d为正数的条件去掉,即a>b,c>d,能推出ac>bd吗?若不能,试举出反例.答案 不能,例如1>-2,2>-3,但1×2=2<(-2)×(-3).思考2 在性质3的推论2中,能把“?”改为“?”吗?为什么?答案 不能,因为由a+c>b+d,不能推出a>b,c>d,例如1+100>2+3,但显然1<2.总结 (1)注意不等式成立的条件,不要弱化条件,尤其是不要想当然随意捏造性质.
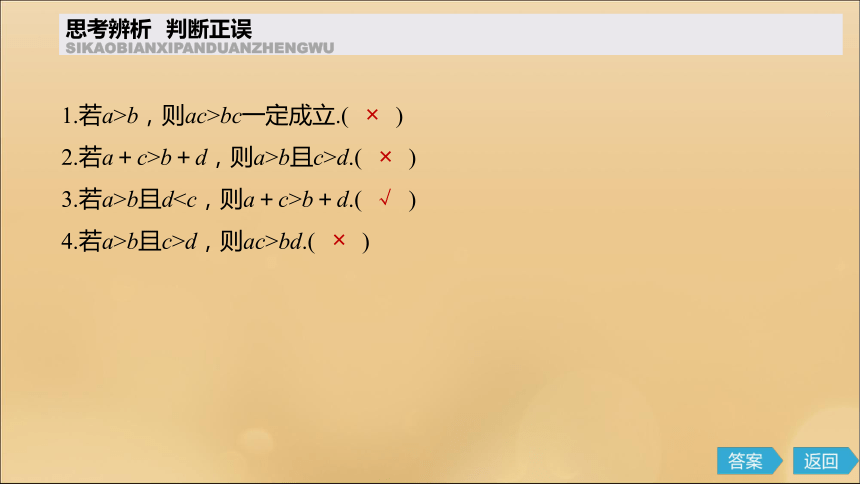
(2)注意不等式性质的单向性或双向性,即每条性质是否具有可逆性,只有a>b?b<a,a>b?a+c>b+c,a>b?ac>bc(c>0)是可以逆推的,其余几条性质不可逆推.1.若a>b,则ac>bc一定成立.( )
2.若a+c>b+d,则a>b且c>d.( )
3.若a>b且db+d.( )
4.若a>b且c>d,则ac>bd.( )思考辨析 判断正误SIKAOBIANXIPANDUANZHENGWU×√××2题型探究PART TWO题型一 不等式性质的证明例1 若a>b,c>0,求证:ac>bc.证明 ac-bc=(a-b)c.
∵a>b,∴a-b>0.
又c>0,∴(a-b)c>0,即ac-bc>0,
∴ac>bc.反思感悟 对任意两个实数a,b有a-b>0?a>b;a-b=0?a=b;a-b<0?a<b.这是比较两个实数大小的依据,也是证明不等式的基础.数学是个讲究逻辑的学科,不能以理解代替证明.跟踪训练1 (1)若ac2>bc2,求证:a>b;解 ∵ac2>bc2,
∴ac2-bc2>0,即(a-b)c2>0.
若c2=0,则ac2=bc2与条件矛盾.
∴c2>0,
∴a-b>0,即a>b.(2)由a>b能推出ac2>bc2吗?解 不能.当c=0时,ac2=bc2.例2 判断下列命题的真假:
(1)若a>b,则ac因而判断ac与bc的大小缺乏依据.故该命题为假命题.(2)若aab>b2;所以a2>ab>b2,故该命题为真命题.题型二 不等式性质的应用多维探究反思感悟 要判断命题是真命题,应说明理由或进行证明,推理过程应紧扣有关定理、性质等,应熟练掌握不等式的性质及其推论的条件和结论,若判断命题是假命题只需举一反例即可.跟踪训练2 下列命题中正确的个数是
①若a>b,b≠0,则>1;
②若a>b,且a+c>b+d,则c>d;
③若a>b,且ac>bd,则c>d.
A.0 B.1 C.2 D.3解析 ①若a=2,b=-1,则不符合题意;
②取a=10,b=2,c=1,d=3,虽然满足a>b且a+c>b+d,但不满足c>d,故错;
③当a=-2,b=-3时,取c=-1,d=2,则c>d不成立.√命题角度2 利用不等式性质证明简单不等式证明 ∵c-d>0,
∵a>b>0,反思感悟 利用不等式性质证明简单的不等式的实质就是根据性质把不等式进行变形,要注意不等式性质成立的条件,如果不能直接由不等式性质得到,可先分析需要证明的不等式的结构,利用不等式性质进行转化.证明 ∵c-d>0.
又a>b>0,∴-ac>-bd>0,∴ac∴-10<2a+b<19.
又∵-3<-b<-2,∴-9如对②③,设a=-9,b=1,
对④,设a=-1,b=2即可.A.0 B.1 C.2 D.3√解析 由题意可令a=1,b=-1,此时①不对,②不对,1234A.0 B.1 C.2 D.3√1234√解析 ∵ab>0,即-bc>-ad,即bc2.不等式的性质是解(证)不等式的基础,要依据不等式的性质进行推导,不能自己“制造”性质运算.
2.能够利用不等式的性质进行数或式的大小比较.
3.会证明一些简单的不等式.NEIRONGSUOYIN内容索引自主学习题型探究达标检测1自主学习PART ONE知识点一 不等式的基本性质思考 试用作差法证明a>b,b>c?a>c.答案 a>b,b>c?a-b>0,b-c>0?a-b+b-c>0?a-c>0?a>c.总结 不等式性质:<>>>>><>>>知识点二 不等式性质的注意事项思考1 在性质4的推论1中,若把a,b,c,d为正数的条件去掉,即a>b,c>d,能推出ac>bd吗?若不能,试举出反例.答案 不能,例如1>-2,2>-3,但1×2=2<(-2)×(-3).思考2 在性质3的推论2中,能把“?”改为“?”吗?为什么?答案 不能,因为由a+c>b+d,不能推出a>b,c>d,例如1+100>2+3,但显然1<2.总结 (1)注意不等式成立的条件,不要弱化条件,尤其是不要想当然随意捏造性质.
(2)注意不等式性质的单向性或双向性,即每条性质是否具有可逆性,只有a>b?b<a,a>b?a+c>b+c,a>b?ac>bc(c>0)是可以逆推的,其余几条性质不可逆推.1.若a>b,则ac>bc一定成立.( )
2.若a+c>b+d,则a>b且c>d.( )
3.若a>b且d
4.若a>b且c>d,则ac>bd.( )思考辨析 判断正误SIKAOBIANXIPANDUANZHENGWU×√××2题型探究PART TWO题型一 不等式性质的证明例1 若a>b,c>0,求证:ac>bc.证明 ac-bc=(a-b)c.
∵a>b,∴a-b>0.
又c>0,∴(a-b)c>0,即ac-bc>0,
∴ac>bc.反思感悟 对任意两个实数a,b有a-b>0?a>b;a-b=0?a=b;a-b<0?a<b.这是比较两个实数大小的依据,也是证明不等式的基础.数学是个讲究逻辑的学科,不能以理解代替证明.跟踪训练1 (1)若ac2>bc2,求证:a>b;解 ∵ac2>bc2,
∴ac2-bc2>0,即(a-b)c2>0.
若c2=0,则ac2=bc2与条件矛盾.
∴c2>0,
∴a-b>0,即a>b.(2)由a>b能推出ac2>bc2吗?解 不能.当c=0时,ac2=bc2.例2 判断下列命题的真假:
(1)若a>b,则ac
①若a>b,b≠0,则>1;
②若a>b,且a+c>b+d,则c>d;
③若a>b,且ac>bd,则c>d.
A.0 B.1 C.2 D.3解析 ①若a=2,b=-1,则不符合题意;
②取a=10,b=2,c=1,d=3,虽然满足a>b且a+c>b+d,但不满足c>d,故错;
③当a=-2,b=-3时,取c=-1,d=2,则c>d不成立.√命题角度2 利用不等式性质证明简单不等式证明 ∵c
∵a>b>0,反思感悟 利用不等式性质证明简单的不等式的实质就是根据性质把不等式进行变形,要注意不等式性质成立的条件,如果不能直接由不等式性质得到,可先分析需要证明的不等式的结构,利用不等式性质进行转化.证明 ∵c
又a>b>0,∴-ac>-bd>0,∴ac
又∵-3<-b<-2,∴-9
对④,设a=-1,b=2即可.A.0 B.1 C.2 D.3√解析 由题意可令a=1,b=-1,此时①不对,②不对,1234A.0 B.1 C.2 D.3√1234√解析 ∵ab>0,即-bc>-ad,即bc
