2020版高中数学新人教B版必修5课件:第三章不等式章末复习(40张)
文档属性
| 名称 | 2020版高中数学新人教B版必修5课件:第三章不等式章末复习(40张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 10:08:32 | ||
图片预览











文档简介
课件40张PPT。章末复习第三章 不等式学习目标XUEXIMUBIAO1.整合知识结构,进一步巩固、深化所学知识.
2.能熟练利用不等式的性质比较大小、变形不等式、证明不等式.
3.会用均值不等式证明不等式,求解最值问题.
4.体会“三个二次”之间的内在联系在解决问题中的作用.
5.能熟练地运用图解法解决线性规划问题.NEIRONGSUOYIN内容索引知识梳理题型探究达标检测1知识梳理PART ONE知识梳理1.不等式的性质ZHISHISHULI<>>>><>>>>2.均值不等式
利用均值不等式证明不等式和求最值的区别
(1)利用均值不等式证明不等式,只需关注不等式成立的条件.
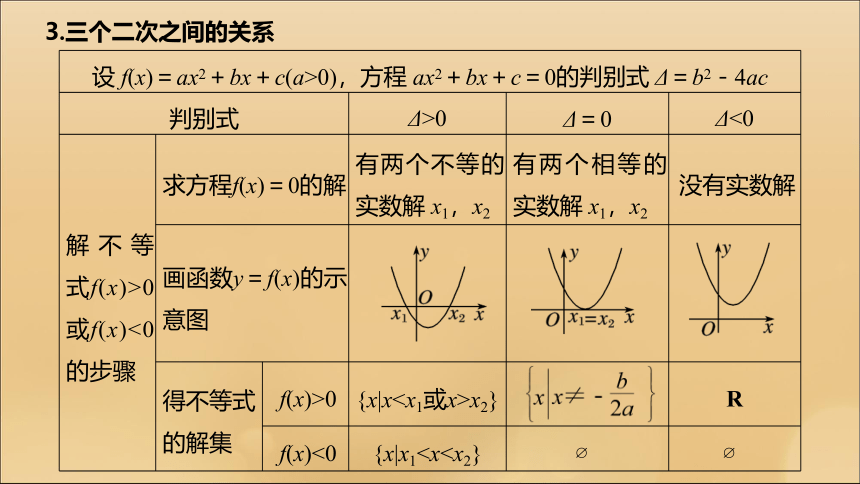
(2)利用均值不等式求最值,需要同时关注三个限制条件:一正;二定;三相等.3.三个二次之间的关系4.线性规划问题求解步骤
(1)把问题要求转化为约束条件;
(2)根据约束条件作出可行域;
(3)对目标函数变形并解释其几何意义;
(4)移动目标函数寻找最优解;
(5)解相关方程组求出最优解.2题型探究PART TWO题型一 利用均值不等式求最值4解析 y=a1-x(a>0,a≠1)的图象恒过定点 A(1,1),
∵点A在直线mx+ny-1=0上,∴m+n=1,反思感悟 当所给附加条件是一个等式时,常见的用法有两个:一个是用这个等式消元,化为命题角度1的类型;一个是直接利用该等式代入,或构造定值.题型二 “三个二次”之间的关系-14∴a+b=-14.反思感悟 (1)“三个二次”之间要选择一个运算简单的方向进行转化.
(2)用不等式组来刻画两根的位置体现了数形结合的思想.跟踪训练2 设不等式x2-2ax+a+2≤0的解集为M,如果M?[1,4],求实数a的取值范围.解 M?[1,4]有两种情况:
其一是M=?,此时Δ<0;其二是M≠?,此时Δ=0或Δ>0,下面分三种情况计算a的取值范围.
设f(x)=x2-2ax+a+2,
对方程x2-2ax+a+2=0,
有Δ=(-2a)2-4(a+2)=4(a2-a-2),
①当Δ<0时,-1②当Δ=0时,a=-1或a=2.
当a=-1时,M={-1} ? [1,4],不满足题意;
当a=2时,M={2}?[1,4],满足题意.③当Δ>0时,a<-1或a>2.
设方程f(x)=0的两根为x1,x2,且x1那么M=[x1,x2],M?[1,4]?1≤x10(a∈R).解 原不等式可化为(x-a)(x-a2)>0.
当a<0时,aa2};
当a=0时,a2=a,原不等式的解集为{x|x≠0,x∈R};
当0a};
当a=1时,a2=a,原不等式的解集为{x|x≠1,x∈R};
当a>1时,aa2};
综上所述,当a<0或a>1时,原不等式的解集为{x|xa2};
当0a};
当a=1时,原不等式的解集为{x|x≠1,x∈R};
当a=0时,原不等式的解集为{x|x≠0,x∈R}.反思感悟 对于含参数的一元二次不等式,若二次项系数为常数,则可先考虑分解因式,再对参数进行讨论;若不易分解因式,则可对判别式分类讨论,分类要不重不漏.跟踪训练3 已知常数a∈R,解关于x的不等式ax2-2x+a<0.解 (1)若a=0,则原不等式为-2x<0,故解集为{x|x>0}.
(2)若a>0,Δ=4-4a2.
①当Δ>0,即0③当Δ<0,即a>1时,原不等式的解集为?.(3)若a<0,Δ=4-4a2.②当Δ=0,即a=-1时,原不等式化为(x+1)2>0,
∴当a=-1时,原不等式的解集为{x|x∈R且x≠-1}.
③当Δ<0,即a<-1时,原不等式的解集为R.
综上所述,当a≥1时,原不等式的解集为?;当a=0时,原不等式的解集为{x|x>0};当a=-1时,原不等式的解集为{x|x∈R且x≠-1};
当a<-1时,原不等式的解集为R.题型四 线性规划问题解 如图,阴影部分(含边界)为不等式组所表示的可行域.设l0:2x+y=0,l:2x+y=z,则z的几何意义是直线y=-2x+z在y轴上的截距,显然,直线越往上移动,对应在y轴上的截距越大,即z越大;直线越往下移动,对应在y轴上的截距越小,即z越小.
上下平移直线l0,可得当l0过点A(5,2)时,zmax=2×5+2=12;
当l0过点B(1,1)时,zmin=2×1+1=3.反思感悟 (1)因为最优解与可行域的边界斜率有关,所以画可行域要尽可能精确.
(2)线性目标函数的最值与纵截距不一定是增函数关系,所以要关注纵截距越大,z越大还是越小.跟踪训练4 某人承揽一项业务,需做文字标牌4个,绘画标牌5个.现有两种规格的原料,甲种规格每张3 m2,可做文字标牌1个,绘画标牌2个;乙种规格每张2 m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张才能使得总用料面积最小.解 设需要甲种原料x张,乙种原料y张,
则可做文字标牌(x+2y)个,绘画标牌(2x+y)个,所用原料的总面积为z=3x+2y,
作出可行域如图阴影部分(含边界)所示.在一组平行直线3x+2y=z中,
经过可行域内的点A时,z取得最小值,
直线2x+y=5和直线x+2y=4的交点为A(2,1),
即最优解为(2,1).
所以使用甲种规格原料2张,乙种规格原料1张,可使总的用料面积最小.3达标检测PART THREE12341.(2018·全国Ⅰ)已知集合A={x|x2-x-2>0},则?RA等于
A.{x|-1B.{x|-1≤x≤2}
C.{x|x<-1}∪{x|x>2}
D.{x|x≤-1}∪{x|x≥2}√解析 方法一 A={x|(x-2)(x+1)>0}={x|x<-1或x>2},
所以?RA={x|-1≤x≤2},故选B.
方法二 因为A={x|x2-x-2>0},
所以?RA={x|x2-x-2≤0}={x|-1≤x≤2},故选B.5取得最大值时的最优解有无穷多个,则实数m的值为1234√解析 作出不等式组表示的平面区域如图阴影部分(包含边界)所示,由图可知当直线y=mx-z(m≠0)与直线2x-2y+1=0重合,即m=1时,目标函数z=mx-y取最大值的最优解有无穷多个,故选A.51234A.-18 B.8 C.-13 D.1√512344.若不等式4(a-2)x2+2(a-2)x-1<0对一切x∈R恒成立,则a的取值范围
是_______.(-2,2]解析 不等式4(a-2)x2+2(a-2)x-1<0,当a-2=0,即a=2时,不等式恒成立,符合题意;解得-2不等式的性质是不等式这一章内容的理论基础,是不等式的证明和解不等式的主要依据.因此,要熟练掌握和运用不等式的性质.
2.一元二次不等式的求解方法
对于一元二次不等式ax2+bx+c>0(或≥0,<0,≤0)(其中a≠0)的求解,要联想两个方面的问题:二次函数y=ax2+bx+c与x轴的交点;方程ax2+bx+c=0的根.按照Δ>0,Δ=0,Δ<0分三种情况讨论对应的一元二次不等式ax2+bx+c>0(或≥0,<0,≤0)(a≠0)的解集.3.二元一次不等式表示的平面区域的判定
对于在直线Ax+By+C=0同一侧的所有点(x,y),实数Ax+By+C的符号相同,取一个特殊点(x0,y0),根据实数Ax0+By0+C的正负即可判断不等式表示直线哪一侧的平面区域,可简记为“直线定界,特殊点定域”.特别地,当C≠0时,常取原点作为特殊点.
4.求目标函数最优解的方法
通过平移目标函数所对应的直线,可以发现取得最优解对应的点往往是可行域的顶点(或边界),于是在选择题中关于线性规划的最值问题,可采用求解方程组代入检验的方法求解.5.运用均值不等式求最值时把握三个条件
①“一正”——各项为正数;
②“二定”——“和”或“积”为定值;
③“三相等”——等号一定能取到.
这三个条件缺一不可.
2.能熟练利用不等式的性质比较大小、变形不等式、证明不等式.
3.会用均值不等式证明不等式,求解最值问题.
4.体会“三个二次”之间的内在联系在解决问题中的作用.
5.能熟练地运用图解法解决线性规划问题.NEIRONGSUOYIN内容索引知识梳理题型探究达标检测1知识梳理PART ONE知识梳理1.不等式的性质ZHISHISHULI<>>>><>>>>2.均值不等式
利用均值不等式证明不等式和求最值的区别
(1)利用均值不等式证明不等式,只需关注不等式成立的条件.
(2)利用均值不等式求最值,需要同时关注三个限制条件:一正;二定;三相等.3.三个二次之间的关系4.线性规划问题求解步骤
(1)把问题要求转化为约束条件;
(2)根据约束条件作出可行域;
(3)对目标函数变形并解释其几何意义;
(4)移动目标函数寻找最优解;
(5)解相关方程组求出最优解.2题型探究PART TWO题型一 利用均值不等式求最值4解析 y=a1-x(a>0,a≠1)的图象恒过定点 A(1,1),
∵点A在直线mx+ny-1=0上,∴m+n=1,反思感悟 当所给附加条件是一个等式时,常见的用法有两个:一个是用这个等式消元,化为命题角度1的类型;一个是直接利用该等式代入,或构造定值.题型二 “三个二次”之间的关系-14∴a+b=-14.反思感悟 (1)“三个二次”之间要选择一个运算简单的方向进行转化.
(2)用不等式组来刻画两根的位置体现了数形结合的思想.跟踪训练2 设不等式x2-2ax+a+2≤0的解集为M,如果M?[1,4],求实数a的取值范围.解 M?[1,4]有两种情况:
其一是M=?,此时Δ<0;其二是M≠?,此时Δ=0或Δ>0,下面分三种情况计算a的取值范围.
设f(x)=x2-2ax+a+2,
对方程x2-2ax+a+2=0,
有Δ=(-2a)2-4(a+2)=4(a2-a-2),
①当Δ<0时,-1
当a=-1时,M={-1} ? [1,4],不满足题意;
当a=2时,M={2}?[1,4],满足题意.③当Δ>0时,a<-1或a>2.
设方程f(x)=0的两根为x1,x2,且x1
当a<0时,a
当a=0时,a2=a,原不等式的解集为{x|x≠0,x∈R};
当0
当a=1时,a2=a,原不等式的解集为{x|x≠1,x∈R};
当a>1时,a
综上所述,当a<0或a>1时,原不等式的解集为{x|x
当0
当a=1时,原不等式的解集为{x|x≠1,x∈R};
当a=0时,原不等式的解集为{x|x≠0,x∈R}.反思感悟 对于含参数的一元二次不等式,若二次项系数为常数,则可先考虑分解因式,再对参数进行讨论;若不易分解因式,则可对判别式分类讨论,分类要不重不漏.跟踪训练3 已知常数a∈R,解关于x的不等式ax2-2x+a<0.解 (1)若a=0,则原不等式为-2x<0,故解集为{x|x>0}.
(2)若a>0,Δ=4-4a2.
①当Δ>0,即0
∴当a=-1时,原不等式的解集为{x|x∈R且x≠-1}.
③当Δ<0,即a<-1时,原不等式的解集为R.
综上所述,当a≥1时,原不等式的解集为?;当a=0时,原不等式的解集为{x|x>0};当a=-1时,原不等式的解集为{x|x∈R且x≠-1};
当a<-1时,原不等式的解集为R.题型四 线性规划问题解 如图,阴影部分(含边界)为不等式组所表示的可行域.设l0:2x+y=0,l:2x+y=z,则z的几何意义是直线y=-2x+z在y轴上的截距,显然,直线越往上移动,对应在y轴上的截距越大,即z越大;直线越往下移动,对应在y轴上的截距越小,即z越小.
上下平移直线l0,可得当l0过点A(5,2)时,zmax=2×5+2=12;
当l0过点B(1,1)时,zmin=2×1+1=3.反思感悟 (1)因为最优解与可行域的边界斜率有关,所以画可行域要尽可能精确.
(2)线性目标函数的最值与纵截距不一定是增函数关系,所以要关注纵截距越大,z越大还是越小.跟踪训练4 某人承揽一项业务,需做文字标牌4个,绘画标牌5个.现有两种规格的原料,甲种规格每张3 m2,可做文字标牌1个,绘画标牌2个;乙种规格每张2 m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张才能使得总用料面积最小.解 设需要甲种原料x张,乙种原料y张,
则可做文字标牌(x+2y)个,绘画标牌(2x+y)个,所用原料的总面积为z=3x+2y,
作出可行域如图阴影部分(含边界)所示.在一组平行直线3x+2y=z中,
经过可行域内的点A时,z取得最小值,
直线2x+y=5和直线x+2y=4的交点为A(2,1),
即最优解为(2,1).
所以使用甲种规格原料2张,乙种规格原料1张,可使总的用料面积最小.3达标检测PART THREE12341.(2018·全国Ⅰ)已知集合A={x|x2-x-2>0},则?RA等于
A.{x|-1
C.{x|x<-1}∪{x|x>2}
D.{x|x≤-1}∪{x|x≥2}√解析 方法一 A={x|(x-2)(x+1)>0}={x|x<-1或x>2},
所以?RA={x|-1≤x≤2},故选B.
方法二 因为A={x|x2-x-2>0},
所以?RA={x|x2-x-2≤0}={x|-1≤x≤2},故选B.5取得最大值时的最优解有无穷多个,则实数m的值为1234√解析 作出不等式组表示的平面区域如图阴影部分(包含边界)所示,由图可知当直线y=mx-z(m≠0)与直线2x-2y+1=0重合,即m=1时,目标函数z=mx-y取最大值的最优解有无穷多个,故选A.51234A.-18 B.8 C.-13 D.1√512344.若不等式4(a-2)x2+2(a-2)x-1<0对一切x∈R恒成立,则a的取值范围
是_______.(-2,2]解析 不等式4(a-2)x2+2(a-2)x-1<0,当a-2=0,即a=2时,不等式恒成立,符合题意;解得-2
2.一元二次不等式的求解方法
对于一元二次不等式ax2+bx+c>0(或≥0,<0,≤0)(其中a≠0)的求解,要联想两个方面的问题:二次函数y=ax2+bx+c与x轴的交点;方程ax2+bx+c=0的根.按照Δ>0,Δ=0,Δ<0分三种情况讨论对应的一元二次不等式ax2+bx+c>0(或≥0,<0,≤0)(a≠0)的解集.3.二元一次不等式表示的平面区域的判定
对于在直线Ax+By+C=0同一侧的所有点(x,y),实数Ax+By+C的符号相同,取一个特殊点(x0,y0),根据实数Ax0+By0+C的正负即可判断不等式表示直线哪一侧的平面区域,可简记为“直线定界,特殊点定域”.特别地,当C≠0时,常取原点作为特殊点.
4.求目标函数最优解的方法
通过平移目标函数所对应的直线,可以发现取得最优解对应的点往往是可行域的顶点(或边界),于是在选择题中关于线性规划的最值问题,可采用求解方程组代入检验的方法求解.5.运用均值不等式求最值时把握三个条件
①“一正”——各项为正数;
②“二定”——“和”或“积”为定值;
③“三相等”——等号一定能取到.
这三个条件缺一不可.
