10.3.2 旋转的特征 课件
图片预览




文档简介
课件17张PPT。10.3 旋转2、 旋转的特征在平面内,将一个图形绕着一个定点沿着某个方向转动一个角度,这样的图形运动,称为旋转。这个定点称为旋转中心,转动的角称为旋转角。旋转的定义 观察右图,请分析其中的变化过程。45°A? B? 探索一1、△AOB与 △ A? OB? 能够完全重合
2、 OA=OA? , OB=OB? , AB=A? B? ;
∠AOB=∠A? OB? , ∠A=∠A? , ∠B=∠B? .
3、 OA=OA? , OB=OB? ;
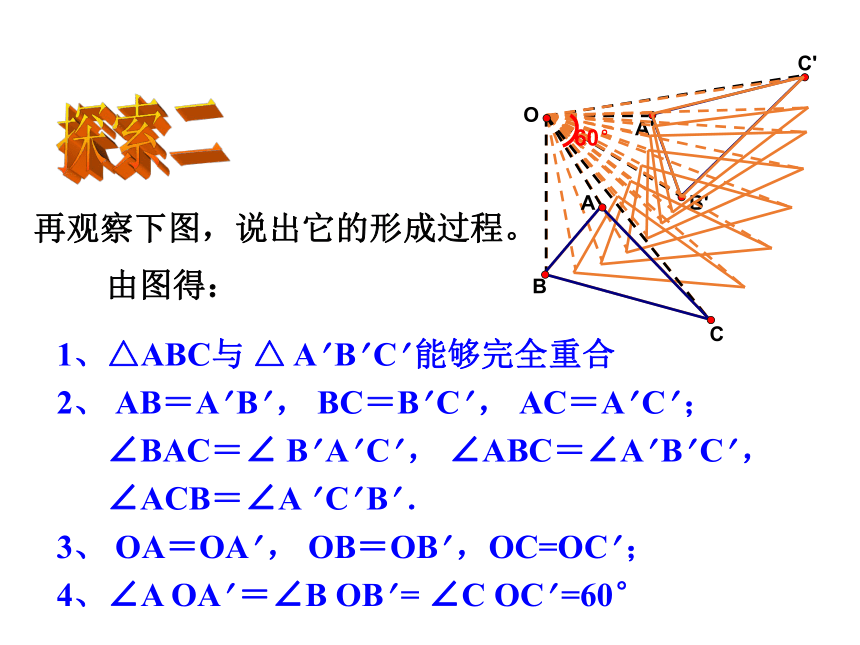
4、∠A OA? =∠B OB? =45° 由图得: 再观察下图,说出它的形成过程。O60°探索二1、△ABC与 △ A? B? C? 能够完全重合
2、 AB=A? B? , BC=B? C? , AC=A? C? ;
∠BAC=∠ B? A? C? , ∠ABC=∠A? B? C? ,
∠ACB=∠A ? C? B? .
3、 OA=OA? , OB=OB? ,OC=OC? ;
4、∠A OA? =∠B OB? = ∠C OC? =60° 由图得:1、旋转不改变图形的形状和大小;
2、旋转前后对应线段相等,对应角相等;
3、对应点到旋转中心的距离相等;
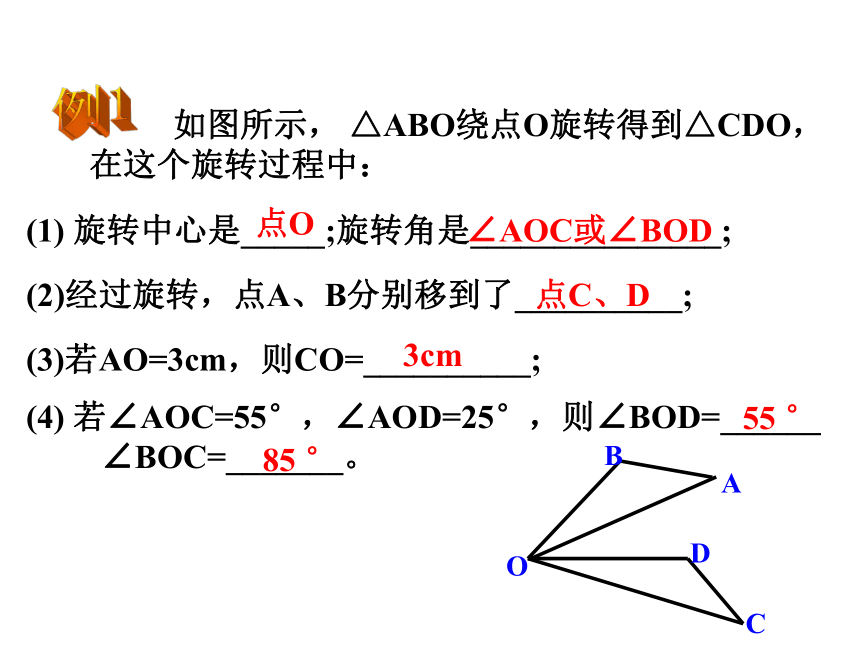
4、任意一对对应点与旋转中心的连线所成的角都是旋转角.旋转的特征 如图所示, △ABO绕点O旋转得到△CDO,在这个旋转过程中:(1) 旋转中心是_____;旋转角是_______________;(2)经过旋转,点A、B分别移到了__________;(3)若AO=3cm,则CO=__________;(4) 若∠AOC=55°,∠AOD=25°,则∠BOD=______
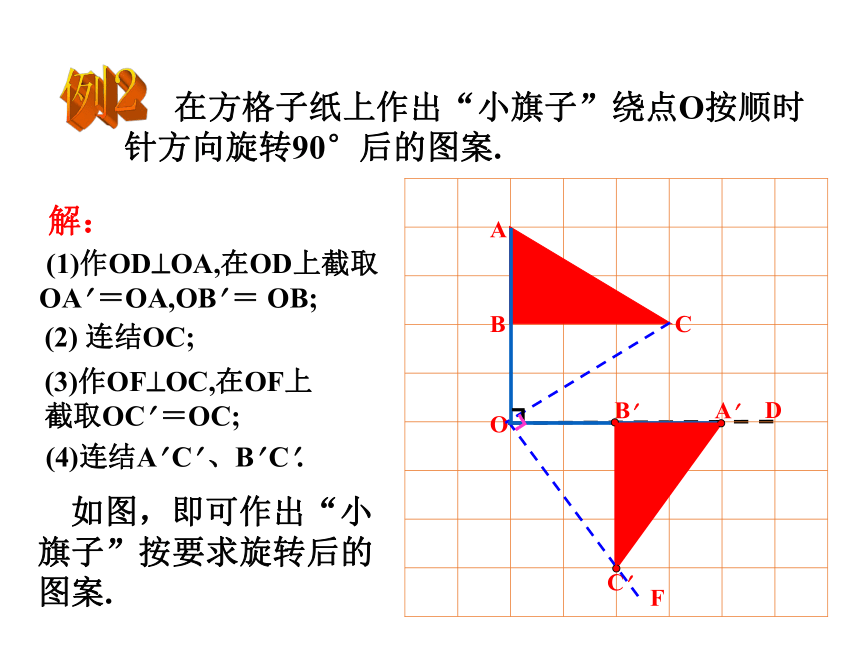
∠BOC=_______。点O ∠AOC或∠BOD点C、D3cm55 °85 °例1A? B? C? 在方格子纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案. (1)作OD?OA,在OD上截取OA? =OA,OB? = OB;(2) 连结OC;(3)作OF?OC,在OF上截取OC? =OC; (4)连结A? C? 、B? C?.┓┓ 如图,即可作出“小旗子”按要求旋转后的图案.解:例2DF旋转作图的步骤1、确定旋转中心和旋转角的大小,旋转的方向;
2、确定关键点旋转后的对应点;
3、顺次连结各对应点,得到旋转后的图形。 如图,在正方形ABCD中, △ABE旋转后能与△ADF重合O(1)旋转中心是哪一点? 请在图中画出并说明理由;(2)旋转了多少度? (3)说出线段AF与BE的关系?旋转中心在对应点连线的垂直平分线上,如图点O即为所求如图∠AOD即为旋转角,顺时针旋转90 °例3 如图,在正方形ABCD中, △ABE旋转后能与△ADF重合(3)说出线段AF与BE的关系?解:相等且互相垂直,证明如下:
∵ △ ABE旋转后能与△ ADF重合
∴AF=BE且∠1=∠2,
又∠2+∠3=90°
∴∠1+∠3=90°
∴∠AOE=90°即AF⊥BE
∴AF=BE 且AF⊥BE例3 1、如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋转后到达△CAE的位置。问:AECBD(1)旋转中心是_____,旋转的度数是____ (2)若已知∠DCB=20°,则∠CDB=_______, ∠AEC=____, ∠BAE=____(3)如果连结DE,那么
△DCE是_________三角形。点C90°115°90°等腰直角115°2、 如图1,ΔABC和ΔADE都是等腰直角三角形,∠ACB和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2;两次旋转的角度分别为( ).A、45°,90° B、90°,45°
C、60°,30° D、30°,60°A3、画出△ABC绕点C逆时针旋转90°后的图形
(书本上122页练习3)A’B’1、掌握旋转的特征并灵活运用其特征;
2、能按要求作出简单平面图形旋转后的图形,能说出旋转中心与旋转角度;
3、能通过旋转前后图形找到旋转中心
(对应点所连线段的中垂线的交点)如图是一个直角三角形的苗圃,有正方形花坛和两块直角三角形的草皮组成,如果两个直角三角形的两条斜边长分别为3米和6米,问草皮的面积是多少?思考题如图 :通过旋转图形,我们可以把两个直角三角形拼结成一个直角三角形,而这个直角三角形的两条直角边正好是3米和6米。再 见
2、 OA=OA? , OB=OB? , AB=A? B? ;
∠AOB=∠A? OB? , ∠A=∠A? , ∠B=∠B? .
3、 OA=OA? , OB=OB? ;
4、∠A OA? =∠B OB? =45° 由图得: 再观察下图,说出它的形成过程。O60°探索二1、△ABC与 △ A? B? C? 能够完全重合
2、 AB=A? B? , BC=B? C? , AC=A? C? ;
∠BAC=∠ B? A? C? , ∠ABC=∠A? B? C? ,
∠ACB=∠A ? C? B? .
3、 OA=OA? , OB=OB? ,OC=OC? ;
4、∠A OA? =∠B OB? = ∠C OC? =60° 由图得:1、旋转不改变图形的形状和大小;
2、旋转前后对应线段相等,对应角相等;
3、对应点到旋转中心的距离相等;
4、任意一对对应点与旋转中心的连线所成的角都是旋转角.旋转的特征 如图所示, △ABO绕点O旋转得到△CDO,在这个旋转过程中:(1) 旋转中心是_____;旋转角是_______________;(2)经过旋转,点A、B分别移到了__________;(3)若AO=3cm,则CO=__________;(4) 若∠AOC=55°,∠AOD=25°,则∠BOD=______
∠BOC=_______。点O ∠AOC或∠BOD点C、D3cm55 °85 °例1A? B? C? 在方格子纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案. (1)作OD?OA,在OD上截取OA? =OA,OB? = OB;(2) 连结OC;(3)作OF?OC,在OF上截取OC? =OC; (4)连结A? C? 、B? C?.┓┓ 如图,即可作出“小旗子”按要求旋转后的图案.解:例2DF旋转作图的步骤1、确定旋转中心和旋转角的大小,旋转的方向;
2、确定关键点旋转后的对应点;
3、顺次连结各对应点,得到旋转后的图形。 如图,在正方形ABCD中, △ABE旋转后能与△ADF重合O(1)旋转中心是哪一点? 请在图中画出并说明理由;(2)旋转了多少度? (3)说出线段AF与BE的关系?旋转中心在对应点连线的垂直平分线上,如图点O即为所求如图∠AOD即为旋转角,顺时针旋转90 °例3 如图,在正方形ABCD中, △ABE旋转后能与△ADF重合(3)说出线段AF与BE的关系?解:相等且互相垂直,证明如下:
∵ △ ABE旋转后能与△ ADF重合
∴AF=BE且∠1=∠2,
又∠2+∠3=90°
∴∠1+∠3=90°
∴∠AOE=90°即AF⊥BE
∴AF=BE 且AF⊥BE例3 1、如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋转后到达△CAE的位置。问:AECBD(1)旋转中心是_____,旋转的度数是____ (2)若已知∠DCB=20°,则∠CDB=_______, ∠AEC=____, ∠BAE=____(3)如果连结DE,那么
△DCE是_________三角形。点C90°115°90°等腰直角115°2、 如图1,ΔABC和ΔADE都是等腰直角三角形,∠ACB和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2;两次旋转的角度分别为( ).A、45°,90° B、90°,45°
C、60°,30° D、30°,60°A3、画出△ABC绕点C逆时针旋转90°后的图形
(书本上122页练习3)A’B’1、掌握旋转的特征并灵活运用其特征;
2、能按要求作出简单平面图形旋转后的图形,能说出旋转中心与旋转角度;
3、能通过旋转前后图形找到旋转中心
(对应点所连线段的中垂线的交点)如图是一个直角三角形的苗圃,有正方形花坛和两块直角三角形的草皮组成,如果两个直角三角形的两条斜边长分别为3米和6米,问草皮的面积是多少?思考题如图 :通过旋转图形,我们可以把两个直角三角形拼结成一个直角三角形,而这个直角三角形的两条直角边正好是3米和6米。再 见
