10.4 中心对称 课件(34张PPT)
文档属性
| 名称 | 10.4 中心对称 课件(34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 737.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 10:33:00 | ||
图片预览







文档简介
课件34张PPT。第10章 轴对称、平移与旋转10.4 中心对称1课堂讲解中心对称图形
两个图形成中心对称
中心对称的性质2课时流程逐点
导讲练课堂小结作业提升 如图,魔术师把 4 张扑克牌放在桌子上,然后转
过身去,请一位观众把某两张牌旋转 180°,魔术师
转过身来,看到 4 张扑克牌仍如原样放置.但是,他
很快确定了哪两张牌被旋转过.你能说明其中的奥妙
吗?1知识点中心对称图形 在上一节,我们已经看到有不少图形绕某一中心
旋转一定角度后,可以与自身重合. 如图所示的三个
图形都是这样的旋转对称图形. 上图中间的一个图形绕着中心旋转180°后能与
自身重合,我们把这种图形叫做中心对称图形 (a
figure of central symmetry ),这个中心叫做对称中心
(centre of symmetry).1. 定义:把一个图形绕着某一个点旋转180°,如果
能与自身重合,我们把这种图形叫做中心对称图形,
这个中心叫做对称中心.
要点精析:
(1)中心对称图形的对称中心一定在图形内;
(2)中心对称图形是针对一个图形而言的;
(3)中心对称图形上所有的点关于对称中心的对称点
都在这个图形本身上;(4)中心对称图形一定是旋转对称图形,但旋转对称
图形不一定是中心对称图形;
(5)常见的中心对称图形有:线段、圆、平行四边形、
长方形、正方形、边数是偶数的正多边形,它们
的对称中心分别是线段的中点、圆的圆心、各种
特殊四边形的对角线的交点,边数是偶数的正多
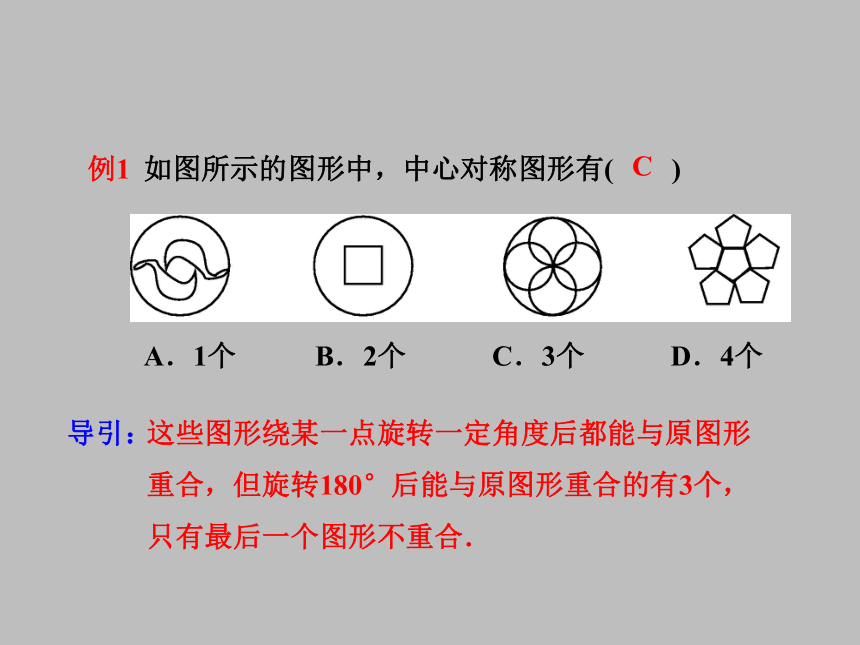
边形的对角线的交点.如图所示的图形中,中心对称图形有( )
A.1个 B.2个 C.3个 D.4个
例1导引:这些图形绕某一点旋转一定角度后都能与原图形
重合,但旋转180°后能与原图形重合的有3个,
只有最后一个图形不重合.C 正多边形图案为中心对称图形的识别方法:边数
为偶数的正多边形图案是中心对称图形,相应地,与
边数为偶数的正多边形具有类似特征的图形是中心对
称图形;边数为奇数的正多边形或具有类似特征的图
形一定不是中心对称图形.1(贺州)下列图形中既是轴对称图形,又是中心对称图形的是( )
A.等边三角形
B.平行四边形
C.正方形
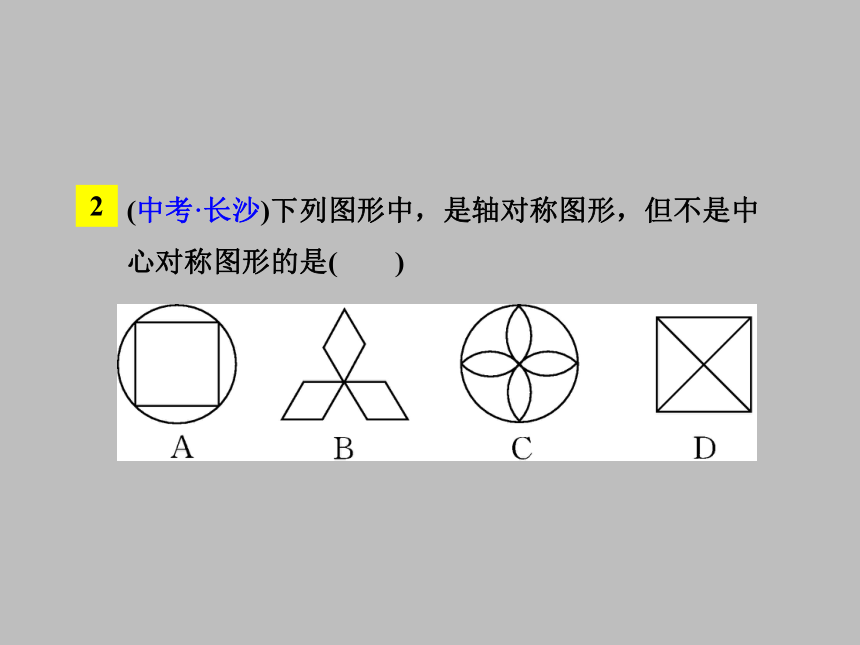
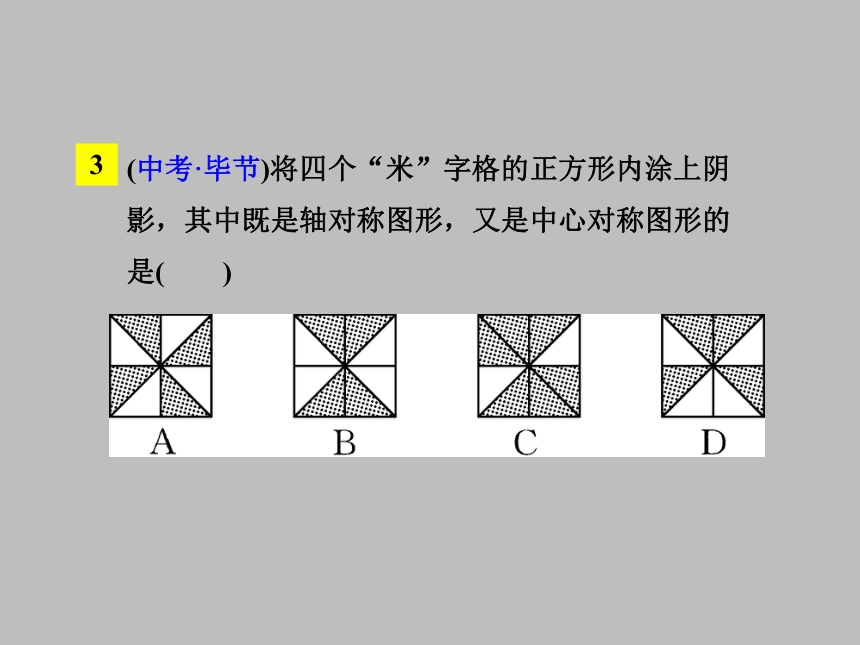
D.正五边形2(中考·长沙)下列图形中,是轴对称图形,但不是中心对称图形的是( )3(中考·毕节)将四个“米”字格的正方形内涂上阴影,其中既是轴对称图形,又是中心对称图形的是( )2知识点两个图形成中心对称 把一个图形绕着某一点旋转180°,如果它能够和
另一个图形重合,那么,我们就说这两个图形成中心
对称,这个点叫做对称中心,这两个图形中的对应点,
叫做关于中心的对称点. 如图所示,△ABC与△ADE是
成中心对称的两个三角形,点A是
对称中心,点B的对称点为点____,
点C的对称点为点____,点A的对称
点为点____.
点B绕着点A旋转180°到达点D处,因此,B、A、
D点在同一条直线上,并且AB=AD. 在平面内,把一个图形绕着某一点旋转180°,如果
它能够与另一个图形重合,那么就说这两个图形关
于这个点对称或(成)中心对称,这个点叫做对称中
心. 这两个图形在旋转后能重合的对应点叫做关于对
称中心的对称点.要点精析:
(1)中心对称是特殊的旋转,其旋转角为180°;
(2)中心对称是指两个图形的位置关系,必须涉及两个
图形,其中一个图形绕对称中心旋转180°后一定
能与另一个图形重合;
(3)成中心对称的两个图形,只有一个对称中心,这个
对称中心可能在每个图形的外部,也可能在每个图
形的内部或边上,但对称点一定在对称中心的两侧
或与对称中心重合.如图所示的图形中,成中心对称的有______组.例2导引:利用中心对称的定义解答.3 根据中心对称的定义,看左边的图形能否绕一点
旋转180°后与右边的图形重合,能重合则是中心对
称,否则就不是,本例中第四组不是.1如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,图中哪些三角形关于点O成中心对称?2下列说法中正确的是( )
A.形状和大小完全相同的两个图形成中心对称
B.成中心对称的两个图形必须重合
C.成中心对称的两个图形形状和大小完全相同
D.旋转后能够重合的两个图形成中心对称3下列4组图形中,右边的图形与左边的图形成中心对称的是( )3知识点中心对称的性质 在图中, △A′B′C′与△ABC关于点O成中心对称,
你能从图中找到哪些等量关系?
我们可以发现,点A绕中心
点O旋转180°后到点A′,于是
A、O、A′三点在同一条直线上,
并且OA =OA′.另外分别在同一
条直线上的三点还有_____和_____;并且OB=_____,
OC =_____. 在成中心对称的两个图形中,连结对称点的线段
都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的所有对应点连成的线段
都经过某一点,并且都被该点平分,那么这两个图形
关于这一点成中心对称.1. 中心对称的性质:
(1)具有旋转的一切性质(因为中心对称是一种特殊的
旋转);
(2)在成中心对称的两个图形中,连结对称点的线段
都经过对称中心,而且被对称中心所平分;
(3)如果两个图形的所有对应点连成的线段都经过某
一点,并且都被该点平分,那么这两个图形关于
这点中心对称.2.确定成中心对称的两个图形的对称中心的方法:
(1)连结任意一对对称点,取这条线段的中点,这个
中点就是对称中心.
(2)连结任意两对对称点,两条线段的交点就是对称
中心.如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.例3解:(1)连结AO并延长AO到点D,使OD=OA,于是得
到点A关于点O的对称点D;
(2)同样画出点B和点C关于点O的对称点E和F;
(3)顺次连结DE、EF、FD.
如图,△DFF即为所求
的三角形. 本题运用了转化思想.利用中心对称的特征先找
出图形上的关键点,再作出关键点的对称点,从而将
图形的问题转化为点的问题,把复杂问题转化为简单
问题来解决.1如图,点O是四边形ABCD的边AB的中点,画出以点O为对称中心,与四边形ABCD成中心对称的图形.2如图,△ABC绕点O旋转180°得到△DEF,下列说法错误的是( )
A.△ABC与△DEF关于点B成中心对称
B.点B和点E关于点O对称
C.AB∥DE
D.CE=BF3△ABC和△A′B′C′关于点O对称(点O不在直线AB
上),下列结论中不正确的是( )
A.OA=A′O
B.AB∥A′B′
C.CO=BC
D.∠BAC=∠B′A′C′(1)连接两对对应点,则线段的交点即为对称中心;
(2)中心对称作图的方法步骤:
① 确定对称中心 ②作关键点的对称点
③连线 ④写结论;
(3)每一对对应点所连线段被对称中心平分是识别
中心对称图形的重要依据.
两个图形成中心对称
中心对称的性质2课时流程逐点
导讲练课堂小结作业提升 如图,魔术师把 4 张扑克牌放在桌子上,然后转
过身去,请一位观众把某两张牌旋转 180°,魔术师
转过身来,看到 4 张扑克牌仍如原样放置.但是,他
很快确定了哪两张牌被旋转过.你能说明其中的奥妙
吗?1知识点中心对称图形 在上一节,我们已经看到有不少图形绕某一中心
旋转一定角度后,可以与自身重合. 如图所示的三个
图形都是这样的旋转对称图形. 上图中间的一个图形绕着中心旋转180°后能与
自身重合,我们把这种图形叫做中心对称图形 (a
figure of central symmetry ),这个中心叫做对称中心
(centre of symmetry).1. 定义:把一个图形绕着某一个点旋转180°,如果
能与自身重合,我们把这种图形叫做中心对称图形,
这个中心叫做对称中心.
要点精析:
(1)中心对称图形的对称中心一定在图形内;
(2)中心对称图形是针对一个图形而言的;
(3)中心对称图形上所有的点关于对称中心的对称点
都在这个图形本身上;(4)中心对称图形一定是旋转对称图形,但旋转对称
图形不一定是中心对称图形;
(5)常见的中心对称图形有:线段、圆、平行四边形、
长方形、正方形、边数是偶数的正多边形,它们
的对称中心分别是线段的中点、圆的圆心、各种
特殊四边形的对角线的交点,边数是偶数的正多
边形的对角线的交点.如图所示的图形中,中心对称图形有( )
A.1个 B.2个 C.3个 D.4个
例1导引:这些图形绕某一点旋转一定角度后都能与原图形
重合,但旋转180°后能与原图形重合的有3个,
只有最后一个图形不重合.C 正多边形图案为中心对称图形的识别方法:边数
为偶数的正多边形图案是中心对称图形,相应地,与
边数为偶数的正多边形具有类似特征的图形是中心对
称图形;边数为奇数的正多边形或具有类似特征的图
形一定不是中心对称图形.1(贺州)下列图形中既是轴对称图形,又是中心对称图形的是( )
A.等边三角形
B.平行四边形
C.正方形
D.正五边形2(中考·长沙)下列图形中,是轴对称图形,但不是中心对称图形的是( )3(中考·毕节)将四个“米”字格的正方形内涂上阴影,其中既是轴对称图形,又是中心对称图形的是( )2知识点两个图形成中心对称 把一个图形绕着某一点旋转180°,如果它能够和
另一个图形重合,那么,我们就说这两个图形成中心
对称,这个点叫做对称中心,这两个图形中的对应点,
叫做关于中心的对称点. 如图所示,△ABC与△ADE是
成中心对称的两个三角形,点A是
对称中心,点B的对称点为点____,
点C的对称点为点____,点A的对称
点为点____.
点B绕着点A旋转180°到达点D处,因此,B、A、
D点在同一条直线上,并且AB=AD. 在平面内,把一个图形绕着某一点旋转180°,如果
它能够与另一个图形重合,那么就说这两个图形关
于这个点对称或(成)中心对称,这个点叫做对称中
心. 这两个图形在旋转后能重合的对应点叫做关于对
称中心的对称点.要点精析:
(1)中心对称是特殊的旋转,其旋转角为180°;
(2)中心对称是指两个图形的位置关系,必须涉及两个
图形,其中一个图形绕对称中心旋转180°后一定
能与另一个图形重合;
(3)成中心对称的两个图形,只有一个对称中心,这个
对称中心可能在每个图形的外部,也可能在每个图
形的内部或边上,但对称点一定在对称中心的两侧
或与对称中心重合.如图所示的图形中,成中心对称的有______组.例2导引:利用中心对称的定义解答.3 根据中心对称的定义,看左边的图形能否绕一点
旋转180°后与右边的图形重合,能重合则是中心对
称,否则就不是,本例中第四组不是.1如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,图中哪些三角形关于点O成中心对称?2下列说法中正确的是( )
A.形状和大小完全相同的两个图形成中心对称
B.成中心对称的两个图形必须重合
C.成中心对称的两个图形形状和大小完全相同
D.旋转后能够重合的两个图形成中心对称3下列4组图形中,右边的图形与左边的图形成中心对称的是( )3知识点中心对称的性质 在图中, △A′B′C′与△ABC关于点O成中心对称,
你能从图中找到哪些等量关系?
我们可以发现,点A绕中心
点O旋转180°后到点A′,于是
A、O、A′三点在同一条直线上,
并且OA =OA′.另外分别在同一
条直线上的三点还有_____和_____;并且OB=_____,
OC =_____. 在成中心对称的两个图形中,连结对称点的线段
都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的所有对应点连成的线段
都经过某一点,并且都被该点平分,那么这两个图形
关于这一点成中心对称.1. 中心对称的性质:
(1)具有旋转的一切性质(因为中心对称是一种特殊的
旋转);
(2)在成中心对称的两个图形中,连结对称点的线段
都经过对称中心,而且被对称中心所平分;
(3)如果两个图形的所有对应点连成的线段都经过某
一点,并且都被该点平分,那么这两个图形关于
这点中心对称.2.确定成中心对称的两个图形的对称中心的方法:
(1)连结任意一对对称点,取这条线段的中点,这个
中点就是对称中心.
(2)连结任意两对对称点,两条线段的交点就是对称
中心.如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.例3解:(1)连结AO并延长AO到点D,使OD=OA,于是得
到点A关于点O的对称点D;
(2)同样画出点B和点C关于点O的对称点E和F;
(3)顺次连结DE、EF、FD.
如图,△DFF即为所求
的三角形. 本题运用了转化思想.利用中心对称的特征先找
出图形上的关键点,再作出关键点的对称点,从而将
图形的问题转化为点的问题,把复杂问题转化为简单
问题来解决.1如图,点O是四边形ABCD的边AB的中点,画出以点O为对称中心,与四边形ABCD成中心对称的图形.2如图,△ABC绕点O旋转180°得到△DEF,下列说法错误的是( )
A.△ABC与△DEF关于点B成中心对称
B.点B和点E关于点O对称
C.AB∥DE
D.CE=BF3△ABC和△A′B′C′关于点O对称(点O不在直线AB
上),下列结论中不正确的是( )
A.OA=A′O
B.AB∥A′B′
C.CO=BC
D.∠BAC=∠B′A′C′(1)连接两对对应点,则线段的交点即为对称中心;
(2)中心对称作图的方法步骤:
① 确定对称中心 ②作关键点的对称点
③连线 ④写结论;
(3)每一对对应点所连线段被对称中心平分是识别
中心对称图形的重要依据.
