10.5 图形的全等 课件(38张PPT)
文档属性
| 名称 | 10.5 图形的全等 课件(38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 684.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 00:00:00 | ||
图片预览







文档简介
课件38张PPT。第10章 轴对称、平移与旋转10.5 图形的全等1课堂讲解全等图形
全等三角形及其对应元素
全等三角形的性质2课时流程逐点
导讲练课堂小结作业提升 课间操时间,小明和小聪在操场上突然争论起来,
他们都说比对方长得高,这时数学老师走过来,笑着
对他们说:“你们不用争了,比一下你们俩地上的影
子,如果一样长就说明你们一样高.”你知道数学老师
为什么能从他们的影长相等就判
定他们的身高相同吗? 学习了全
等图形的有关知识,我们就可以
说明其中的道理了.1知识点全等图形 我们已经认识了图形的轴对称、平移和旋转,这
是图形的三种基本变换,图形经过这样的变换,位置
发生了改变,但变换前后两个图形的对应线段相等,
对应角相等,图形的形状和大小并没有改变. 要想知道两个图形的形状和大小是否完全相同,
可以通过轴对称、平移和旋转这些图形的变换,把两
个图形叠合在一起,观察它们是否完全重合. 能够完
全重合的两个图形叫做全等图形(congruent figures).1. 定义:能够完全重合的两个图形叫做全等图形.
要点精析:
(1)图形的全等与它们的位置无关,只要满足能够完
全重合即可;而完全重合包含两层含义:图形的
形状相同,大小相等;
(2)全等形的周长、面积分别相等,但周长或面积相
等的两个图形不一定全等.
2. 几种常用全等变换的方式:轴对称、平移、旋转.下图中是全等图形的是_____________________
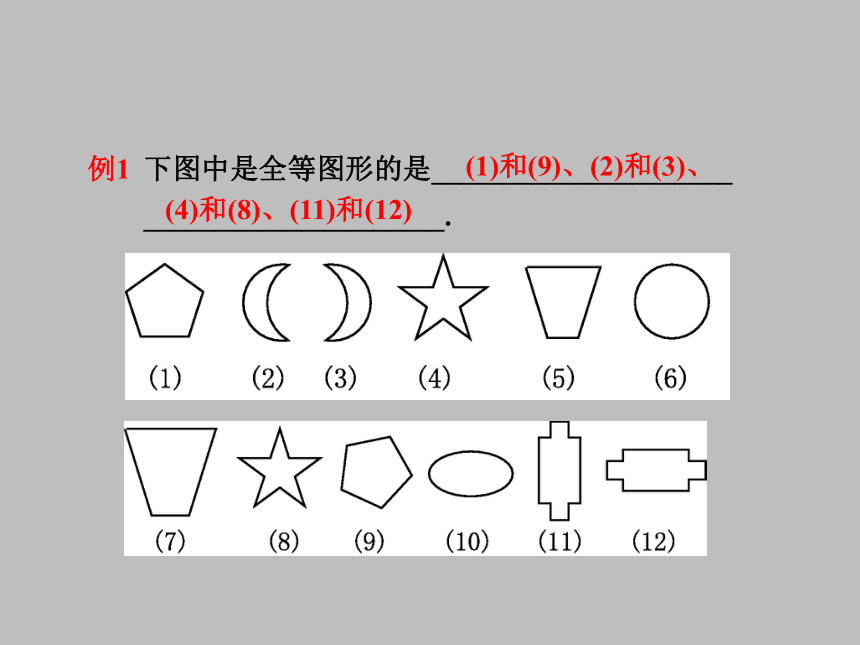
_____________________.例1(1)和(9)、(2)和(3)、(4)和(8)、(11)和(12)导引:上述图形中,(5)和(7)形状相同,但大小不同,(6)
和(10)形状不同,故都不是全等图形;(1)和(9)、
(2)和(3)、(11)和(12)尽管方向不同,但大小、形
状完全相同,所以它们是全等图形;(4)和(8)都是
五角星,大小、形状都相同,是全等图形.(1)此题运用定义识别全等图形,确定两个图形全等
要符合两个条件:①形状相同,②大小相等;是
不是全等图形与位置无关.
(2)判断两个图形是否全等还可以通过平移、旋转、
翻折等方法把两个图形叠合在一起,看它们能否
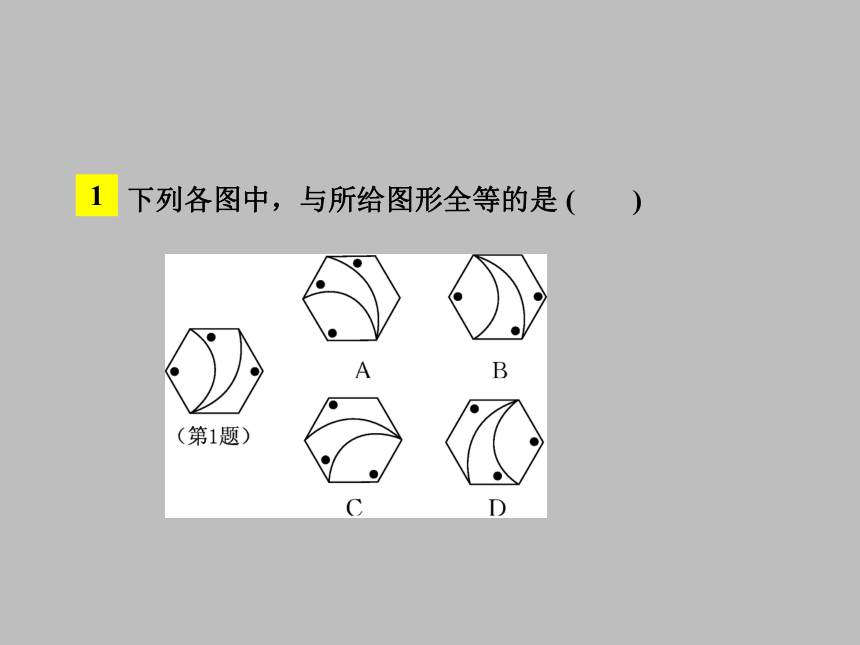
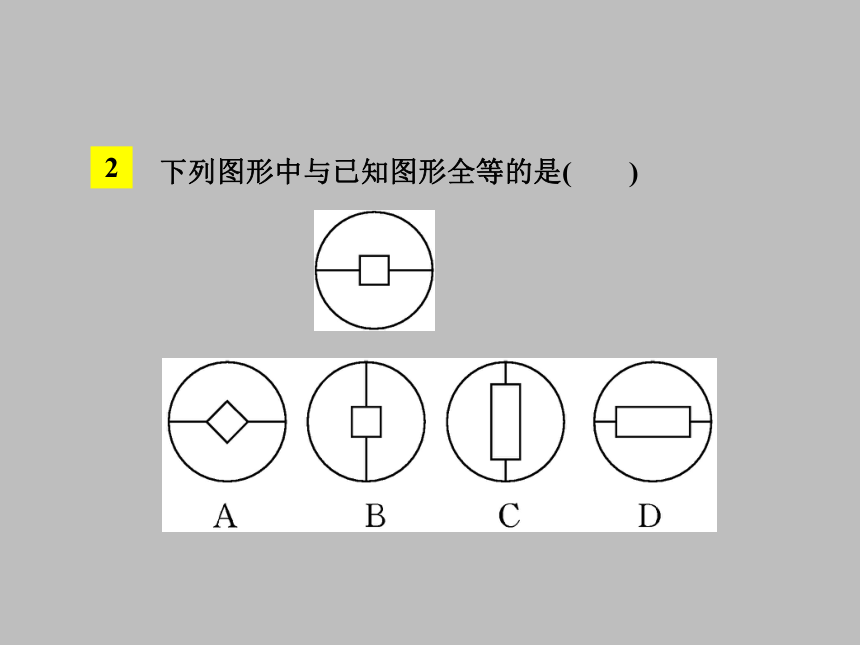
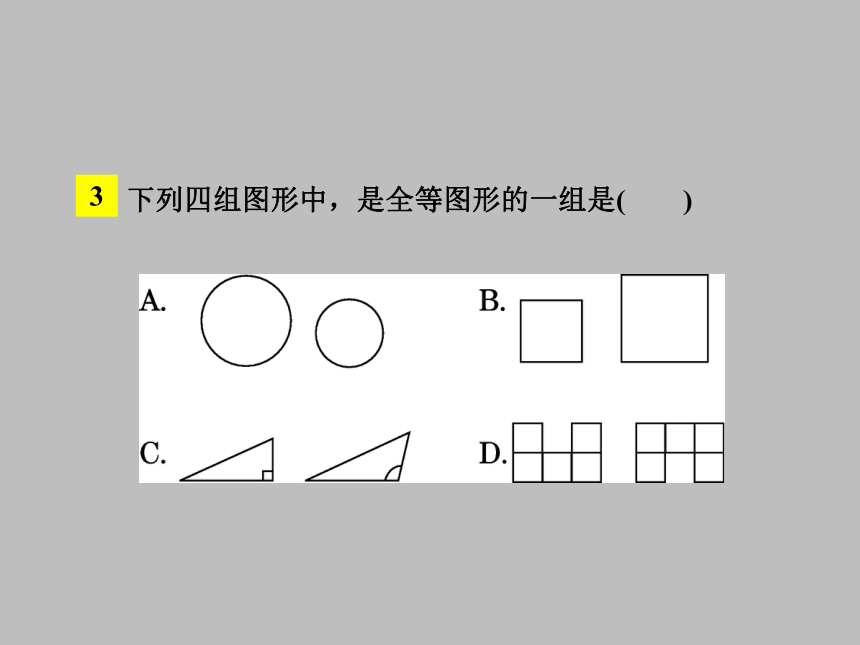
重合,即用叠合法判断.1下列各图中,与所给图形全等的是 ( )2下列图形中与已知图形全等的是( )3下列四组图形中,是全等图形的一组是( )2知识点全等三角形及其对应元素 如图中给出了 8个图形,你能发现哪两个图形是
全等图形吗?
动手试试看. 一个图形经过轴对称、平移和旋转等变换所得到
的新图形一定与原图形全等;反过来,两个全等的图
形经过上述变换后一定能够互相重合.
思考:观察图中的
两对多边形,每对
中的其中一个可以
经过怎样的变换和
另一个图形重合? 上面的两对多边形都是全等图形,也称为全等
多边形.两个全等的多边形,经过变换而重合,相互
重合的顶点叫做对应顶点,相互重合的边叫做对应
边,相互重合的角叫做对应角. 如图中的两个五边形是全等的,记作五边形
ABCDE≌五边形A′B′C′D′E′(这里,符号“≌”
表示全等, 读作“全等于”). 点A与点A′、点B与
点B′、点C与点C′、点D与点D′、点E与点E′分别是对应顶点. 依据上面的分析,我们知道:
全等多边形的对应边相等,对应角相等.
这就是全等多边形的性质.实际上,边、角分别
对应相等这两个特征足以刻画多边形的全等了.也就
是说,在数学上我们可以给出全等多边形如下的定
义:
边、角分别对应相等的两个多边形称为全等多
边形.1. 全等三角形的定义:如果两个三角形的边、角分
别对应相等,那么这两个三角形全等.
2. 全等三角形对应元素:把两个全等的三角形重合
到一起,(1)对应顶点:重合的顶点;(2)对应边:
重合的边;(3)对应角:重合的角.3. 全等三角形的表示法:如图,△ABC和△DEF全
等,记作△ABC≌△DEF,符号“≌”读作全等于.
其中“∽”表示形状相同,“=”表示大小相等.记
两个三角形全等时,通常把表示对应顶点的字母
写在对应的位置上,如点A和点D ,点B和点E ,
点C和点F 是对应顶点;AB和DE,BC和EF ,AC
和DF是对应边;∠A和∠D,∠B和∠E ,∠C和
∠F是对应角.4. 对应元素的确定方法:
(1)字母顺序确定法:根据书写规范,按照对应顶点
确定对应边、对应角,如△CAB≌△FDE,则
AB与DE、AC与DF、BC与EF是对应边,∠A和
∠D、∠B和∠E、∠C和∠F是对应角.
(2)图形位置确定法:①公共边一定是对应边;②公
共角一定是对应角;③对顶角一定是对应角.
(3)图形大小确定法:两个全等三角形的最大的边(角)
是对应边(角),最小的边(角)是对应边(角).5. 对应边(或角)与对边(或角)的区别:对应边、对应
角是对两个三角形而言的,指两条边、两个角的
关系;而对边、对角是指一个三角形的边和角的
位置关系. 对边是与角相对的边,对角是与边相对
的角.
6. 易错警示:记两个三角形全等时,通常把表示对
应顶点的字母写在对应的位置上,字母顺序不能
随意书写.如图,△ACB≌△BDA,AC和BD对应,BC和
AD对应,写出其他的对应边及对应角.例2因为已经知道了两组对应边,所以剩下的一组边是
对应边.根据对应边所对的角是对应角,容易发现
AC的对角∠CBA和BD的对角∠DAB是对应角,
BC的对角∠CAB和AD的对角∠DBA是对应角,剩
下的一组角∠ACB和∠BDA是对应角.导引:解:其他的对应边是AB和BA;对应角是∠CBA和
∠DAB,∠CAB和∠DBA,∠ACB和∠BDA. 根根据对应边(角)找对应角(边)的方法:对应边
所对的角是对应角,对应角所对的边是对应边.1如图,△ABC≌△EDC,∠ACB和∠ECD是对应角,BC与DC是对应边,写出其他的对应边及对应角.2如图,沿直线AC对折,△ABC与△ADC重合,则△ABC≌________,AB的对应边是________,∠BCA的对应角是________________.知2-练3如图,将△ABC沿BC所在的直线平移到△A′B′C′
的位置,则△ABC________△A′B′C′,图中∠A与______,∠B与________,∠ACB与_________是
对应角.3知识点全等三角形的性质知3-导 三角形是特殊的多边形,因此,
全等三角形的对应边、对应角分别相等.
同样,我们也可以得到全等三角形的定义,从
而也得到了判断两个三角形是否全等的准确方法:
如果两个三角形的边、角分别对应相等,那么
这两个 三角形全等. 如图所示,△ABC≌△DEF,且∠A=∠D,
∠B=∠E. 你能指出它们之间其他的对应顶点、对应
角和对应边吗?知3-导知3-讲1.性质:全等三角形的对应边相等 ,对应角相等.
要点精析:
(1)全等三角形的对应元素相等.其中,对应元素包
括:对应边、对应角、对应中线、对应高、对应
角平分线、周长、面积等.
(2)在应用全等三角形的性质时,要先确定两个条件:
①两个三角形全等;②找对应元素.
(3)全等三角形的性质是说明线段、角相等的常用
方法.知3-讲2.全等三角形的判定:如果两个三角形的边角分别对
应相等,那么这两个三角形全等.
3.易错警示:周长相等的两个三角形不一定全等,面
积相等的两个三角形也不一定全等.知3-讲如图,△ABC沿着BC的方向平移至△DEF,∠A=80°,∠B=60°,求∠F的度数.例3知3-讲解:由图形平移的特征,可知与△ABC与△DEF的形状
与大小相同,即
△ABC≌△DEF.
∴ ∠D=∠A=80°(全等三角形的对应角相等).
同理∠DEF=∠B=60°.
又∵∠D+∠DEF+∠F = 180°(三角形的内角和
等于180°),
∴∠F=180°-∠D-∠DEF
=180°-80°-60°=40°.(1)全等三角形的性质在几何计算中起着重要作用,
当所求线段不是全等三角形的对应边时,可利用
等式的性质进行转换,从而找到所求线段与已知
线段的关系.
(2)本题运用转化思想,通过全等三角形的性质,可
把线段AB转化成线段DF,再利用等式的性质可把
求线段FB的长转化成求线段AD的长.1如图,△EFG与△NMH全等,在△EFG中,FG是最长的边,在△NMH中,MH是最长的边,∠F和∠M是对应角,且EF=2.4 cm,FH=1.9 cm,HM=3.5 cm.
(1)写出对应相等的边及
对应相等的角;
(2)求线段NM及线段HG
的长度.2若△ABC与△DEF全等,点A和点E,点B和点D分别是对应点,则下列结论错误的是( )
A.BC=EF
B.∠B=∠D
C.∠C=∠F
D.AC=EF3如图,△ABC≌△A′B′C′,则∠C的度数是( )
A.56°
B.51°
C.107°
D.73°找全等三角形的对应元素的方法:
(1)在两个全等三角形中最长边对应最长边,最短边对
应最短边,最大角对应最大角,最小角对应最小角;
(2)对应角的对边为对应边,对应边的对角为对应角;
(3)重合的边(角)一般是对应边(角),公共边(角)一般是
对应边(角),对顶角是对应角.
注意:对应边与对边,对应角与对角不同,对应边和对
应角是相对两个三角形而言的,是两条边、两个角的关
系;而对边与对角则是指一个三角形中的边与角的位置
关系.
全等三角形及其对应元素
全等三角形的性质2课时流程逐点
导讲练课堂小结作业提升 课间操时间,小明和小聪在操场上突然争论起来,
他们都说比对方长得高,这时数学老师走过来,笑着
对他们说:“你们不用争了,比一下你们俩地上的影
子,如果一样长就说明你们一样高.”你知道数学老师
为什么能从他们的影长相等就判
定他们的身高相同吗? 学习了全
等图形的有关知识,我们就可以
说明其中的道理了.1知识点全等图形 我们已经认识了图形的轴对称、平移和旋转,这
是图形的三种基本变换,图形经过这样的变换,位置
发生了改变,但变换前后两个图形的对应线段相等,
对应角相等,图形的形状和大小并没有改变. 要想知道两个图形的形状和大小是否完全相同,
可以通过轴对称、平移和旋转这些图形的变换,把两
个图形叠合在一起,观察它们是否完全重合. 能够完
全重合的两个图形叫做全等图形(congruent figures).1. 定义:能够完全重合的两个图形叫做全等图形.
要点精析:
(1)图形的全等与它们的位置无关,只要满足能够完
全重合即可;而完全重合包含两层含义:图形的
形状相同,大小相等;
(2)全等形的周长、面积分别相等,但周长或面积相
等的两个图形不一定全等.
2. 几种常用全等变换的方式:轴对称、平移、旋转.下图中是全等图形的是_____________________
_____________________.例1(1)和(9)、(2)和(3)、(4)和(8)、(11)和(12)导引:上述图形中,(5)和(7)形状相同,但大小不同,(6)
和(10)形状不同,故都不是全等图形;(1)和(9)、
(2)和(3)、(11)和(12)尽管方向不同,但大小、形
状完全相同,所以它们是全等图形;(4)和(8)都是
五角星,大小、形状都相同,是全等图形.(1)此题运用定义识别全等图形,确定两个图形全等
要符合两个条件:①形状相同,②大小相等;是
不是全等图形与位置无关.
(2)判断两个图形是否全等还可以通过平移、旋转、
翻折等方法把两个图形叠合在一起,看它们能否
重合,即用叠合法判断.1下列各图中,与所给图形全等的是 ( )2下列图形中与已知图形全等的是( )3下列四组图形中,是全等图形的一组是( )2知识点全等三角形及其对应元素 如图中给出了 8个图形,你能发现哪两个图形是
全等图形吗?
动手试试看. 一个图形经过轴对称、平移和旋转等变换所得到
的新图形一定与原图形全等;反过来,两个全等的图
形经过上述变换后一定能够互相重合.
思考:观察图中的
两对多边形,每对
中的其中一个可以
经过怎样的变换和
另一个图形重合? 上面的两对多边形都是全等图形,也称为全等
多边形.两个全等的多边形,经过变换而重合,相互
重合的顶点叫做对应顶点,相互重合的边叫做对应
边,相互重合的角叫做对应角. 如图中的两个五边形是全等的,记作五边形
ABCDE≌五边形A′B′C′D′E′(这里,符号“≌”
表示全等, 读作“全等于”). 点A与点A′、点B与
点B′、点C与点C′、点D与点D′、点E与点E′分别是对应顶点. 依据上面的分析,我们知道:
全等多边形的对应边相等,对应角相等.
这就是全等多边形的性质.实际上,边、角分别
对应相等这两个特征足以刻画多边形的全等了.也就
是说,在数学上我们可以给出全等多边形如下的定
义:
边、角分别对应相等的两个多边形称为全等多
边形.1. 全等三角形的定义:如果两个三角形的边、角分
别对应相等,那么这两个三角形全等.
2. 全等三角形对应元素:把两个全等的三角形重合
到一起,(1)对应顶点:重合的顶点;(2)对应边:
重合的边;(3)对应角:重合的角.3. 全等三角形的表示法:如图,△ABC和△DEF全
等,记作△ABC≌△DEF,符号“≌”读作全等于.
其中“∽”表示形状相同,“=”表示大小相等.记
两个三角形全等时,通常把表示对应顶点的字母
写在对应的位置上,如点A和点D ,点B和点E ,
点C和点F 是对应顶点;AB和DE,BC和EF ,AC
和DF是对应边;∠A和∠D,∠B和∠E ,∠C和
∠F是对应角.4. 对应元素的确定方法:
(1)字母顺序确定法:根据书写规范,按照对应顶点
确定对应边、对应角,如△CAB≌△FDE,则
AB与DE、AC与DF、BC与EF是对应边,∠A和
∠D、∠B和∠E、∠C和∠F是对应角.
(2)图形位置确定法:①公共边一定是对应边;②公
共角一定是对应角;③对顶角一定是对应角.
(3)图形大小确定法:两个全等三角形的最大的边(角)
是对应边(角),最小的边(角)是对应边(角).5. 对应边(或角)与对边(或角)的区别:对应边、对应
角是对两个三角形而言的,指两条边、两个角的
关系;而对边、对角是指一个三角形的边和角的
位置关系. 对边是与角相对的边,对角是与边相对
的角.
6. 易错警示:记两个三角形全等时,通常把表示对
应顶点的字母写在对应的位置上,字母顺序不能
随意书写.如图,△ACB≌△BDA,AC和BD对应,BC和
AD对应,写出其他的对应边及对应角.例2因为已经知道了两组对应边,所以剩下的一组边是
对应边.根据对应边所对的角是对应角,容易发现
AC的对角∠CBA和BD的对角∠DAB是对应角,
BC的对角∠CAB和AD的对角∠DBA是对应角,剩
下的一组角∠ACB和∠BDA是对应角.导引:解:其他的对应边是AB和BA;对应角是∠CBA和
∠DAB,∠CAB和∠DBA,∠ACB和∠BDA. 根根据对应边(角)找对应角(边)的方法:对应边
所对的角是对应角,对应角所对的边是对应边.1如图,△ABC≌△EDC,∠ACB和∠ECD是对应角,BC与DC是对应边,写出其他的对应边及对应角.2如图,沿直线AC对折,△ABC与△ADC重合,则△ABC≌________,AB的对应边是________,∠BCA的对应角是________________.知2-练3如图,将△ABC沿BC所在的直线平移到△A′B′C′
的位置,则△ABC________△A′B′C′,图中∠A与______,∠B与________,∠ACB与_________是
对应角.3知识点全等三角形的性质知3-导 三角形是特殊的多边形,因此,
全等三角形的对应边、对应角分别相等.
同样,我们也可以得到全等三角形的定义,从
而也得到了判断两个三角形是否全等的准确方法:
如果两个三角形的边、角分别对应相等,那么
这两个 三角形全等. 如图所示,△ABC≌△DEF,且∠A=∠D,
∠B=∠E. 你能指出它们之间其他的对应顶点、对应
角和对应边吗?知3-导知3-讲1.性质:全等三角形的对应边相等 ,对应角相等.
要点精析:
(1)全等三角形的对应元素相等.其中,对应元素包
括:对应边、对应角、对应中线、对应高、对应
角平分线、周长、面积等.
(2)在应用全等三角形的性质时,要先确定两个条件:
①两个三角形全等;②找对应元素.
(3)全等三角形的性质是说明线段、角相等的常用
方法.知3-讲2.全等三角形的判定:如果两个三角形的边角分别对
应相等,那么这两个三角形全等.
3.易错警示:周长相等的两个三角形不一定全等,面
积相等的两个三角形也不一定全等.知3-讲如图,△ABC沿着BC的方向平移至△DEF,∠A=80°,∠B=60°,求∠F的度数.例3知3-讲解:由图形平移的特征,可知与△ABC与△DEF的形状
与大小相同,即
△ABC≌△DEF.
∴ ∠D=∠A=80°(全等三角形的对应角相等).
同理∠DEF=∠B=60°.
又∵∠D+∠DEF+∠F = 180°(三角形的内角和
等于180°),
∴∠F=180°-∠D-∠DEF
=180°-80°-60°=40°.(1)全等三角形的性质在几何计算中起着重要作用,
当所求线段不是全等三角形的对应边时,可利用
等式的性质进行转换,从而找到所求线段与已知
线段的关系.
(2)本题运用转化思想,通过全等三角形的性质,可
把线段AB转化成线段DF,再利用等式的性质可把
求线段FB的长转化成求线段AD的长.1如图,△EFG与△NMH全等,在△EFG中,FG是最长的边,在△NMH中,MH是最长的边,∠F和∠M是对应角,且EF=2.4 cm,FH=1.9 cm,HM=3.5 cm.
(1)写出对应相等的边及
对应相等的角;
(2)求线段NM及线段HG
的长度.2若△ABC与△DEF全等,点A和点E,点B和点D分别是对应点,则下列结论错误的是( )
A.BC=EF
B.∠B=∠D
C.∠C=∠F
D.AC=EF3如图,△ABC≌△A′B′C′,则∠C的度数是( )
A.56°
B.51°
C.107°
D.73°找全等三角形的对应元素的方法:
(1)在两个全等三角形中最长边对应最长边,最短边对
应最短边,最大角对应最大角,最小角对应最小角;
(2)对应角的对边为对应边,对应边的对角为对应角;
(3)重合的边(角)一般是对应边(角),公共边(角)一般是
对应边(角),对顶角是对应角.
注意:对应边与对边,对应角与对角不同,对应边和对
应角是相对两个三角形而言的,是两条边、两个角的关
系;而对边与对角则是指一个三角形中的边与角的位置
关系.
