10.3.2 旋转的特征 课件(17张PPT)
文档属性
| 名称 | 10.3.2 旋转的特征 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 750.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 10:33:00 | ||
图片预览


文档简介
课件17张PPT。10.3 旋转
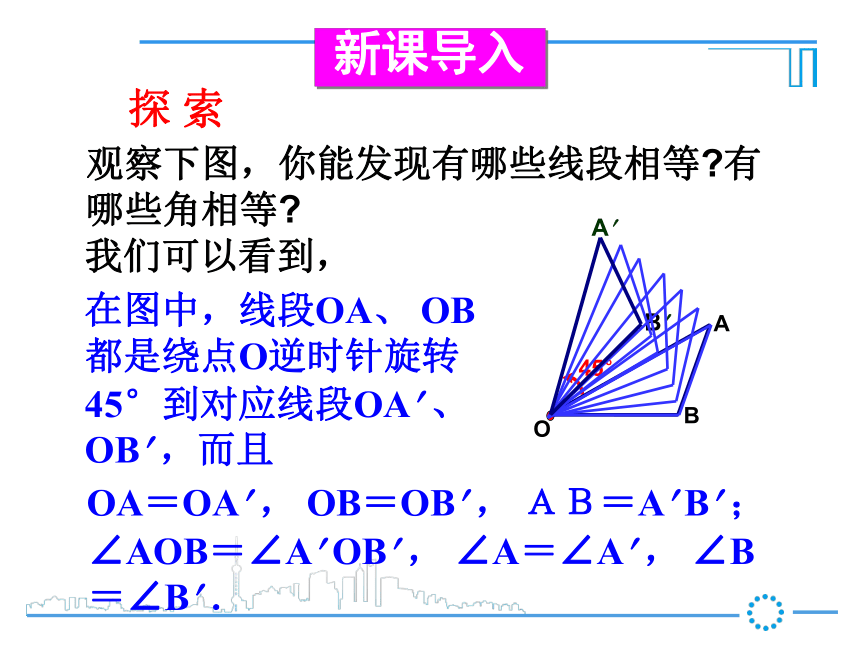
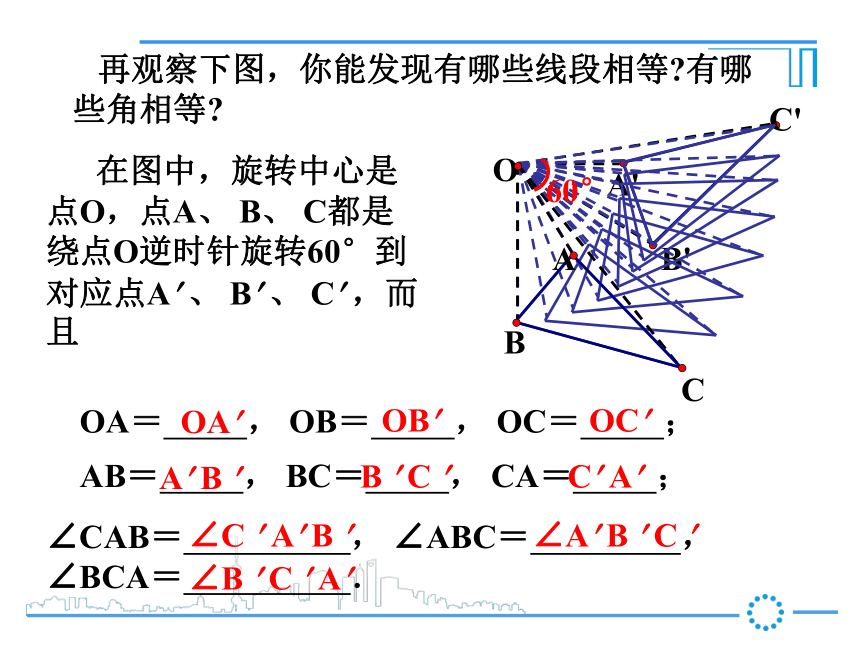
2. 旋转的特征探 索观察下图,你能发现有哪些线段相等?有哪些角相等?在图中,线段OA、 OB都是绕点O逆时针旋转45°到对应线段OA? 、 OB? ,而且45°A? B? 我们可以看到,OA=OA? , OB=OB? , AB=A? B? ;∠AOB=∠A? OB? , ∠A=∠A? , ∠B=∠B? .新课导入 在图中,旋转中心是点O,点A、 B、 C都是绕点O逆时针旋转60°到对应点A? 、 B? 、 C? ,而且 再观察下图,你能发现有哪些线段相等?有哪些角相等?O60°OA= , OB= , OC= ;AB= , BC= , CA= ;∠CAB= , ∠ABC= , ∠BCA= .OA?OB?OC?A? B ? B ? C ? C? A? ∠C ? A? B ? ∠A? B ? C ? ∠B ? C ? A? 旋转的基本性质(1)旋转不改变图形的形状和大小.
(2)图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度.
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.
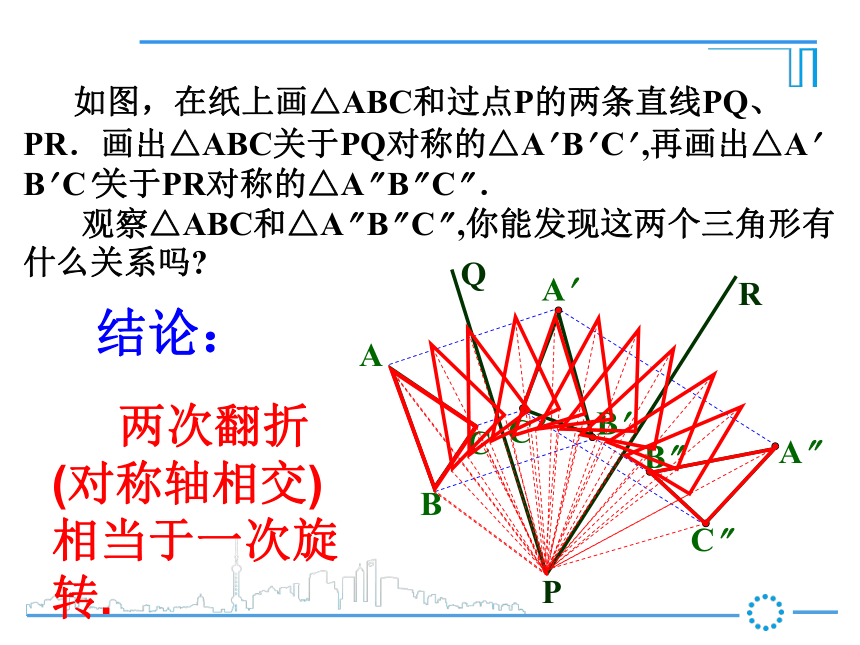
(5)对应线段相等,对应角相等.新课推进C? ABCA? B? A? B? C? 如图,在纸上画△ABC和过点P的两条直线PQ、PR.画出△ABC关于PQ对称的△A? B? C? ,再画出△A? B? C?关于PR对称的△A? B? C? .
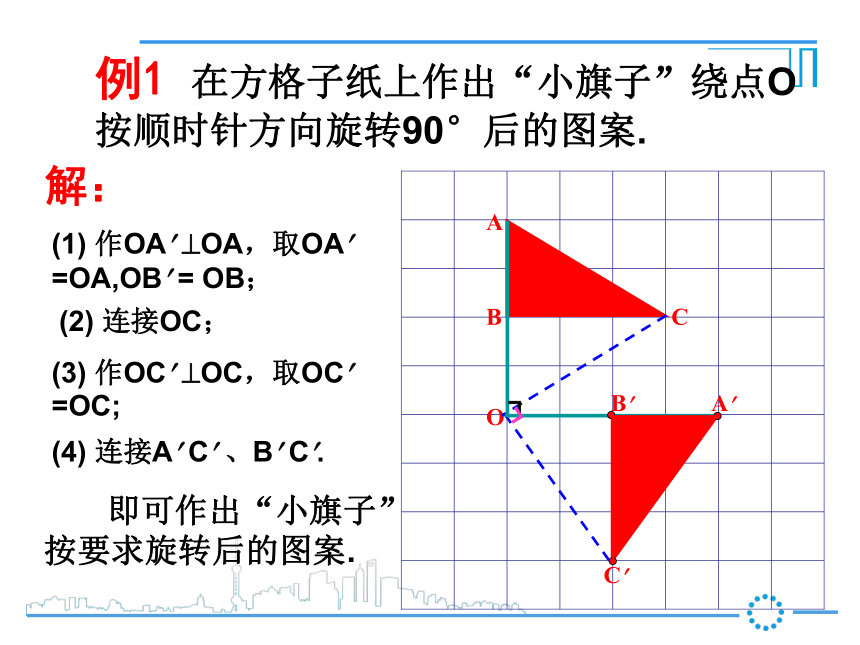
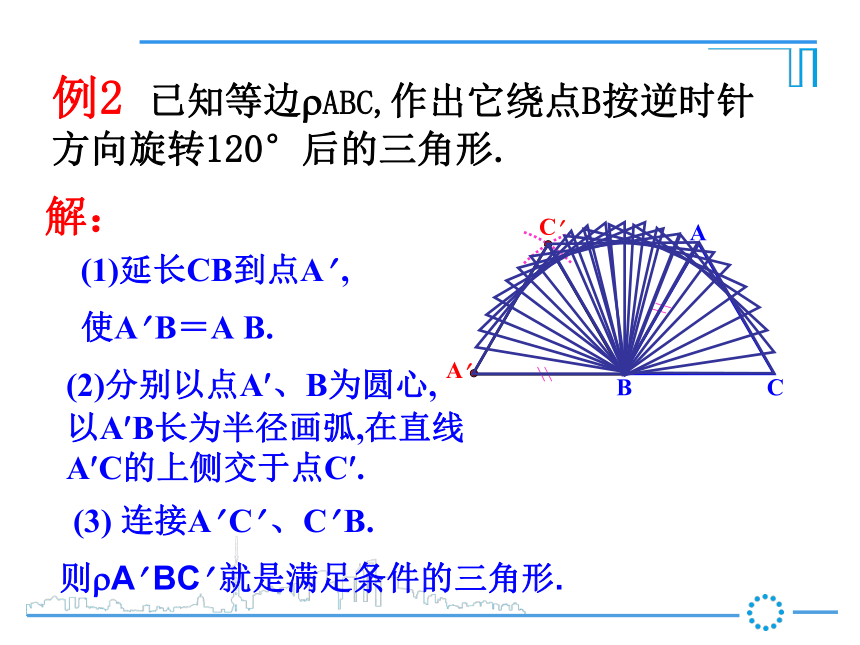
观察△ABC和△A? B? C? ,你能发现这两个三角形有什么关系吗?结论: 两次翻折(对称轴相交)相当于一次旋转.A? B? C? 例1 在方格子纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案.(1) 作OA? ?OA,取OA? =OA,OB? = OB;(2) 连接OC;(3) 作OC? ?OC,取OC? =OC;(4) 连接A? C? 、B? C?.┓┓ 即可作出“小旗子”按要求旋转后的图案.解:例2 已知等边?ABC,作出它绕点B按逆时针方向旋转120°后的三角形.A? C? ABC解:(1)延长CB到点A? ,(2)分别以点A?、B为圆心,(3) 连接A? C? 、C? B.则?A? BC? 就是满足条件的三角形.使A? B=A B.以A?B长为半径画弧,在直线A?C的上侧交于点C?.例3 如图,在正方形ABCD中, ?ABE旋转后能与?ADF重合O(1)旋转中心是哪一点?(2)旋转了多少度?(3)线段AF与BE的位置关系如何?如何找旋转中心呢?旋转中心在对应点连线的垂直平分线上,你知道为什么吗?怎样画一个图形关于一个点旋转后的图形?如何来确定旋转中心?主要是画图形上的几个点旋转后的对应点.用对称点连线的中垂线来确定.1.如图所示, △ABO绕点O旋转得到△CDO,在这个旋转过程中:(1) 旋转中心( ),旋转角是( ).(2)经过旋转,点A、B分别移到了( ).(3)若AO=3cm,则CO=( ).(4) 若∠AOC=60°,∠AOD=20°,则∠BOD=( ),
∠DOC=( ).课堂演练O∠BODC、D3cm60°40°2. 如图,四边形ABCD与四边形EFGO都是边长相等的的正方形,对角线AC与BD交于点O,那么正方形EFGO绕点O无论怎样转动,请你猜想,两个正方形重叠部分的面积会是一个正方形面积的多少?你能否用旋转有关知识说明理由.ABCDOEFGKH 利用图形的旋转可以使分散的条件与结论相对地集中,以便发现条件与结论之间的关系,从而获得问题解决的思路与途径。3.在正方形ABCD中, ∠1=∠2 =30°.试把ΔADE绕点A顺时针旋转90°,观察整个图形中角与角之间,线段与线段之间,存在哪些相等关系?探索DE,BF,AF之间的关系. 4. 如图,正方形ABCD的边长为1, AB、AD上各有一点P、Q,如果三角形APQ的周长为2,求∠PCQ。如图,把ΔDQC逆时针方向旋转90°到ΔBEC
则DQ=BE,CQ=CE。有QP=2-AQ-AP,
EP=BP+BE=BP+DQ= (1-AP) + (1-AQ) =QP
所以ΔQCP≌ΔECP(SSS)所以∠PCQ= ∠PCE=45 °*解决问题A?B?如图,河两边有A、B两个村庄,现准备建一座桥,桥必须与河岸垂直,问桥应建在何处才能使由甲到乙的路程最短?请作出图形,并说说理由.CED 通过这节课的学习活动,你有什么收获?课堂小结1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业谁在装束和发型上用尽心思,谁就没有精力用于学习;谁只注意修饰外表的美丽,谁就无法得到内在的美丽。 —— 杨尊田
2. 旋转的特征探 索观察下图,你能发现有哪些线段相等?有哪些角相等?在图中,线段OA、 OB都是绕点O逆时针旋转45°到对应线段OA? 、 OB? ,而且45°A? B? 我们可以看到,OA=OA? , OB=OB? , AB=A? B? ;∠AOB=∠A? OB? , ∠A=∠A? , ∠B=∠B? .新课导入 在图中,旋转中心是点O,点A、 B、 C都是绕点O逆时针旋转60°到对应点A? 、 B? 、 C? ,而且 再观察下图,你能发现有哪些线段相等?有哪些角相等?O60°OA= , OB= , OC= ;AB= , BC= , CA= ;∠CAB= , ∠ABC= , ∠BCA= .OA?OB?OC?A? B ? B ? C ? C? A? ∠C ? A? B ? ∠A? B ? C ? ∠B ? C ? A? 旋转的基本性质(1)旋转不改变图形的形状和大小.
(2)图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度.
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.
(5)对应线段相等,对应角相等.新课推进C? ABCA? B? A? B? C? 如图,在纸上画△ABC和过点P的两条直线PQ、PR.画出△ABC关于PQ对称的△A? B? C? ,再画出△A? B? C?关于PR对称的△A? B? C? .
观察△ABC和△A? B? C? ,你能发现这两个三角形有什么关系吗?结论: 两次翻折(对称轴相交)相当于一次旋转.A? B? C? 例1 在方格子纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案.(1) 作OA? ?OA,取OA? =OA,OB? = OB;(2) 连接OC;(3) 作OC? ?OC,取OC? =OC;(4) 连接A? C? 、B? C?.┓┓ 即可作出“小旗子”按要求旋转后的图案.解:例2 已知等边?ABC,作出它绕点B按逆时针方向旋转120°后的三角形.A? C? ABC解:(1)延长CB到点A? ,(2)分别以点A?、B为圆心,(3) 连接A? C? 、C? B.则?A? BC? 就是满足条件的三角形.使A? B=A B.以A?B长为半径画弧,在直线A?C的上侧交于点C?.例3 如图,在正方形ABCD中, ?ABE旋转后能与?ADF重合O(1)旋转中心是哪一点?(2)旋转了多少度?(3)线段AF与BE的位置关系如何?如何找旋转中心呢?旋转中心在对应点连线的垂直平分线上,你知道为什么吗?怎样画一个图形关于一个点旋转后的图形?如何来确定旋转中心?主要是画图形上的几个点旋转后的对应点.用对称点连线的中垂线来确定.1.如图所示, △ABO绕点O旋转得到△CDO,在这个旋转过程中:(1) 旋转中心( ),旋转角是( ).(2)经过旋转,点A、B分别移到了( ).(3)若AO=3cm,则CO=( ).(4) 若∠AOC=60°,∠AOD=20°,则∠BOD=( ),
∠DOC=( ).课堂演练O∠BODC、D3cm60°40°2. 如图,四边形ABCD与四边形EFGO都是边长相等的的正方形,对角线AC与BD交于点O,那么正方形EFGO绕点O无论怎样转动,请你猜想,两个正方形重叠部分的面积会是一个正方形面积的多少?你能否用旋转有关知识说明理由.ABCDOEFGKH 利用图形的旋转可以使分散的条件与结论相对地集中,以便发现条件与结论之间的关系,从而获得问题解决的思路与途径。3.在正方形ABCD中, ∠1=∠2 =30°.试把ΔADE绕点A顺时针旋转90°,观察整个图形中角与角之间,线段与线段之间,存在哪些相等关系?探索DE,BF,AF之间的关系. 4. 如图,正方形ABCD的边长为1, AB、AD上各有一点P、Q,如果三角形APQ的周长为2,求∠PCQ。如图,把ΔDQC逆时针方向旋转90°到ΔBEC
则DQ=BE,CQ=CE。有QP=2-AQ-AP,
EP=BP+BE=BP+DQ= (1-AP) + (1-AQ) =QP
所以ΔQCP≌ΔECP(SSS)所以∠PCQ= ∠PCE=45 °*解决问题A?B?如图,河两边有A、B两个村庄,现准备建一座桥,桥必须与河岸垂直,问桥应建在何处才能使由甲到乙的路程最短?请作出图形,并说说理由.CED 通过这节课的学习活动,你有什么收获?课堂小结1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业谁在装束和发型上用尽心思,谁就没有精力用于学习;谁只注意修饰外表的美丽,谁就无法得到内在的美丽。 —— 杨尊田
