2020版高中数学新人教B版必修5课件:第一章解三角形1.1.2余弦定理(二)(28张PPT)
文档属性
| 名称 | 2020版高中数学新人教B版必修5课件:第一章解三角形1.1.2余弦定理(二)(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 852.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 00:00:00 | ||
图片预览








文档简介
课件28张PPT。1.1.2 余弦定理(二)[学习目标]
1.熟练掌握余弦定理及其变形形式.
2.会用余弦定理解三角形.
3.能利用正、余弦定理解决三角形的有关问题.[知识链接]
1.以下问题不能用余弦定理求解的是 .
(1)已知两边和其中一边的对角,解三角形.
(2)已知两角和一边,求其他角和边.
(3)已知一个三角形的两条边及其夹角,求其他的边和角.
(4)已知一个三角形的三条边,解三角形.(2)2.利用余弦定理判断三角形的形状,正确的是 .
(1)在△ABC中,若a2=b2+c2,则△ABC为直角三角形.
(2)在△ABC中,若a2(3)在△ABC中,若a2>b2+c2,则△ABC为钝角三角形.(1)(3)[预习导引]
1.正弦定理及其变形
(1) = (R为△ABC外接圆半径).
(2)a= ,b= ,c= .
2.余弦定理及其推论
(1)a2= ,b2= ,c2=
.a2+b2-2abcos C2R2Rsin A2Rsin B2Rsin Cb2+c2-2bccos Ac2+a2-2cacos B(2)cos A= ,cos B= ,cos C= .
(3)在△ABC中,c2=a2+b2?C为 ;c2>a2+b2?C为 ;c23.三角变换公式
(1)cos(α+β)= .
(2)cos(α-β)= .
(3)cos2α= = = . cos αcos β-sin αsin β
cos αcos β+sin αsin β
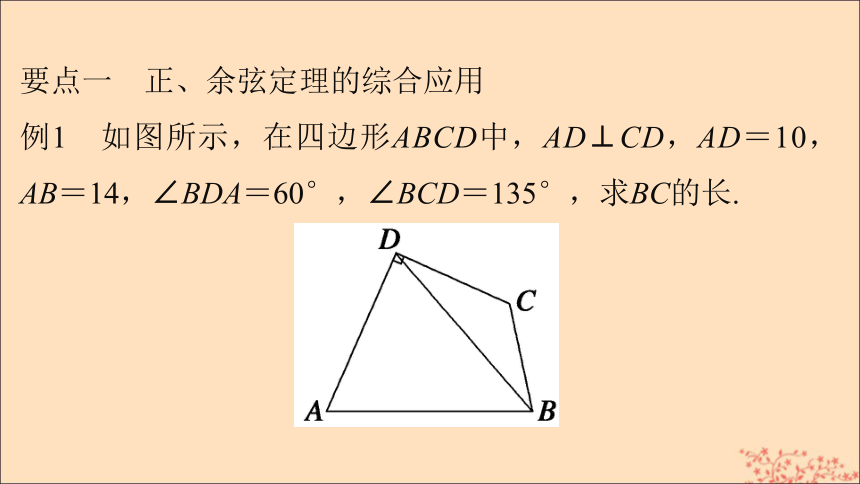
cos2α-sin2α 2cos2α-1 1-2sin2α直角钝角锐角要点一 正、余弦定理的综合应用
例1 如图所示,在四边形ABCD中,AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,求BC的长.解 在△ABD中,AD=10,AB=14,∠BDA=60°,设BD=x,
由余弦定理,得AB2=AD2+BD2-2AD·BDcos∠BDA,
∴142=102+x2-2×10·xcos 60°,
即x2-10x-96=0,解得x1=16,x2=-6(舍去),
∴BD=16.
∵AD⊥CD,∠BDA=60°,∴∠CDB=30°.在△BCD中,由正弦定理:规律方法 余弦定理和正弦定理一样,都是围绕着三角形进行边角互换的.在有关三角形的题目中注意选择是应用正弦定理,还是余弦定理,必要时也可列方程(组)求解.同时,要有意识地考虑用哪个定理更合适,或是两个定理都要用,要抓住能利用某个定理的信息.跟踪演练1 在△ABC中,内角A,B,C的对边长分别为a,b,c,已知a2-c2=2b,且sin Acos C=3cos Asin C,求b.解 方法一 在△ABC中,∵sin Acos C=3cos Asin C,
则由正弦定理及余弦定理有:
化简并整理得:
2(a2-c2)=b2.
又由已知a2-c2=2b,∴4b=b2.解得b=4或b=0(舍).方法二 由余弦定理得:a2-c2=b2-2bccos A.
又a2-c2=2b,b≠0.所以b=2ccos A+2. ①
又sin Acos C=3cos Asin C,
∴sin Acos C+cos Asin C=4cos Asin C,
sin(A+C)=4cos Asin C,
即sin B=4cos Asin C,
由正弦定理得sin B= sin C,故b=4ccos A. ②
由①②解得b=4.要点二 利用正、余弦定理证明三角形中的恒等式
例2 在△ABC中,有:
(1)a=bcos C+ccos B;
(2)b=ccos A+acos C;
(3)c=acos B+bcos A;
这三个关系式也称为射影定理,请给出证明.证明 方法一 (1)设△ABC外接圆半径为R,
由正弦定理得b=2Rsin B,c=2Rsin C,
∴bcos C+ccos B=2Rsin Bcos C+2Rsin Ccos B
=2R(sin Bcos C+cos Bsin C)
=2Rsin(B+C)=2Rsin A=a.
即a=bcos C+ccos B
同理可证(2)b=ccos A+acos C;
(3)c=acos B+bcos A.方法二 (1)由余弦定理得
∴a=bcos C+ccos B.
同理可证(2)b=ccos A+acos C;
(3)c=acos B+bcos A.规律方法 (1)证明三角恒等式的关键是消除等号两端
三角函数式的差异.形式上一般有:左?右;右?左或左
?中?右三种.
(2)利用正、余弦定理证明三角形中的恒等式的途径有
两种途径:一是把角的关系通过正、余弦定理转化为边
的关系;二是把边的关系转化为角的关系,一般是通过
正弦定理转化.跟踪演练2 在△ABC中,a、b、c分别是角A、B、C的对边,求证:
证明 方法一 因为左边=
∴等式成立.方法二 设△ABC外接圆半径为R,
∵右边=
∴等式成立.要点三 利用正、余弦定理判断三角形形状
例3 在△ABC中,已知(a+b+c)(b+c-a)=3bc,且sin A=2sin Bcos C,试确定△ABC的形状.解 由(a+b+c)(b+c-a)=3bc,
得b2+2bc+c2-a2=3bc,
即a2=b2+c2-bc,又A∈(0,π),∴A= ,
又sin A=2sin Bcos C,
由正、余弦定理,得a=2b·
∴b2=c2,b=c,∴△ABC为等边三角形.规律方法 题中边的大小没有明确给出,而是通过一个关系式来确定的,可以考虑利用正弦定理将边的关系转化为角的关系,也可以利用余弦定理将边、角关系转化为边的关系来判断.跟踪演练3 在△ABC中,若B=60°,2b=a+c,试判断△ABC的形状.
解 方法一 根据余弦定理得
b2=a2+c2-2accos B.∵B=60°,2b=a+c,
∴ =a2+c2-2accos 60°,
整理得(a-c)2=0,∴a=c.
又∵2b=a+c,∴2b=2a,即b=a.
∴△ABC是等边三角形.方法二 根据正弦定理,
2b=a+c可转化为2sin B=sin A+sin C.
又∵B=60°,∴A+C=120°.∴C=120°-A,
∴2sin 60°=sin A+sin(120°-A),
整理得sin(A+30°)=1,
∴A=60°,C=60°.
∴△ABC是等边三角形.1.在△ABC中,sin A∶sin B∶sin C=3∶2∶3,则cos C的值为 ( )
解析 根据正弦定理, a∶b∶c=sin A∶sin B∶sin C=3∶2∶3,设a=3k,b=2k,c=3k(k>0).
则有cos C=A当堂检测2.在△ABC中,若2cos Bsin A=sin C,则△ABC的形状一定是( )
A.等腰直角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
解析 ∵2cos Bsin A=sin C,∴2× ×a=c,
∴a=b.故△ABC为等腰三角形.C3.在△ABC中,若a2+c2-b2= ac,则角B的值为 .
解析 根据余弦定理,cos B= ,又B∈(0,π),所以B= .4.在△ABC中,若B=30°,AB=2 ,AC=2,则满足条件的三角形有几个?
解 设BC=a,AC=b,AB=c,
由余弦定理,得b2=a2+c2-2accos B,
∴22=a2+(2 )2-2a×2 cos 30°,即a2-6a+8=0,解得a=2或a=4.
当a=2时,三边为2,2,2 可组成三角形;
当a=4时,三边为4,2,2 也可组成三角形.
∴满足条件的三角形有两个.课堂小结
1.已知两边及其中一边的对角,解三角形,一般情况下,利用正弦定理求出另一边所对的角,再求其他的边或角,要注意进行讨论.如果采用余弦定理来解,只需解一个一元二次方程,即可求出边来,比较两种方法,采用余弦定理较简单.
2.根据所给条件确定三角形的形状,主要有两种途径
(1)化边为角,并利用三角恒等变形进行化简;
(2)化角为边,并常用正弦(余弦)定理实施边、角转换. 3.在余弦定理中,每一个等式均含有四个量,利用方程的观点,可以知三求一.
4.利用余弦定理求三角形的边长时容易出现增解,原因是余弦定理中涉及的是边长的平方,通常转化为一元二次方程求正实数.因此解题时需特别注意三角形三边长度所应满足的基本条件.
1.熟练掌握余弦定理及其变形形式.
2.会用余弦定理解三角形.
3.能利用正、余弦定理解决三角形的有关问题.[知识链接]
1.以下问题不能用余弦定理求解的是 .
(1)已知两边和其中一边的对角,解三角形.
(2)已知两角和一边,求其他角和边.
(3)已知一个三角形的两条边及其夹角,求其他的边和角.
(4)已知一个三角形的三条边,解三角形.(2)2.利用余弦定理判断三角形的形状,正确的是 .
(1)在△ABC中,若a2=b2+c2,则△ABC为直角三角形.
(2)在△ABC中,若a2
1.正弦定理及其变形
(1) = (R为△ABC外接圆半径).
(2)a= ,b= ,c= .
2.余弦定理及其推论
(1)a2= ,b2= ,c2=
.a2+b2-2abcos C2R2Rsin A2Rsin B2Rsin Cb2+c2-2bccos Ac2+a2-2cacos B(2)cos A= ,cos B= ,cos C= .
(3)在△ABC中,c2=a2+b2?C为 ;c2>a2+b2?C为 ;c2
(1)cos(α+β)= .
(2)cos(α-β)= .
(3)cos2α= = = . cos αcos β-sin αsin β
cos αcos β+sin αsin β
cos2α-sin2α 2cos2α-1 1-2sin2α直角钝角锐角要点一 正、余弦定理的综合应用
例1 如图所示,在四边形ABCD中,AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,求BC的长.解 在△ABD中,AD=10,AB=14,∠BDA=60°,设BD=x,
由余弦定理,得AB2=AD2+BD2-2AD·BDcos∠BDA,
∴142=102+x2-2×10·xcos 60°,
即x2-10x-96=0,解得x1=16,x2=-6(舍去),
∴BD=16.
∵AD⊥CD,∠BDA=60°,∴∠CDB=30°.在△BCD中,由正弦定理:规律方法 余弦定理和正弦定理一样,都是围绕着三角形进行边角互换的.在有关三角形的题目中注意选择是应用正弦定理,还是余弦定理,必要时也可列方程(组)求解.同时,要有意识地考虑用哪个定理更合适,或是两个定理都要用,要抓住能利用某个定理的信息.跟踪演练1 在△ABC中,内角A,B,C的对边长分别为a,b,c,已知a2-c2=2b,且sin Acos C=3cos Asin C,求b.解 方法一 在△ABC中,∵sin Acos C=3cos Asin C,
则由正弦定理及余弦定理有:
化简并整理得:
2(a2-c2)=b2.
又由已知a2-c2=2b,∴4b=b2.解得b=4或b=0(舍).方法二 由余弦定理得:a2-c2=b2-2bccos A.
又a2-c2=2b,b≠0.所以b=2ccos A+2. ①
又sin Acos C=3cos Asin C,
∴sin Acos C+cos Asin C=4cos Asin C,
sin(A+C)=4cos Asin C,
即sin B=4cos Asin C,
由正弦定理得sin B= sin C,故b=4ccos A. ②
由①②解得b=4.要点二 利用正、余弦定理证明三角形中的恒等式
例2 在△ABC中,有:
(1)a=bcos C+ccos B;
(2)b=ccos A+acos C;
(3)c=acos B+bcos A;
这三个关系式也称为射影定理,请给出证明.证明 方法一 (1)设△ABC外接圆半径为R,
由正弦定理得b=2Rsin B,c=2Rsin C,
∴bcos C+ccos B=2Rsin Bcos C+2Rsin Ccos B
=2R(sin Bcos C+cos Bsin C)
=2Rsin(B+C)=2Rsin A=a.
即a=bcos C+ccos B
同理可证(2)b=ccos A+acos C;
(3)c=acos B+bcos A.方法二 (1)由余弦定理得
∴a=bcos C+ccos B.
同理可证(2)b=ccos A+acos C;
(3)c=acos B+bcos A.规律方法 (1)证明三角恒等式的关键是消除等号两端
三角函数式的差异.形式上一般有:左?右;右?左或左
?中?右三种.
(2)利用正、余弦定理证明三角形中的恒等式的途径有
两种途径:一是把角的关系通过正、余弦定理转化为边
的关系;二是把边的关系转化为角的关系,一般是通过
正弦定理转化.跟踪演练2 在△ABC中,a、b、c分别是角A、B、C的对边,求证:
证明 方法一 因为左边=
∴等式成立.方法二 设△ABC外接圆半径为R,
∵右边=
∴等式成立.要点三 利用正、余弦定理判断三角形形状
例3 在△ABC中,已知(a+b+c)(b+c-a)=3bc,且sin A=2sin Bcos C,试确定△ABC的形状.解 由(a+b+c)(b+c-a)=3bc,
得b2+2bc+c2-a2=3bc,
即a2=b2+c2-bc,又A∈(0,π),∴A= ,
又sin A=2sin Bcos C,
由正、余弦定理,得a=2b·
∴b2=c2,b=c,∴△ABC为等边三角形.规律方法 题中边的大小没有明确给出,而是通过一个关系式来确定的,可以考虑利用正弦定理将边的关系转化为角的关系,也可以利用余弦定理将边、角关系转化为边的关系来判断.跟踪演练3 在△ABC中,若B=60°,2b=a+c,试判断△ABC的形状.
解 方法一 根据余弦定理得
b2=a2+c2-2accos B.∵B=60°,2b=a+c,
∴ =a2+c2-2accos 60°,
整理得(a-c)2=0,∴a=c.
又∵2b=a+c,∴2b=2a,即b=a.
∴△ABC是等边三角形.方法二 根据正弦定理,
2b=a+c可转化为2sin B=sin A+sin C.
又∵B=60°,∴A+C=120°.∴C=120°-A,
∴2sin 60°=sin A+sin(120°-A),
整理得sin(A+30°)=1,
∴A=60°,C=60°.
∴△ABC是等边三角形.1.在△ABC中,sin A∶sin B∶sin C=3∶2∶3,则cos C的值为 ( )
解析 根据正弦定理, a∶b∶c=sin A∶sin B∶sin C=3∶2∶3,设a=3k,b=2k,c=3k(k>0).
则有cos C=A当堂检测2.在△ABC中,若2cos Bsin A=sin C,则△ABC的形状一定是( )
A.等腰直角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
解析 ∵2cos Bsin A=sin C,∴2× ×a=c,
∴a=b.故△ABC为等腰三角形.C3.在△ABC中,若a2+c2-b2= ac,则角B的值为 .
解析 根据余弦定理,cos B= ,又B∈(0,π),所以B= .4.在△ABC中,若B=30°,AB=2 ,AC=2,则满足条件的三角形有几个?
解 设BC=a,AC=b,AB=c,
由余弦定理,得b2=a2+c2-2accos B,
∴22=a2+(2 )2-2a×2 cos 30°,即a2-6a+8=0,解得a=2或a=4.
当a=2时,三边为2,2,2 可组成三角形;
当a=4时,三边为4,2,2 也可组成三角形.
∴满足条件的三角形有两个.课堂小结
1.已知两边及其中一边的对角,解三角形,一般情况下,利用正弦定理求出另一边所对的角,再求其他的边或角,要注意进行讨论.如果采用余弦定理来解,只需解一个一元二次方程,即可求出边来,比较两种方法,采用余弦定理较简单.
2.根据所给条件确定三角形的形状,主要有两种途径
(1)化边为角,并利用三角恒等变形进行化简;
(2)化角为边,并常用正弦(余弦)定理实施边、角转换. 3.在余弦定理中,每一个等式均含有四个量,利用方程的观点,可以知三求一.
4.利用余弦定理求三角形的边长时容易出现增解,原因是余弦定理中涉及的是边长的平方,通常转化为一元二次方程求正实数.因此解题时需特别注意三角形三边长度所应满足的基本条件.
