2018-2019学年江西省赣州市十五县(市)高二(下)期中数学试卷(文科)解析版
文档属性
| 名称 | 2018-2019学年江西省赣州市十五县(市)高二(下)期中数学试卷(文科)解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 118.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 15:10:10 | ||
图片预览



文档简介
2018-2019学年江西省赣州市十五县(市)高二(下)期中数学试卷(文科)
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.复数z=﹣2+i,则它的共轭复数在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.设a,b是实数,则“a+b>0”是“ab>0”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.用反证法证明命题“三角形中最多只有一个内角是钝角”时,结论的否定是( )
A.没有一个内角是钝角 B.有两个内角是钝角
C.有三个内角是钝角 D.至少有两个内角是钝角
4.某镇有A.B.C三个村,它们的精准扶贫的人口数量之比为3:4:5,现在用分层抽样的方法抽出容量为n的样本,样本中A村有15人,则样本容量为( )
A.50 B.60 C.70 D.80
5.某产品的广告费用x与销售额y的统计数据如表:
广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程=x+中的为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.67.7万元 C.65.5万元 D.72.0万元
6.一组数据中的每一个数据都减去80,得一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( )
A.81.2,4.4 B.78.8,4.4 C.81.2,84.4 D.78.8,75.6
7.已知点P(﹣1,4),过点P恰存在两条直线与抛物线C有且只有一个公共点,则抛物线C的标准方程为( )
A.x2= B.x2=4y或y2=﹣16x
C.y2=﹣16x D.x2=y或y2=﹣16x
8.如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
A. B. C. D.
9.《孙子算经》是中国古代重要的数学著作,书中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?“该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚减一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解,如图是解决这类问题的程序框图,若输入n=24,则输出的结果为( )
A.23 B.47 C.24 D.48
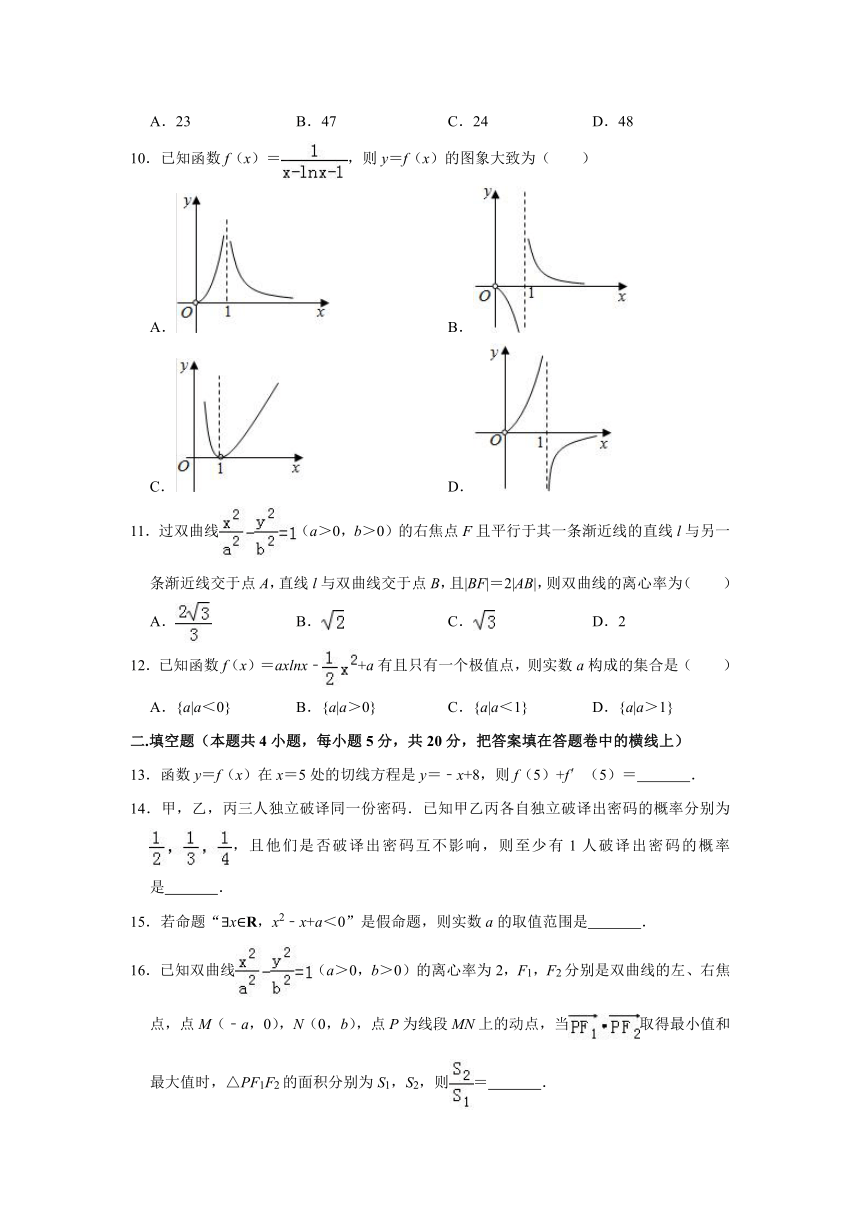
10.已知函数f(x)=,则y=f(x)的图象大致为( )
A. B.
C. D.
11.过双曲线(a>0,b>0)的右焦点F且平行于其一条渐近线的直线l与另一条渐近线交于点A,直线l与双曲线交于点B,且|BF|=2|AB|,则双曲线的离心率为( )
A. B. C. D.2
12.已知函数f(x)=axlnx﹣+a有且只有一个极值点,则实数a构成的集合是( )
A.{a|a<0} B.{a|a>0} C.{a|a<1} D.{a|a>1}
二.填空题(本题共4小题,每小题5分,共20分,把答案填在答题卷中的横线上)
13.函数y=f(x)在x=5处的切线方程是y=﹣x+8,则f(5)+f′(5)= .
14.甲,乙,丙三人独立破译同一份密码.已知甲乙丙各自独立破译出密码的概率分别为,且他们是否破译出密码互不影响,则至少有1人破译出密码的概率是 .
15.若命题“?x∈R,x2﹣x+a<0”是假命题,则实数a的取值范围是 .
16.已知双曲线(a>0,b>0)的离心率为2,F1,F2分别是双曲线的左、右焦点,点M(﹣a,0),N(0,b),点P为线段MN上的动点,当取得最小值和最大值时,△PF1F2的面积分别为S1,S2,则= .
三、解答题(本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(12分)一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同,随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.
(1)求“抽取的卡片上的数字满足a+b=c”的概率;
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
(注:若三个数a,b,c满足a≤b≤c,则称b为这三个数的中位数)
18.(12分)已经集合A={x|﹣1<x<7},B={x|2﹣m≤x≤3m+1},设命题p:满足A∩B=B,命题q:只有一个实数x满足不等式x2+2mx+2m≤0,若命题“p或q”是假命题,求m的取值范围.
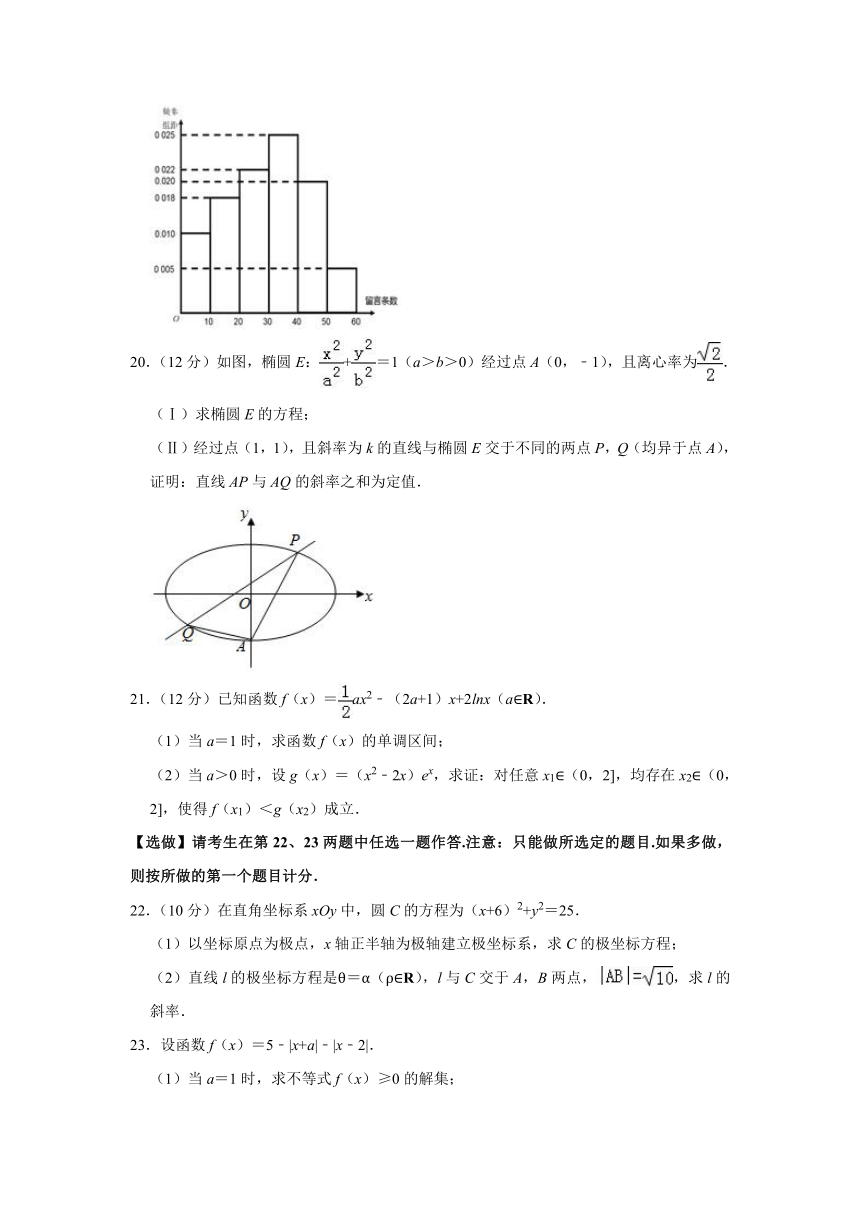
19.(12分)2018年11月21日,意大利奢侈品牌“D&G”在广告中涉嫌辱华,中国明星纷纷站出来抵制该品牌,随后京东、天猫、唯品会等中国电商平台全线下架了该品牌商品,当天有大量网友关注此事件,某网上论坛从关注此事件跟帖中,随机抽取了100名网友进行调查统计,先分别统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到如图所示的频率分布直方图;并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计得到列联表的部分数据如表.
(1)根据如图所示的频率分布直方图,求网友留言条数的中位数;
(2)在答题卡上补全2×2列联表中数据;
(3)判断能否有95%的把握认为网友对此事件是否为“强烈关注”与性别有关?
一般关注
强烈关注
合计
男
45
女
10
55
合计
100
参考公式及数据:
P(K2≥K0)
0.05
0.025
0.010
0.005
k0
3.841
5.024
6.635
7.879
20.(12分)如图,椭圆E:+=1(a>b>0)经过点A(0,﹣1),且离心率为.
(Ⅰ)求椭圆E的方程;
(Ⅱ)经过点(1,1),且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为定值.
21.(12分)已知函数f(x)=ax2﹣(2a+1)x+2lnx(a∈R).
(1)当a=1时,求函数f(x)的单调区间;
(2)当a>0时,设g(x)=(x2﹣2x)ex,求证:对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2)成立.
【选做】请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
22.(10分)在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.
(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;
(2)直线l的极坐标方程是θ=α(ρ∈R),l与C交于A,B两点,,求l的斜率.
23.设函数f(x)=5﹣|x+a|﹣|x﹣2|.
(1)当a=1时,求不等式f(x)≥0的解集;
(2)若f(x)≤1,求a的取值范围.
2018-2019学年江西省赣州市十五县(市)高二(下)期中数学试卷(文科)
参考答案与试题解析
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.【解答】解:∵z=﹣2+i,
∴它的共轭复数=﹣2﹣i,对应的坐标为(﹣2,﹣1)位于第三象限,
故选:C.
2.【解答】解:a,b是实数,如果a=﹣1,b=2则“a+b>0”,则“ab>0”不成立.
如果a=﹣1,b=﹣2,ab>0,但是a+b>0不成立,
所以设a,b是实数,则“a+b>0”是“ab>0”的既不充分也不必要条件.
故选:D.
3.【解答】解:命题“三角形中最多只有一个内角是钝角”的结论的否定是“至少有两个内角是钝角”
故选:D.
4.【解答】解:A村所占的比例为=,
15÷=60,故样本容量n=60,
故选:B.
5.【解答】解:由表中数据得:=3.5,==42,
又回归方程=x+中的为9.4,
故=42﹣9.4×3.5=9.1,
∴=9.4x+9.1.
将x=6代入回归直线方程,得y=9.4×6+9.1=65.5(万元).
∴此模型预报广告费用为6万元时销售额为65.5(万元).
故选:C.
6.【解答】解:设这组数据为x1,x2,…,xn,平均数为,方差为s2;
则新数据为x1﹣80,x2﹣80,…,xn﹣80,
它的平均数是=
=
=﹣80
=1.2,
∴=81.2;
方差为s′2=[++…+]
=[++…+]
=4.4=s2.
故选:A.
7.【解答】解:过点P恰存在两条直线与抛物线C有且只有一个公共点,说明P在抛物线上,
设抛物线方程为:y2=2px,代入点P(﹣1,4),可得16=﹣2p,
所求抛物线方程为:y2=﹣16x,
设抛物线方程为:x2=2py,代入点P(﹣1,4),可得1=8p,2p=.
所求抛物线方程为:x2=y,
故选:D.
8.【解答】解:根据图象的对称性知,黑色部分为圆面积的一半,设圆的半径为1,则正方形的边长为2,
则黑色部分的面积S=,
则对应概率P==,
故选:B.
9.【解答】解:模拟程序的运行,可得
n=24,S=24
执行循环体,n=16,S=40
不满足条件n=0,执行循环体,n=8,S=48
不满足条件n=0,执行循环体,n=0,S=48
满足条件n=0,可得S=47,退出循环,输出S的值为47.
故选:B.
10.【解答】解:令g(x)=x﹣lnx﹣1,则,
由g'(x)>0,得x>1,即函数g(x)在(1,+∞)上单调递增,
由g'(x)<0得0<x<1,即函数g(x)在(0,1)上单调递减,
所以当x=1时,函数g(x)有最小值,g(x)min=g(0)=0,
于是对任意的x∈(0,1)∪(1,+∞),有g(x)≥0,故排除B、D,
因函数g(x)在(0,1)上单调递减,则函数f(x)在(0,1)上递增,故排除C,
故选:A.
11.【解答】解:双曲线(a>0,b>0)的右焦点F(c,0),
过双曲线(a>0,b>0)的右焦点F且平行于其一条渐近线的直线l与另一条渐近线交于点A,
,解得A(,),|BF|=2|AB|,解得B(,),
直线l与双曲线交于点B,,e>1,解得e=.
故选:C.
12.【解答】解:f'(x)=a(1+lnx)﹣x,令f'(x)=0,
得a(1+lnx)﹣x=0,.
设,.
当g'(x)>0时,得x>1;当g'(x)<0时,得或,
所以函数g(x)在区间和上单调递减,在区间(1,+∞)上单调递增.
因为函数有且只有一个极值点,
所以直线y=a与函数的图象有一个交点,所以a<0或a=1.
当a=1时f'(x)=lnx﹣x+1≤0恒成立,所以y=f(x)无极值,所以a<0.
故选:A.
二.填空题(本题共4小题,每小题5分,共20分,把答案填在答题卷中的横线上)
13.【解答】解:∵函数y=f(x)的图象在点x=5处的切线方程是y=﹣x+8,
∴f′(5)=﹣1,f(5)=﹣5+8=3,
∴f(5)+f′(5)=3﹣1=2,
故答案为:2.
14.【解答】解:依题意,设A表示至少有1人破译出密码,
则A的对立事件表示三人都没有破译密码,
则P(A)=1﹣P()=1﹣(1﹣)××=.
故填:.
15.【解答】解:∵命题“?x∈R,x2﹣x+a<0”是假命题,
∴则命题的否定“?x∈R,x2﹣x+a≥0”为真命题,
∴△=1﹣4a≤0,解得a,
∴实数a的取值范围是[,+∞).
故答案为:[,+∞).
16.【解答】解:离心率为e==2,即c=2a,b=a,
M(﹣a,0),N(0,b),可得MN的方程为bx﹣ay+ab=0,
设P(m,n),F1(﹣c,0),F2(c,0),
可得?=(﹣c﹣m,﹣n)?(c﹣m,﹣n)=m2+n2﹣c2,
由m2+n2=()2表示原点O与P的距离的平方,
显然OP垂直于MN时,|OP|最小,
由OP:y=﹣x,即y=﹣x,联立直线x﹣y+a=0,
可得P(﹣a,a),即S1=?2c?a=a2,
当P与N重合时,可得OP的距离最大,
可得S2=?2c?b=2a2,
即有==4.
故答案为:4.
三、解答题(本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.【解答】解:(Ⅰ)由题意,(a,b,c)所有的可能为:
(1,1,1),(1,1,2),(1,1,3),(1,2,1),(1,2,2),(1,2,3),
(1,3,1),(1,3,2),(1,3,3),(2,1,1),(1,1,2),(2,1,3),
(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3),
(3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),
(3,3,1),(3,3,2),(3,3,3),共27种.
设“抽取的卡片上的数字满足a+b=c”为事件A,则事件A包括(1,1,2),(1,2,3),(2,1,3),共3种,
所以P(A)==.
因此,“抽取的卡片上的数字满足a+b=c”的概率为.
(Ⅱ)设“抽取的卡片上的数字a,b,c不完全相同”为事件B,
则事件包括(1,1,1),(2,2,2),(3,3,3),共3种.
所以P(B)=1﹣P()=1﹣=.
因此,“抽取的卡片上的数字a,b,c不完全相同”的概率为.
18.【解答】解:若A∩B=B得B?A,
若B是空集,则2﹣m>3m+1,得4m<1,得m<;
若B不是空集,则满足,得得≤m<2;
综上m<2,即p:m<2.
若只有一个实数x满足不等式x2+2mx+2m≤0,则判别式△=4m2﹣4m=0得m=0或m=1,
即q:m=0或m=1,
若命题“p或q”是假命题,则命题p和q都是假命题,即,即m≥2,
即实数m的取值范围是[2,+∞).
19.【解答】解:(1)依题意,10×(0.010+0.018+0.022)=0.45<0.5,
所以网友留言条数的中位数为30+=32;
(2)根据频率分布直方图得,网友强烈关注的频率为10×(0.020+0.005)=0.25,
所以强烈关注的人数为100×0.25=25,因为强烈关注的女行有10人,所以强烈关注的男性有15人,
所以一般关注的男性有45﹣15=30人,一般关注的女性有55﹣10=45人,
所以2×2列联表如下:
一般关注
强烈关注
合计
男
30
15
45
女
45
10
55
合计
75
25
100
(3)由(2)中的2×2列联表中数据可得:=≈3.030<3.841.
所以没有95%的把握认为网友对此事件是否为“强烈关注”与性别有关.
20.【解答】(I)解:∵椭圆E经过点A(0,﹣1),且离心率为,
∴b=1,=,
∴c=1,a=.
∴椭圆E的方程为:+y2=1.
(II)证明:由题设知,直线PQ的方程为y=k(x﹣1)+1(k≠2),
代入+y2=1,得(1+2k2)x2﹣4k(k﹣1)x+2k(k﹣2)=0.
由条件可知△>0,
设P(x1,y1),Q(x2,y2),x1x2≠0,
则x1+x2=,x1x2=,
从而直线AP,AQ的斜率之和为:
kAP+kAQ=+=+=2k+(2﹣k)=2k+(2﹣k)=2k﹣2(k﹣1)=2.
所以直线AP、AQ斜率之和为定值2.
21.【解答】解:(1)因为f(x)=x2﹣3x+2lnx,x>0,
所以f′(x)=x﹣3+=,
令f′(x)=0,解得x=1,或x=2,
当f′(x)>0时,解得0<x<1或x>2,
当f′(x)<0时,解得1<x<2,
所以其单调递增区间为(0,1),(2,+∞),单调递减区间为(1,2).
(2)若要命题成立,只需当x∈(0,2]时,f(x)max<g(x)max.由g′(x)=(x2﹣2)ex,
可知,当x∈(0,2]时,g(x)在区间(0,)上单调递减,在区间(,2]上单调递增,
g(0)=g(2)=0,故g(x)max=0,
所以只需f(x)max<0.
对函数f(x)来说,f′(x)=ax﹣(2a+1)+=.
①当≥2时,即 0<a≤,函数f(x)在区间x∈(0,2]上单调递增,
所以,f(x)max=f(2)=﹣2a﹣2+2ln2<0,
所以,a>ln2﹣1 即0<a≤,
②当0<<2时,即a>,函数f(x)在区间(0,)上单调递增,在区间(,2]上单调递减,
所以f(x)max=f()=﹣2lna﹣﹣2.
当a≥1时,显然小于0,满足题意;
当<a<1时,可令h(a)=﹣2lna﹣﹣2,
所以h′(a)=,
可知该函数在a∈(,1)时单调递减,h(a)<h()=2ln2﹣3<0,满足题意,
所以a> 满足题意.
综上所述:当a>0时,对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2)成立.
(2)另法】f(x)=ax2﹣(2a+1)x+2lnx=﹣(x﹣2lnx),
因为a>0,x∈(0,2],
所以<0
令h(x)=x﹣2lnx,则h′(x)=1﹣=,
所以h(x)在(0,2]为单调递减,h(x)≥h(2)=2﹣2ln2>0,
因此,在a>0,x∈(0,2]时,f(x)<0,
故当a>0时,对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2)成立.
【选做】请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
22.【解答】解:(1)由圆C的方程为(x+6)2+y2=25,得x2+y2+12x+11=0,
把x2+y2=ρ2,x=ρcosθ代入,得C的极坐标方程为ρ2+12ρcosθ+11=0;
(2)把θ=α代入ρ2+12ρcosθ+11=0,
得ρ2+12ρcosα+11=0,则ρA+ρB=﹣12cosα,ρA?ρB=11.
∴|AB|=|ρA﹣ρB|==.
则cos2α=,∴sin2α=,,
∴tan,即l的斜率为.
23.【解答】解:(1)当a=1时,f(x)=5﹣|x+1|﹣|x﹣2|=.
当x≤﹣1时,f(x)=2x+4≥0,解得﹣2≤x≤﹣1,
当﹣1<x<2时,f(x)=2≥0恒成立,即﹣1<x<2,
当x≥2时,f(x)=﹣2x+6≥0,解得2≤x≤3,
综上所述不等式f(x)≥0的解集为[﹣2,3],
(2)∵f(x)≤1,
∴5﹣|x+a|﹣|x﹣2|≤1,
∴|x+a|+|x﹣2|≥4,
∴|x+a|+|x﹣2|=|x+a|+|2﹣x|≥|x+a+2﹣x|=|a+2|,
∴|a+2|≥4,
解得a≤﹣6或a≥2,
故a的取值范围(﹣∞,﹣6]∪[2,+∞).
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.复数z=﹣2+i,则它的共轭复数在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.设a,b是实数,则“a+b>0”是“ab>0”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.用反证法证明命题“三角形中最多只有一个内角是钝角”时,结论的否定是( )
A.没有一个内角是钝角 B.有两个内角是钝角
C.有三个内角是钝角 D.至少有两个内角是钝角
4.某镇有A.B.C三个村,它们的精准扶贫的人口数量之比为3:4:5,现在用分层抽样的方法抽出容量为n的样本,样本中A村有15人,则样本容量为( )
A.50 B.60 C.70 D.80
5.某产品的广告费用x与销售额y的统计数据如表:
广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程=x+中的为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.67.7万元 C.65.5万元 D.72.0万元
6.一组数据中的每一个数据都减去80,得一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( )
A.81.2,4.4 B.78.8,4.4 C.81.2,84.4 D.78.8,75.6
7.已知点P(﹣1,4),过点P恰存在两条直线与抛物线C有且只有一个公共点,则抛物线C的标准方程为( )
A.x2= B.x2=4y或y2=﹣16x
C.y2=﹣16x D.x2=y或y2=﹣16x
8.如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
A. B. C. D.
9.《孙子算经》是中国古代重要的数学著作,书中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?“该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚减一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解,如图是解决这类问题的程序框图,若输入n=24,则输出的结果为( )
A.23 B.47 C.24 D.48
10.已知函数f(x)=,则y=f(x)的图象大致为( )
A. B.
C. D.
11.过双曲线(a>0,b>0)的右焦点F且平行于其一条渐近线的直线l与另一条渐近线交于点A,直线l与双曲线交于点B,且|BF|=2|AB|,则双曲线的离心率为( )
A. B. C. D.2
12.已知函数f(x)=axlnx﹣+a有且只有一个极值点,则实数a构成的集合是( )
A.{a|a<0} B.{a|a>0} C.{a|a<1} D.{a|a>1}
二.填空题(本题共4小题,每小题5分,共20分,把答案填在答题卷中的横线上)
13.函数y=f(x)在x=5处的切线方程是y=﹣x+8,则f(5)+f′(5)= .
14.甲,乙,丙三人独立破译同一份密码.已知甲乙丙各自独立破译出密码的概率分别为,且他们是否破译出密码互不影响,则至少有1人破译出密码的概率是 .
15.若命题“?x∈R,x2﹣x+a<0”是假命题,则实数a的取值范围是 .
16.已知双曲线(a>0,b>0)的离心率为2,F1,F2分别是双曲线的左、右焦点,点M(﹣a,0),N(0,b),点P为线段MN上的动点,当取得最小值和最大值时,△PF1F2的面积分别为S1,S2,则= .
三、解答题(本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(12分)一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同,随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.
(1)求“抽取的卡片上的数字满足a+b=c”的概率;
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
(注:若三个数a,b,c满足a≤b≤c,则称b为这三个数的中位数)
18.(12分)已经集合A={x|﹣1<x<7},B={x|2﹣m≤x≤3m+1},设命题p:满足A∩B=B,命题q:只有一个实数x满足不等式x2+2mx+2m≤0,若命题“p或q”是假命题,求m的取值范围.
19.(12分)2018年11月21日,意大利奢侈品牌“D&G”在广告中涉嫌辱华,中国明星纷纷站出来抵制该品牌,随后京东、天猫、唯品会等中国电商平台全线下架了该品牌商品,当天有大量网友关注此事件,某网上论坛从关注此事件跟帖中,随机抽取了100名网友进行调查统计,先分别统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到如图所示的频率分布直方图;并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计得到列联表的部分数据如表.
(1)根据如图所示的频率分布直方图,求网友留言条数的中位数;
(2)在答题卡上补全2×2列联表中数据;
(3)判断能否有95%的把握认为网友对此事件是否为“强烈关注”与性别有关?
一般关注
强烈关注
合计
男
45
女
10
55
合计
100
参考公式及数据:
P(K2≥K0)
0.05
0.025
0.010
0.005
k0
3.841
5.024
6.635
7.879
20.(12分)如图,椭圆E:+=1(a>b>0)经过点A(0,﹣1),且离心率为.
(Ⅰ)求椭圆E的方程;
(Ⅱ)经过点(1,1),且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为定值.
21.(12分)已知函数f(x)=ax2﹣(2a+1)x+2lnx(a∈R).
(1)当a=1时,求函数f(x)的单调区间;
(2)当a>0时,设g(x)=(x2﹣2x)ex,求证:对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2)成立.
【选做】请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
22.(10分)在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.
(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;
(2)直线l的极坐标方程是θ=α(ρ∈R),l与C交于A,B两点,,求l的斜率.
23.设函数f(x)=5﹣|x+a|﹣|x﹣2|.
(1)当a=1时,求不等式f(x)≥0的解集;
(2)若f(x)≤1,求a的取值范围.
2018-2019学年江西省赣州市十五县(市)高二(下)期中数学试卷(文科)
参考答案与试题解析
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.【解答】解:∵z=﹣2+i,
∴它的共轭复数=﹣2﹣i,对应的坐标为(﹣2,﹣1)位于第三象限,
故选:C.
2.【解答】解:a,b是实数,如果a=﹣1,b=2则“a+b>0”,则“ab>0”不成立.
如果a=﹣1,b=﹣2,ab>0,但是a+b>0不成立,
所以设a,b是实数,则“a+b>0”是“ab>0”的既不充分也不必要条件.
故选:D.
3.【解答】解:命题“三角形中最多只有一个内角是钝角”的结论的否定是“至少有两个内角是钝角”
故选:D.
4.【解答】解:A村所占的比例为=,
15÷=60,故样本容量n=60,
故选:B.
5.【解答】解:由表中数据得:=3.5,==42,
又回归方程=x+中的为9.4,
故=42﹣9.4×3.5=9.1,
∴=9.4x+9.1.
将x=6代入回归直线方程,得y=9.4×6+9.1=65.5(万元).
∴此模型预报广告费用为6万元时销售额为65.5(万元).
故选:C.
6.【解答】解:设这组数据为x1,x2,…,xn,平均数为,方差为s2;
则新数据为x1﹣80,x2﹣80,…,xn﹣80,
它的平均数是=
=
=﹣80
=1.2,
∴=81.2;
方差为s′2=[++…+]
=[++…+]
=4.4=s2.
故选:A.
7.【解答】解:过点P恰存在两条直线与抛物线C有且只有一个公共点,说明P在抛物线上,
设抛物线方程为:y2=2px,代入点P(﹣1,4),可得16=﹣2p,
所求抛物线方程为:y2=﹣16x,
设抛物线方程为:x2=2py,代入点P(﹣1,4),可得1=8p,2p=.
所求抛物线方程为:x2=y,
故选:D.
8.【解答】解:根据图象的对称性知,黑色部分为圆面积的一半,设圆的半径为1,则正方形的边长为2,
则黑色部分的面积S=,
则对应概率P==,
故选:B.
9.【解答】解:模拟程序的运行,可得
n=24,S=24
执行循环体,n=16,S=40
不满足条件n=0,执行循环体,n=8,S=48
不满足条件n=0,执行循环体,n=0,S=48
满足条件n=0,可得S=47,退出循环,输出S的值为47.
故选:B.
10.【解答】解:令g(x)=x﹣lnx﹣1,则,
由g'(x)>0,得x>1,即函数g(x)在(1,+∞)上单调递增,
由g'(x)<0得0<x<1,即函数g(x)在(0,1)上单调递减,
所以当x=1时,函数g(x)有最小值,g(x)min=g(0)=0,
于是对任意的x∈(0,1)∪(1,+∞),有g(x)≥0,故排除B、D,
因函数g(x)在(0,1)上单调递减,则函数f(x)在(0,1)上递增,故排除C,
故选:A.
11.【解答】解:双曲线(a>0,b>0)的右焦点F(c,0),
过双曲线(a>0,b>0)的右焦点F且平行于其一条渐近线的直线l与另一条渐近线交于点A,
,解得A(,),|BF|=2|AB|,解得B(,),
直线l与双曲线交于点B,,e>1,解得e=.
故选:C.
12.【解答】解:f'(x)=a(1+lnx)﹣x,令f'(x)=0,
得a(1+lnx)﹣x=0,.
设,.
当g'(x)>0时,得x>1;当g'(x)<0时,得或,
所以函数g(x)在区间和上单调递减,在区间(1,+∞)上单调递增.
因为函数有且只有一个极值点,
所以直线y=a与函数的图象有一个交点,所以a<0或a=1.
当a=1时f'(x)=lnx﹣x+1≤0恒成立,所以y=f(x)无极值,所以a<0.
故选:A.
二.填空题(本题共4小题,每小题5分,共20分,把答案填在答题卷中的横线上)
13.【解答】解:∵函数y=f(x)的图象在点x=5处的切线方程是y=﹣x+8,
∴f′(5)=﹣1,f(5)=﹣5+8=3,
∴f(5)+f′(5)=3﹣1=2,
故答案为:2.
14.【解答】解:依题意,设A表示至少有1人破译出密码,
则A的对立事件表示三人都没有破译密码,
则P(A)=1﹣P()=1﹣(1﹣)××=.
故填:.
15.【解答】解:∵命题“?x∈R,x2﹣x+a<0”是假命题,
∴则命题的否定“?x∈R,x2﹣x+a≥0”为真命题,
∴△=1﹣4a≤0,解得a,
∴实数a的取值范围是[,+∞).
故答案为:[,+∞).
16.【解答】解:离心率为e==2,即c=2a,b=a,
M(﹣a,0),N(0,b),可得MN的方程为bx﹣ay+ab=0,
设P(m,n),F1(﹣c,0),F2(c,0),
可得?=(﹣c﹣m,﹣n)?(c﹣m,﹣n)=m2+n2﹣c2,
由m2+n2=()2表示原点O与P的距离的平方,
显然OP垂直于MN时,|OP|最小,
由OP:y=﹣x,即y=﹣x,联立直线x﹣y+a=0,
可得P(﹣a,a),即S1=?2c?a=a2,
当P与N重合时,可得OP的距离最大,
可得S2=?2c?b=2a2,
即有==4.
故答案为:4.
三、解答题(本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.【解答】解:(Ⅰ)由题意,(a,b,c)所有的可能为:
(1,1,1),(1,1,2),(1,1,3),(1,2,1),(1,2,2),(1,2,3),
(1,3,1),(1,3,2),(1,3,3),(2,1,1),(1,1,2),(2,1,3),
(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3),
(3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),
(3,3,1),(3,3,2),(3,3,3),共27种.
设“抽取的卡片上的数字满足a+b=c”为事件A,则事件A包括(1,1,2),(1,2,3),(2,1,3),共3种,
所以P(A)==.
因此,“抽取的卡片上的数字满足a+b=c”的概率为.
(Ⅱ)设“抽取的卡片上的数字a,b,c不完全相同”为事件B,
则事件包括(1,1,1),(2,2,2),(3,3,3),共3种.
所以P(B)=1﹣P()=1﹣=.
因此,“抽取的卡片上的数字a,b,c不完全相同”的概率为.
18.【解答】解:若A∩B=B得B?A,
若B是空集,则2﹣m>3m+1,得4m<1,得m<;
若B不是空集,则满足,得得≤m<2;
综上m<2,即p:m<2.
若只有一个实数x满足不等式x2+2mx+2m≤0,则判别式△=4m2﹣4m=0得m=0或m=1,
即q:m=0或m=1,
若命题“p或q”是假命题,则命题p和q都是假命题,即,即m≥2,
即实数m的取值范围是[2,+∞).
19.【解答】解:(1)依题意,10×(0.010+0.018+0.022)=0.45<0.5,
所以网友留言条数的中位数为30+=32;
(2)根据频率分布直方图得,网友强烈关注的频率为10×(0.020+0.005)=0.25,
所以强烈关注的人数为100×0.25=25,因为强烈关注的女行有10人,所以强烈关注的男性有15人,
所以一般关注的男性有45﹣15=30人,一般关注的女性有55﹣10=45人,
所以2×2列联表如下:
一般关注
强烈关注
合计
男
30
15
45
女
45
10
55
合计
75
25
100
(3)由(2)中的2×2列联表中数据可得:=≈3.030<3.841.
所以没有95%的把握认为网友对此事件是否为“强烈关注”与性别有关.
20.【解答】(I)解:∵椭圆E经过点A(0,﹣1),且离心率为,
∴b=1,=,
∴c=1,a=.
∴椭圆E的方程为:+y2=1.
(II)证明:由题设知,直线PQ的方程为y=k(x﹣1)+1(k≠2),
代入+y2=1,得(1+2k2)x2﹣4k(k﹣1)x+2k(k﹣2)=0.
由条件可知△>0,
设P(x1,y1),Q(x2,y2),x1x2≠0,
则x1+x2=,x1x2=,
从而直线AP,AQ的斜率之和为:
kAP+kAQ=+=+=2k+(2﹣k)=2k+(2﹣k)=2k﹣2(k﹣1)=2.
所以直线AP、AQ斜率之和为定值2.
21.【解答】解:(1)因为f(x)=x2﹣3x+2lnx,x>0,
所以f′(x)=x﹣3+=,
令f′(x)=0,解得x=1,或x=2,
当f′(x)>0时,解得0<x<1或x>2,
当f′(x)<0时,解得1<x<2,
所以其单调递增区间为(0,1),(2,+∞),单调递减区间为(1,2).
(2)若要命题成立,只需当x∈(0,2]时,f(x)max<g(x)max.由g′(x)=(x2﹣2)ex,
可知,当x∈(0,2]时,g(x)在区间(0,)上单调递减,在区间(,2]上单调递增,
g(0)=g(2)=0,故g(x)max=0,
所以只需f(x)max<0.
对函数f(x)来说,f′(x)=ax﹣(2a+1)+=.
①当≥2时,即 0<a≤,函数f(x)在区间x∈(0,2]上单调递增,
所以,f(x)max=f(2)=﹣2a﹣2+2ln2<0,
所以,a>ln2﹣1 即0<a≤,
②当0<<2时,即a>,函数f(x)在区间(0,)上单调递增,在区间(,2]上单调递减,
所以f(x)max=f()=﹣2lna﹣﹣2.
当a≥1时,显然小于0,满足题意;
当<a<1时,可令h(a)=﹣2lna﹣﹣2,
所以h′(a)=,
可知该函数在a∈(,1)时单调递减,h(a)<h()=2ln2﹣3<0,满足题意,
所以a> 满足题意.
综上所述:当a>0时,对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2)成立.
(2)另法】f(x)=ax2﹣(2a+1)x+2lnx=﹣(x﹣2lnx),
因为a>0,x∈(0,2],
所以<0
令h(x)=x﹣2lnx,则h′(x)=1﹣=,
所以h(x)在(0,2]为单调递减,h(x)≥h(2)=2﹣2ln2>0,
因此,在a>0,x∈(0,2]时,f(x)<0,
故当a>0时,对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2)成立.
【选做】请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
22.【解答】解:(1)由圆C的方程为(x+6)2+y2=25,得x2+y2+12x+11=0,
把x2+y2=ρ2,x=ρcosθ代入,得C的极坐标方程为ρ2+12ρcosθ+11=0;
(2)把θ=α代入ρ2+12ρcosθ+11=0,
得ρ2+12ρcosα+11=0,则ρA+ρB=﹣12cosα,ρA?ρB=11.
∴|AB|=|ρA﹣ρB|==.
则cos2α=,∴sin2α=,,
∴tan,即l的斜率为.
23.【解答】解:(1)当a=1时,f(x)=5﹣|x+1|﹣|x﹣2|=.
当x≤﹣1时,f(x)=2x+4≥0,解得﹣2≤x≤﹣1,
当﹣1<x<2时,f(x)=2≥0恒成立,即﹣1<x<2,
当x≥2时,f(x)=﹣2x+6≥0,解得2≤x≤3,
综上所述不等式f(x)≥0的解集为[﹣2,3],
(2)∵f(x)≤1,
∴5﹣|x+a|﹣|x﹣2|≤1,
∴|x+a|+|x﹣2|≥4,
∴|x+a|+|x﹣2|=|x+a|+|2﹣x|≥|x+a+2﹣x|=|a+2|,
∴|a+2|≥4,
解得a≤﹣6或a≥2,
故a的取值范围(﹣∞,﹣6]∪[2,+∞).
同课章节目录
