9.2 多边形的内角和与外角和 (共32张PPT)
文档属性
| 名称 | 9.2 多边形的内角和与外角和 (共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 747.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 14:22:04 | ||
图片预览










文档简介
课件32张PPT。9.2多边形的内角和与外角和生活中的多边形形象观察下列图形,从多边形的一个顶点出发可以引
多少条对角线?这些对角线把多边形分成几个三
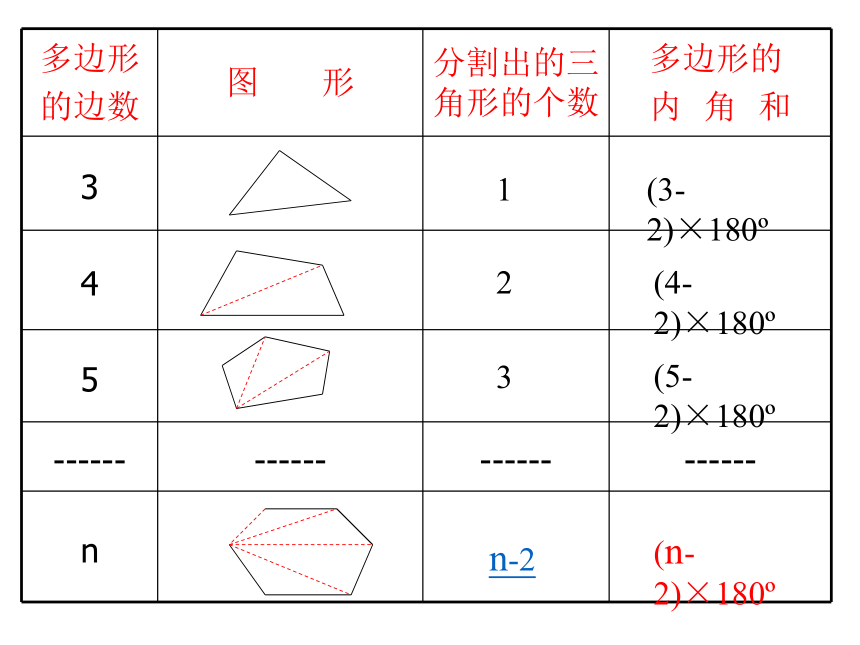
角形?你能猜想 n 边形的内角和是多少度吗?探索多边形的内角和n-2123(3-2)×180o(4-2)×180o(5-2)×180o(n-2)×180o多边形的内角和定理:
n边形的内角和等于(n-2)·180o2、你能用其他方法证明这个定理吗?1、证明多边形内角和定理的
基本思想是什么?n-2 推论:任意多边形的外角 和
等于360o 。 类比前边的做法,你能归纳出n 边形的外角和是多少吗? ∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________A1A2A3AnA4证明:180o ,(n-2) ? 180o ,∴ n 边形的外角和等于n ? 180o – (n-2) ? 180o =360o。n ? 180o,例题1已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。解:设多边形的边数为n ,
∵它的内角和等于(n-2) ? 180o ,外角
和等于360o ,
∴ (n-2)×180o=2 × 360o
解得 n=6
∴这个多边形的边数6一、填空题
十二边形的内角和是( )。
正六边形的一个内角等于( )。
一个多边形当边数增加1时,它的内角和增加( )。
一个多边形的内角和等于它的外角和,这个多边形是( )边形。
一个多边形的内角和是720o,则此多边形共有( )个内角。1800o120o180o四六二、选择题
1、从 n边形的一个顶点出发作对角线,把这个多边形分
成三角形的个数是( )。
A、n B、n-1 C、n-2 D、n-3
2、n边形所有外角的个数是( )。
A、n B、2n C、3n D、不能确定
3、下列说法中,正确的是( )。
A、一个多边形的外角的个数与边数相同;
B、一个多边形的外角的个数是边数的2倍;
C、多边形的外角和是所有外角的和;
D、多边形的外角和是内角和的一半。
4、一个多边形每个外角都是30o,这个多边形是( )。
A、十边形 B、十一边形 C、十二边形 D、十三边形CBBC120°120°120°108°108°108°1、已知一个凸多边形的每个内角都等于150度,求这个多边形的边数。开放创新题把一个长方形的桌子截去一个角,得到的多边形的内角和是几度?聪明题
已知: 如图 ∠A,∠B,∠C,
∠D,∠E,∠F,∠G,∠H八个
角的和的度数是多少度?1、n边形的内角和是(n-2)·180o,揭示了多
边形的内角和与边数的关系:当边数增
加1时,内角和增加180o。2、任意多边形的外角和都是360o,与边数
无关。多边形的内角和小结小 结在本课的学习中,同学们又一次体会到了类比、扩展、归纳、概括、从具体到抽象、化繁为简、化未知为已知等数学思想方法在数学中的应用。在平时的学习中,同学们应注意知识与知识之间的联系,灵活运用数学思想与方法,这样你才能体会到学习数学的乐趣,让数学成为你走向成功的助手。 12、如下图,某公园有一个边长为5米的正五边形水池,池内养了观赏金鱼,公园设计人员想在水池四周铺上宽为1米的漂亮大理石,供游人行走,问所需大理石至少多少平方米? 应用新知1、已知一个四边形的四个内角的度数之比是1:2:3:4,求四个内角的度数。观察下列图形,从多边形的一个顶点出发可以引多少条对角线?这些对角线把多边形分成几个三角形?你能猜想 n 边形的内角和是多少度吗?(1)(6)(5)(4)(3)(2) 多边形的内角和公式
(n-2)? 180o = n边形的内角和
什么时候可以顺向应用?什么时候可以逆向应用?已知边数求多边形的内角和 — 直接应用内角和公式。已知多边形的内角和求边数 — 逆向应用多边形内角和公式解关于n的方程。六角螺母的一个面是六边形的,这个六边形的六个内角相等,求每一个内角的度数。
一个多边形的内角和等于1080 o ,求它的边数。三、解答题课堂小结:1、通过与三角形的类比,得到四边形的有关概念
2、四边形的内角和等于360度
3、多边形的外角和都等于360度
4、推导出了求多边形内角和的公式谢谢 再见
多少条对角线?这些对角线把多边形分成几个三
角形?你能猜想 n 边形的内角和是多少度吗?探索多边形的内角和n-2123(3-2)×180o(4-2)×180o(5-2)×180o(n-2)×180o多边形的内角和定理:
n边形的内角和等于(n-2)·180o2、你能用其他方法证明这个定理吗?1、证明多边形内角和定理的
基本思想是什么?n-2 推论:任意多边形的外角 和
等于360o 。 类比前边的做法,你能归纳出n 边形的外角和是多少吗? ∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________A1A2A3AnA4证明:180o ,(n-2) ? 180o ,∴ n 边形的外角和等于n ? 180o – (n-2) ? 180o =360o。n ? 180o,例题1已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。解:设多边形的边数为n ,
∵它的内角和等于(n-2) ? 180o ,外角
和等于360o ,
∴ (n-2)×180o=2 × 360o
解得 n=6
∴这个多边形的边数6一、填空题
十二边形的内角和是( )。
正六边形的一个内角等于( )。
一个多边形当边数增加1时,它的内角和增加( )。
一个多边形的内角和等于它的外角和,这个多边形是( )边形。
一个多边形的内角和是720o,则此多边形共有( )个内角。1800o120o180o四六二、选择题
1、从 n边形的一个顶点出发作对角线,把这个多边形分
成三角形的个数是( )。
A、n B、n-1 C、n-2 D、n-3
2、n边形所有外角的个数是( )。
A、n B、2n C、3n D、不能确定
3、下列说法中,正确的是( )。
A、一个多边形的外角的个数与边数相同;
B、一个多边形的外角的个数是边数的2倍;
C、多边形的外角和是所有外角的和;
D、多边形的外角和是内角和的一半。
4、一个多边形每个外角都是30o,这个多边形是( )。
A、十边形 B、十一边形 C、十二边形 D、十三边形CBBC120°120°120°108°108°108°1、已知一个凸多边形的每个内角都等于150度,求这个多边形的边数。开放创新题把一个长方形的桌子截去一个角,得到的多边形的内角和是几度?聪明题
已知: 如图 ∠A,∠B,∠C,
∠D,∠E,∠F,∠G,∠H八个
角的和的度数是多少度?1、n边形的内角和是(n-2)·180o,揭示了多
边形的内角和与边数的关系:当边数增
加1时,内角和增加180o。2、任意多边形的外角和都是360o,与边数
无关。多边形的内角和小结小 结在本课的学习中,同学们又一次体会到了类比、扩展、归纳、概括、从具体到抽象、化繁为简、化未知为已知等数学思想方法在数学中的应用。在平时的学习中,同学们应注意知识与知识之间的联系,灵活运用数学思想与方法,这样你才能体会到学习数学的乐趣,让数学成为你走向成功的助手。 12、如下图,某公园有一个边长为5米的正五边形水池,池内养了观赏金鱼,公园设计人员想在水池四周铺上宽为1米的漂亮大理石,供游人行走,问所需大理石至少多少平方米? 应用新知1、已知一个四边形的四个内角的度数之比是1:2:3:4,求四个内角的度数。观察下列图形,从多边形的一个顶点出发可以引多少条对角线?这些对角线把多边形分成几个三角形?你能猜想 n 边形的内角和是多少度吗?(1)(6)(5)(4)(3)(2) 多边形的内角和公式
(n-2)? 180o = n边形的内角和
什么时候可以顺向应用?什么时候可以逆向应用?已知边数求多边形的内角和 — 直接应用内角和公式。已知多边形的内角和求边数 — 逆向应用多边形内角和公式解关于n的方程。六角螺母的一个面是六边形的,这个六边形的六个内角相等,求每一个内角的度数。
一个多边形的内角和等于1080 o ,求它的边数。三、解答题课堂小结:1、通过与三角形的类比,得到四边形的有关概念
2、四边形的内角和等于360度
3、多边形的外角和都等于360度
4、推导出了求多边形内角和的公式谢谢 再见
