《统计案例》章节小结归纳整合
图片预览










文档简介
会宁一中
《统计案例》小结
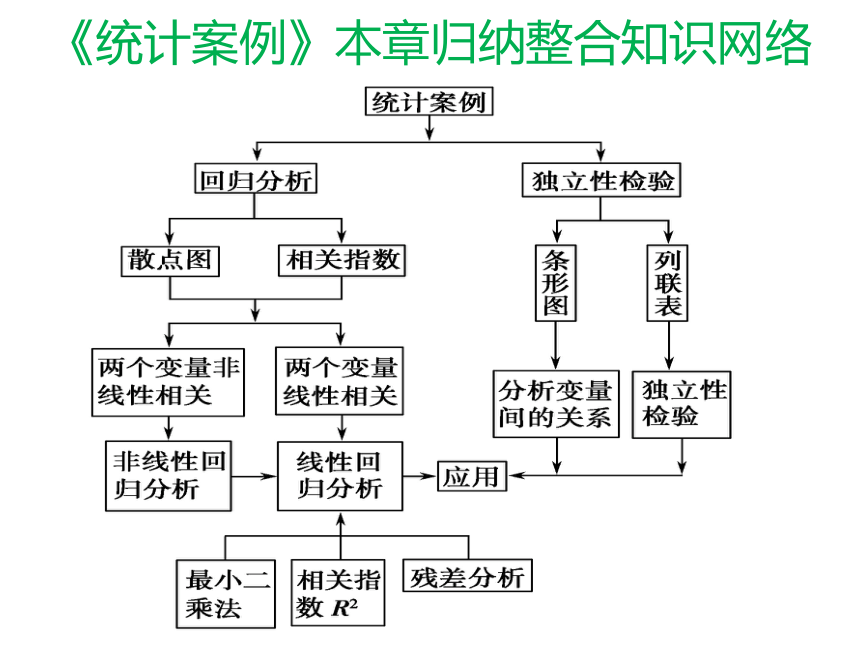
《统计案例》本章归纳整合知识网络
例题讲解
1、求回归直线方程的方法与技巧
例1(安徽卷)某地最近十年粮食需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量与年份之间的回归直线方程 ;(2)利用(1)中所求出的直线方程预测该地2012年的粮食需求量.
解:(1)设年份x,需求量y( 万吨):
年份 2002 2004 2006 2008 2010
需求量(万吨) 236 246 257 276 286
-4 -2 0 2 4
-21 -11 0 19 29
代入所求回归直线方程中:
-4 -2 0 2 4
-21 -11 0 19 29
练习1 .在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
(1)作出散点图,你能从散点图中发现投入量x与产量y的一般规律吗?(2)求回归直线方程.(3)预测当投入量x=14时,产量y是多少?
0 1 2 3
解:(1)作出散点图如右图所示:
投入量x与产量y是线性正相关,
随着投入量x产量y逐渐增加。
x 0 1 2 3
y 1 2 4 5
(2)从图中可以看出,各点散布在一条直线附近,即它们线性相关.
(3)
预测当产量x=14时,所需的投入量x是20.5.
2、相关指数的计算
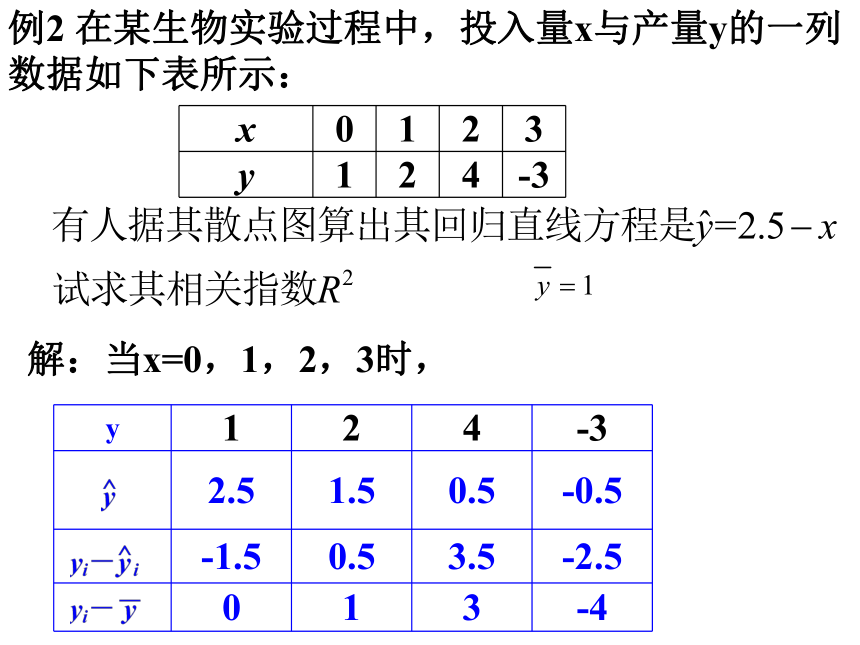
例2 在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
解:当x=0,1,2,3时,
x 0 1 2 3
y 1 2 4 -3
y 1 2 4 -3
2.5 1.5 0.5 -0.5
-1.5 0.5 3.5 -2.5
0 1 3 -4
解:当x=0,1,2,3时,
y 1 2 4 -3
2.5 1.5 0.5 -0.5
-1.5 0.5 3.5 -2.5
0 1 3 -4
0 1 2 3
相关指数越大,越接近于1,,模拟的拟合效果越好;相关指数越小,拟合的效果越差!
3、回归方程的模型
1.直线方程模型;
2.指数函数模型;
3.二次函数模型;
4.反比例函数模型;
5.对数函数模型.
1.直线方程模型.
2.指数函数模型.
3.二次函数模型.
4.反比例函数模型.
5.对数函数模型.
例3 在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
(1)画出散点图;(2)试建立y与x之间的回归方程.
解:(1)作出散点图如右图所示:
x 0 1 2 3
y 2 4 16 32
x 0 1 2 3
z 1 2 4 5
(2)
y与x之间的回归方程是:
4.独立性检验的基本思想
K方统计量
0.1%把握为为A与B无关
1%把握认为A与B无关
99.9%把握认为A与B有关
99%把握认
为A与B有关
90%把握认
为A与B有关
10%把握认为A与B无关
没有充分的依据显示A与B有关,但也不能显示A与B无关
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
例4.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出500件,量其内径尺寸,结果如下表:
(1)利用等高条形图比较两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
甲厂 [29.86,29.90) [29.90,29.94) [29.94,29.98) [29.98,30.02) [30.02,30.06) [30.06,30.10) [30.10,30.14)
频数 12 63 86 182 92 61 4
乙厂 [29.86,29.90) [29.90,29.94) [29.94,29.98) [29.98,30.02) [30.02,30.06) [30.06,30.10) [30.10,30.14)
频数 29 71 85 159 76 62 18
P(K2≥k0) 0.05 0.01
k0 3.841 6.635
0.9
1
0
0.5
0.4
0.3
0.2
0.1
0.6
0.7
0.8
优质品
非优质品
乙厂
甲厂
(2)
(8分)
甲厂 乙厂 总计
优质品 360 320 680
非优质品 140 180 320
总计 500 500 1 000
课堂训练
B
2.为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.能否在犯错误的概率不超过0.1的前提下,认为“学生选报文、理科与对外语的兴趣有关”?
解:根据题目所给的数据得到如下列联表:
理科 文科 总计
有兴趣 138 73 211
无兴趣 98 52 150
总计 236 125 361
138 73 211
98 52 150
236 125 361
因为1.871×10-4<2.706,所以,在犯错误的概率不超过0.1的前提下,不能认为“学生选报文、理科与对外语的兴趣有关”.
理科 文科 总计
有兴趣 138 73 211
无兴趣 98 52 150
总计 236 125 361
3.观察下列各图,其中两个分类变量x,y之间关系最强的是 ( )
选D.D图中两个深色条的高相差最明显,说明两个分类变量之间关系最强.
D
4.分类变量X和Y的列联表如下,则下列说法中正确的是( )
A. 越小,说明X与Y的相关性越弱
B. 越大,说明X与Y的相关性越强
C. 越大,说明X与Y的相关性越强
D. 越接近于0,说明X与Y的相关性越强
解析】选C.因为k当(ad-bc)2越大时,k越大,说明X与Y关系越强
.
C
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
5.下列命题中:①回归直线除了经过样本点的中心,还至少经过一个样本点;②将一组数据中的每个数都减去同一个数后,平均值有变化,方差没有变化;③对分类变量X与Y,它们的随机变
量的观测值
越小,“X与Y有关系”的把握程度越
模型拟合的效果越好.其中正确命题的序号为
_________________.
大;④比较两个模型的拟合效果时,如果模型残
差平方和越小,则相应的相关指数 越大,该
②④
6.某种商品的广告费支出x与销售额y(单位:万元)之间有如下对应数据,根据表中提供的全部数据,用最小二乘法得出 与x的线性回归方程为
,则表中的m的值为( )
A.45 B.50 C.55 D.60
本中心点(5,50),
则m=60,故选D.
解析 因为线性回归方程为 恒过样
x 2 4 5 6 8
y 30 40 m 50 70
课后作业
见讲义1,2题
1.下面是一个2×2列联表,则表中a,b处的值分别为( )
A.94,96 B.52,50 C.52,60 D.54,52
选C.由题意知a+21=73,a+8=b,解得a=52,b=60
.
y1 y2 总计
x1 a 21 73
x2 8 25 33
总计 b 46 106
2. 在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
(1)画出散点图;(2)试建立y与x之间的回归方程.
解:(1)作出散点图如右图所示, 其曲线模型是
x 0 1 2 3
y 1 0.5 0.25 0.2
x 0 1 2 3
z 1 2 4 5
(2)
y与x之间的回归方程是:
《统计案例》小结
《统计案例》本章归纳整合知识网络
例题讲解
1、求回归直线方程的方法与技巧
例1(安徽卷)某地最近十年粮食需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量与年份之间的回归直线方程 ;(2)利用(1)中所求出的直线方程预测该地2012年的粮食需求量.
解:(1)设年份x,需求量y( 万吨):
年份 2002 2004 2006 2008 2010
需求量(万吨) 236 246 257 276 286
-4 -2 0 2 4
-21 -11 0 19 29
代入所求回归直线方程中:
-4 -2 0 2 4
-21 -11 0 19 29
练习1 .在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
(1)作出散点图,你能从散点图中发现投入量x与产量y的一般规律吗?(2)求回归直线方程.(3)预测当投入量x=14时,产量y是多少?
0 1 2 3
解:(1)作出散点图如右图所示:
投入量x与产量y是线性正相关,
随着投入量x产量y逐渐增加。
x 0 1 2 3
y 1 2 4 5
(2)从图中可以看出,各点散布在一条直线附近,即它们线性相关.
(3)
预测当产量x=14时,所需的投入量x是20.5.
2、相关指数的计算
例2 在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
解:当x=0,1,2,3时,
x 0 1 2 3
y 1 2 4 -3
y 1 2 4 -3
2.5 1.5 0.5 -0.5
-1.5 0.5 3.5 -2.5
0 1 3 -4
解:当x=0,1,2,3时,
y 1 2 4 -3
2.5 1.5 0.5 -0.5
-1.5 0.5 3.5 -2.5
0 1 3 -4
0 1 2 3
相关指数越大,越接近于1,,模拟的拟合效果越好;相关指数越小,拟合的效果越差!
3、回归方程的模型
1.直线方程模型;
2.指数函数模型;
3.二次函数模型;
4.反比例函数模型;
5.对数函数模型.
1.直线方程模型.
2.指数函数模型.
3.二次函数模型.
4.反比例函数模型.
5.对数函数模型.
例3 在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
(1)画出散点图;(2)试建立y与x之间的回归方程.
解:(1)作出散点图如右图所示:
x 0 1 2 3
y 2 4 16 32
x 0 1 2 3
z 1 2 4 5
(2)
y与x之间的回归方程是:
4.独立性检验的基本思想
K方统计量
0.1%把握为为A与B无关
1%把握认为A与B无关
99.9%把握认为A与B有关
99%把握认
为A与B有关
90%把握认
为A与B有关
10%把握认为A与B无关
没有充分的依据显示A与B有关,但也不能显示A与B无关
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
例4.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出500件,量其内径尺寸,结果如下表:
(1)利用等高条形图比较两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
甲厂 [29.86,29.90) [29.90,29.94) [29.94,29.98) [29.98,30.02) [30.02,30.06) [30.06,30.10) [30.10,30.14)
频数 12 63 86 182 92 61 4
乙厂 [29.86,29.90) [29.90,29.94) [29.94,29.98) [29.98,30.02) [30.02,30.06) [30.06,30.10) [30.10,30.14)
频数 29 71 85 159 76 62 18
P(K2≥k0) 0.05 0.01
k0 3.841 6.635
0.9
1
0
0.5
0.4
0.3
0.2
0.1
0.6
0.7
0.8
优质品
非优质品
乙厂
甲厂
(2)
(8分)
甲厂 乙厂 总计
优质品 360 320 680
非优质品 140 180 320
总计 500 500 1 000
课堂训练
B
2.为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.能否在犯错误的概率不超过0.1的前提下,认为“学生选报文、理科与对外语的兴趣有关”?
解:根据题目所给的数据得到如下列联表:
理科 文科 总计
有兴趣 138 73 211
无兴趣 98 52 150
总计 236 125 361
138 73 211
98 52 150
236 125 361
因为1.871×10-4<2.706,所以,在犯错误的概率不超过0.1的前提下,不能认为“学生选报文、理科与对外语的兴趣有关”.
理科 文科 总计
有兴趣 138 73 211
无兴趣 98 52 150
总计 236 125 361
3.观察下列各图,其中两个分类变量x,y之间关系最强的是 ( )
选D.D图中两个深色条的高相差最明显,说明两个分类变量之间关系最强.
D
4.分类变量X和Y的列联表如下,则下列说法中正确的是( )
A. 越小,说明X与Y的相关性越弱
B. 越大,说明X与Y的相关性越强
C. 越大,说明X与Y的相关性越强
D. 越接近于0,说明X与Y的相关性越强
解析】选C.因为k当(ad-bc)2越大时,k越大,说明X与Y关系越强
.
C
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
5.下列命题中:①回归直线除了经过样本点的中心,还至少经过一个样本点;②将一组数据中的每个数都减去同一个数后,平均值有变化,方差没有变化;③对分类变量X与Y,它们的随机变
量的观测值
越小,“X与Y有关系”的把握程度越
模型拟合的效果越好.其中正确命题的序号为
_________________.
大;④比较两个模型的拟合效果时,如果模型残
差平方和越小,则相应的相关指数 越大,该
②④
6.某种商品的广告费支出x与销售额y(单位:万元)之间有如下对应数据,根据表中提供的全部数据,用最小二乘法得出 与x的线性回归方程为
,则表中的m的值为( )
A.45 B.50 C.55 D.60
本中心点(5,50),
则m=60,故选D.
解析 因为线性回归方程为 恒过样
x 2 4 5 6 8
y 30 40 m 50 70
课后作业
见讲义1,2题
1.下面是一个2×2列联表,则表中a,b处的值分别为( )
A.94,96 B.52,50 C.52,60 D.54,52
选C.由题意知a+21=73,a+8=b,解得a=52,b=60
.
y1 y2 总计
x1 a 21 73
x2 8 25 33
总计 b 46 106
2. 在某生物实验过程中,投入量x与产量y的一列数据如下表所示:
(1)画出散点图;(2)试建立y与x之间的回归方程.
解:(1)作出散点图如右图所示, 其曲线模型是
x 0 1 2 3
y 1 0.5 0.25 0.2
x 0 1 2 3
z 1 2 4 5
(2)
y与x之间的回归方程是:
