16.1.1 分式 课件(35张PPT)
文档属性
| 名称 | 16.1.1 分式 课件(35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 928.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 00:00:00 | ||
图片预览









文档简介
课件35张PPT。第16章 分式
16.1 分式及其基本性质
1.分式
请你来填一填:
(1)面积为2平方米的长方形一边长3米,则它的另一
边长为_______米;
(2)面积为S平方米的长方形一边长a米,则它的另一
边长为_______米;
(3)已知正方形的周长是 cm,则一边的长是 cm,
面积是_______cm2;
(4)一箱苹果售价P元,总重m千克,箱重n千克,则每
千克苹果的售价是______元.两个整数相除,不能整除时结果可用分数表示,当两个整式不能整除时,它们的商怎么表示呢?新课导入分式的概念问:在上面所列出的代数式中,哪些是整式?哪些不是?它们之间有什么区别?答:整式有①③④ ,整式的特点是分母不含字母;②⑤,这两个代数式不同于前面学过的整式,是两个分母含有字母的代数式.在实际应用中,某些数量关系只用整式来表示是不够的,因此,我们需要学习新的式子,以满足解决实际问题的需求.一、我们在小学学习分数时,把两个整数相
除,如2÷3,可表示为 的形式,并把 叫做
分数。类似地,如果用A、B表示两个整式,
A÷B可表示成 的形式,若B中含有字母,
且B≠0,式子 叫做分式。 分式的概念:即形如 (A、B是整式,
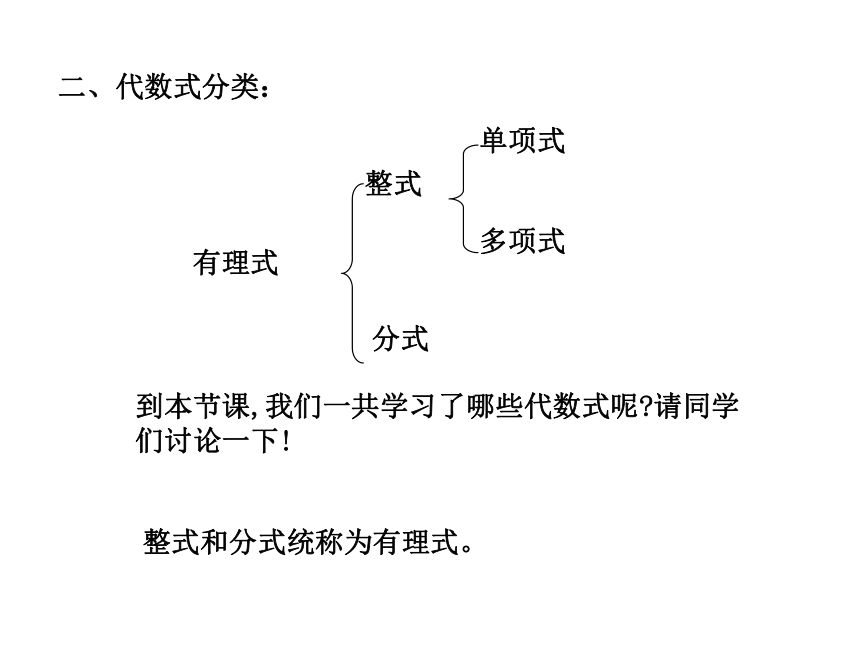
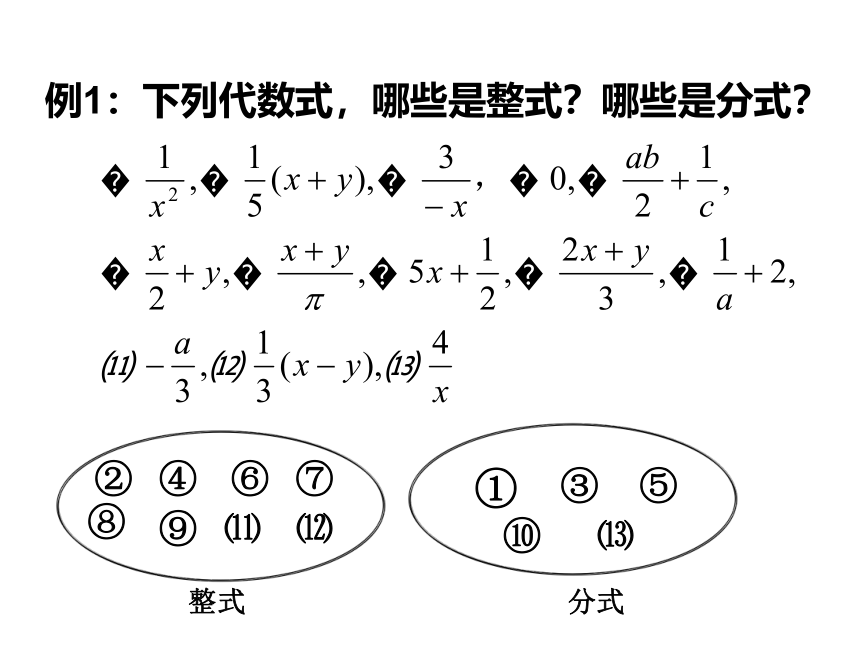
且B中含有字母,B≠0)的式子叫分式。推进新课分式整式单项式多项式二、代数式分类:有理式到本节课,我们一共学习了哪些代数式呢?请同学们讨论一下!整式和分式统称为有理式。例1:下列代数式,哪些是整式?哪些是分式?①②③④⑤⑥⑦⑧⑨⑩⑾⑿⒀整式分式1、判断一个有理式是不是分式,
关键看是否符合下式:
2、整式包括单项式和多项式,单个字母或数字是单项式。整式与分式的识别知识要点从分式的意义中,应注意以下三点:(2)分式的分子可以含有字母,也可以不含有字母,但分母必须含有字母 (3)分式分母的值不能为零.如果分母的值为零,那么分式就无意义.(1)分式是两个整式相除的商,分数线可以理 解为除号,并含有括号的作用;例2 (1)当x为何值时,分式 有意义?
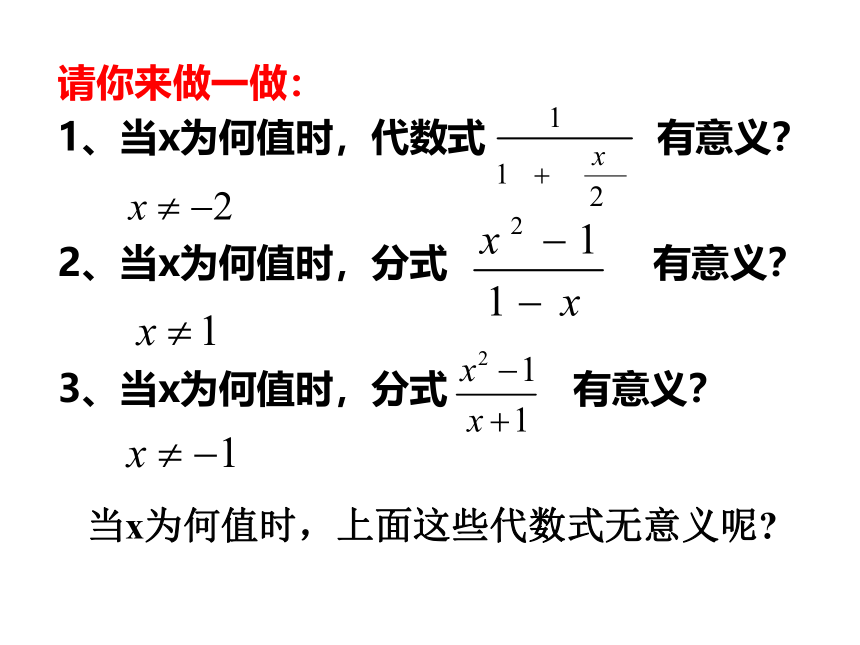
(2)当x为何值时,分式 有意义?分析:要使分式有意义,必须且只须分母不等于零。例3 当x为何值时,分式 无意义? 请你来做一做:2、当x为何值时,分式 有意义?3、当x为何值时,分式 有意义?当x为何值时,上面这些代数式无意义呢?例4.当y取什么值时,分式 的值是零?
解:①使得分式的值为0,则2y+1=0
∴y =
②使得分式有意义,则4y-1≠0
∴y ≠
∴当y = 时,此分式的值是零。友情提示:分式的定义
分式的意义
分式的值为0讨论:若分式
的值为0,则x的值是多少?解: ① |x|-3 = 0
|x| = 3
∴x =±3
②把x= - 3 代入,分母为0,分式没有意义
把x=3代入,分母等于12
∴当x = 3时,此分式值为0。随堂演练自主练习:
1、当x为何值时,代数式 有意义?
2、当x为何值时,分式 无意义?
3、当x为何值时,分式 的值为零?
4、x为何整数时,分式 的值为整数? 通过这节课的学习活动,你有什么收获?课堂小结16.1 分式及其基本性质 2.分式的基本性质 当x取什么值时,下列分式有意义?复习回顾分式 (a≠0)与 相等吗?
分式 (n≠0)与 相等吗?
说说你的理由。 新课导入 分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.分式的基本性质: 分数的基本性质:分数的分子分母都乘以(或除以)同一个不等于零的数,分数的值不变.推进新课下列各组分式,能否由左边变形为右边?
与反思:运用分式的基本性质应注意什么?(1)“都”(2)“同一个”(3)“不为0”
(2) 与
(3) 与(4) 与判 断反思:为什么(1)中有附加条件y≠0,
而(2)中没有附加条件x≠0?
例.(1)中若y为0,则 无意义,那么左右两边便不相等,所以必须加上附加条件y≠0 ;(2)中分式本身有意义便是已指出b与x都不为0,故无须再加上附加条件.填空,使等式成立.
⑴ (其中 x+y ≠0 )
⑵
想一想反思:你是怎么想的?约分: 把分式分子、分母的公因式约去,这种变形叫分式的约分.问:分式约分的依据是什么?答:分式的基本性质例1(1)(2) 约去系数的最大公约数,和分子分母相同字母的最低次幂 先把分子、分母分别分解因式,然后约去公因式.约分:分子与分母没有公因式的分式称为最简分式.(1)求分式的最简公分母。 分析:对于三个分式的分母中的系数2,4,6,取其最小公倍数12;对于三个分式的分母的字母,字母x为底的幂的因式,取其最高次幂x3,字母y为底的幂的因式,取其最高次幂y4,再取字母z.所以三个分式的公分母为12x3y4z.议一议(2)求分式与的最简公分母.=-2x(x-2)把这两个分式的分母中所有的因式都取到,其中,系数取正数,取它们的积,即就是这两个分式的最简公分母.2x(x+2) (x-2)4x-2x2 = 2x(2 -x)x2-4 = (x+2)(x -2) 的最简公分母是________________.(3)分式a2-4a +4= (a -2)24a2-8a +4= 4(a -1)23a - 6= 3(a -2)12(a -2)2 (a -1)2通分:通分的关键是确定几个分式的公分母,通常取各分母所有因式的最高次幂的积作为公分母. 例2(3),∵ x2-y2=____________,x2 +xy=__________,∴ 与 的最简公分母为____________,因此=________________,=________________,(x+y)(x-y)x(x+y)x(x+y)(x-y)先把分母分解因式一、分式的基本性质 分式的分子与分母都乘以(或除以)同一个 不为零的整式,分式的值不变.课堂小结二、分式的约分和最简分式分式的约分:把一个分式的分子和分母的公因式约去,这种变形称为分式的约分。(化简分式时,通常要使结果成为最简分式或者整式)最简分式:分子和分母没有公因式的分式叫最简分式。1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业 青春是有限的,智慧是无穷的,趁短的青春,去学习无穷的智慧。——高尔基
(1)面积为2平方米的长方形一边长3米,则它的另一
边长为_______米;
(2)面积为S平方米的长方形一边长a米,则它的另一
边长为_______米;
(3)已知正方形的周长是 cm,则一边的长是 cm,
面积是_______cm2;
(4)一箱苹果售价P元,总重m千克,箱重n千克,则每
千克苹果的售价是______元.两个整数相除,不能整除时结果可用分数表示,当两个整式不能整除时,它们的商怎么表示呢?新课导入分式的概念问:在上面所列出的代数式中,哪些是整式?哪些不是?它们之间有什么区别?答:整式有①③④ ,整式的特点是分母不含字母;②⑤,这两个代数式不同于前面学过的整式,是两个分母含有字母的代数式.在实际应用中,某些数量关系只用整式来表示是不够的,因此,我们需要学习新的式子,以满足解决实际问题的需求.一、我们在小学学习分数时,把两个整数相
除,如2÷3,可表示为 的形式,并把 叫做
分数。类似地,如果用A、B表示两个整式,
A÷B可表示成 的形式,若B中含有字母,
且B≠0,式子 叫做分式。 分式的概念:即形如 (A、B是整式,
且B中含有字母,B≠0)的式子叫分式。推进新课分式整式单项式多项式二、代数式分类:有理式到本节课,我们一共学习了哪些代数式呢?请同学们讨论一下!整式和分式统称为有理式。例1:下列代数式,哪些是整式?哪些是分式?①②③④⑤⑥⑦⑧⑨⑩⑾⑿⒀整式分式1、判断一个有理式是不是分式,
关键看是否符合下式:
2、整式包括单项式和多项式,单个字母或数字是单项式。整式与分式的识别知识要点从分式的意义中,应注意以下三点:(2)分式的分子可以含有字母,也可以不含有字母,但分母必须含有字母 (3)分式分母的值不能为零.如果分母的值为零,那么分式就无意义.(1)分式是两个整式相除的商,分数线可以理 解为除号,并含有括号的作用;例2 (1)当x为何值时,分式 有意义?
(2)当x为何值时,分式 有意义?分析:要使分式有意义,必须且只须分母不等于零。例3 当x为何值时,分式 无意义? 请你来做一做:2、当x为何值时,分式 有意义?3、当x为何值时,分式 有意义?当x为何值时,上面这些代数式无意义呢?例4.当y取什么值时,分式 的值是零?
解:①使得分式的值为0,则2y+1=0
∴y =
②使得分式有意义,则4y-1≠0
∴y ≠
∴当y = 时,此分式的值是零。友情提示:分式的定义
分式的意义
分式的值为0讨论:若分式
的值为0,则x的值是多少?解: ① |x|-3 = 0
|x| = 3
∴x =±3
②把x= - 3 代入,分母为0,分式没有意义
把x=3代入,分母等于12
∴当x = 3时,此分式值为0。随堂演练自主练习:
1、当x为何值时,代数式 有意义?
2、当x为何值时,分式 无意义?
3、当x为何值时,分式 的值为零?
4、x为何整数时,分式 的值为整数? 通过这节课的学习活动,你有什么收获?课堂小结16.1 分式及其基本性质 2.分式的基本性质 当x取什么值时,下列分式有意义?复习回顾分式 (a≠0)与 相等吗?
分式 (n≠0)与 相等吗?
说说你的理由。 新课导入 分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.分式的基本性质: 分数的基本性质:分数的分子分母都乘以(或除以)同一个不等于零的数,分数的值不变.推进新课下列各组分式,能否由左边变形为右边?
与反思:运用分式的基本性质应注意什么?(1)“都”(2)“同一个”(3)“不为0”
(2) 与
(3) 与(4) 与判 断反思:为什么(1)中有附加条件y≠0,
而(2)中没有附加条件x≠0?
例.(1)中若y为0,则 无意义,那么左右两边便不相等,所以必须加上附加条件y≠0 ;(2)中分式本身有意义便是已指出b与x都不为0,故无须再加上附加条件.填空,使等式成立.
⑴ (其中 x+y ≠0 )
⑵
想一想反思:你是怎么想的?约分: 把分式分子、分母的公因式约去,这种变形叫分式的约分.问:分式约分的依据是什么?答:分式的基本性质例1(1)(2) 约去系数的最大公约数,和分子分母相同字母的最低次幂 先把分子、分母分别分解因式,然后约去公因式.约分:分子与分母没有公因式的分式称为最简分式.(1)求分式的最简公分母。 分析:对于三个分式的分母中的系数2,4,6,取其最小公倍数12;对于三个分式的分母的字母,字母x为底的幂的因式,取其最高次幂x3,字母y为底的幂的因式,取其最高次幂y4,再取字母z.所以三个分式的公分母为12x3y4z.议一议(2)求分式与的最简公分母.=-2x(x-2)把这两个分式的分母中所有的因式都取到,其中,系数取正数,取它们的积,即就是这两个分式的最简公分母.2x(x+2) (x-2)4x-2x2 = 2x(2 -x)x2-4 = (x+2)(x -2) 的最简公分母是________________.(3)分式a2-4a +4= (a -2)24a2-8a +4= 4(a -1)23a - 6= 3(a -2)12(a -2)2 (a -1)2通分:通分的关键是确定几个分式的公分母,通常取各分母所有因式的最高次幂的积作为公分母. 例2(3),∵ x2-y2=____________,x2 +xy=__________,∴ 与 的最简公分母为____________,因此=________________,=________________,(x+y)(x-y)x(x+y)x(x+y)(x-y)先把分母分解因式一、分式的基本性质 分式的分子与分母都乘以(或除以)同一个 不为零的整式,分式的值不变.课堂小结二、分式的约分和最简分式分式的约分:把一个分式的分子和分母的公因式约去,这种变形称为分式的约分。(化简分式时,通常要使结果成为最简分式或者整式)最简分式:分子和分母没有公因式的分式叫最简分式。1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业 青春是有限的,智慧是无穷的,趁短的青春,去学习无穷的智慧。——高尔基
