9.2.1多边形的内角和学案(表格式,无答案)
文档属性
| 名称 | 9.2.1多边形的内角和学案(表格式,无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 12.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-30 00:00:00 | ||
图片预览

文档简介
9.2.1多边形的内角和
班级:______姓名:___________
学习目标:
1、了解多边形的有关概念,理解并掌握多边形的内角和
2、会推导多边形的内角和公式且能灵活运用
重点:多边形内角和定理的探索和应用
难点:多边形的内角和定理的推导
一、复习导入,明确目标(3分钟)
1、什么是三角形?
2、什么是三角形的内角?
3、三角形的内角和是多少?
二、任务驱动,分步探究 探究点一:多边形的有关概念
预习课本83-84页,思考问题
你能仿照三角形的定义说出四边形、五边形的概念吗?
n边形的概念呢
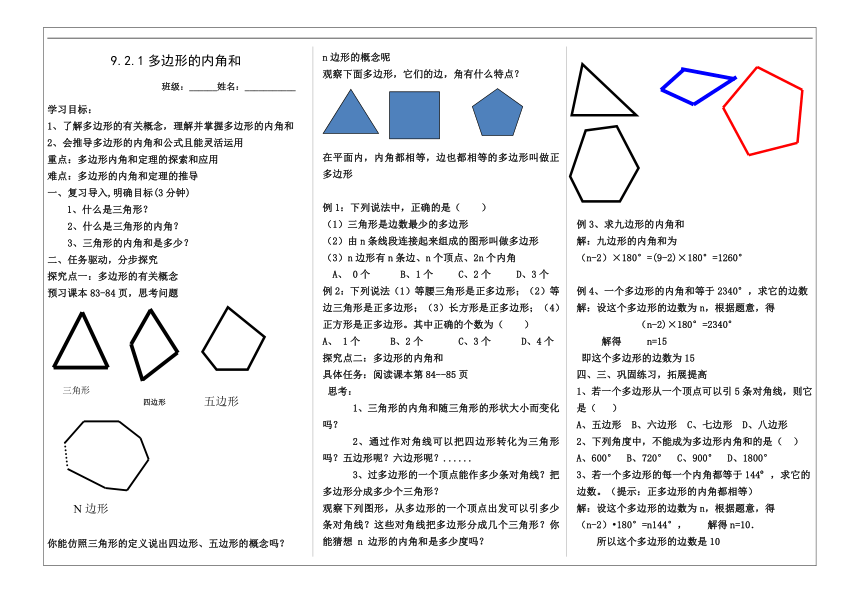
观察下面多边形,它们的边,角有什么特点?
在平面内,内角都相等,边也都相等的多边形叫做正多边形
例1:下列说法中,正确的是( )
(1)三角形是边数最少的多边形
(2)由n条线段连接起来组成的图形叫做多边形
(3)n边形有n条边、n个顶点、2n个内角
A、 0个 B、1个 C、2个 D、3个
例2:下列说法(1)等腰三角形是正多边形;(2)等边三角形是正多边形;(3)长方形是正多边形;(4)正方形是正多边形。其中正确的个数为( )
A、 1个 B、2个 C、3个 D、4个
探究点二:多边形的内角和
具体任务:阅读课本第84--85页
思考:
1、三角形的内角和随三角形的形状大小而变化吗?
2、通过作对角线可以把四边形转化为三角形吗?五边形呢?六边形呢?......
3、过多边形的一个顶点能作多少条对角线?把多边形分成多少个三角形?
观察下列图形,从多边形的一个顶点出发可以引多少条对角线?这些对角线把多边形分成几个三角形?你能猜想 n 边形的内角和是多少度吗?
例3、求九边形的内角和
解:九边形的内角和为
(n-2)×180°=(9-2)×180°=1260°
例4、一个多边形的内角和等于2340°,求它的边数
解:设这个多边形的边数为n,根据题意,得
(n-2)×180°=2340°
解得 n=15
即这个多边形的边数为15
三、巩固练习,拓展提高
1、若一个多边形从一个顶点可以引5条对角线,则它
是( )
A、五边形 B、六边形 C、七边形 D、八边形
2、下列角度中,不能成为多边形内角和的是( )
A、600° B、720° C、900° D、1800°
3、若一个多边形的每一个内角都等于144o ,求它的
边数。(提示:正多边形的内角都相等)
解:设这个多边形的边数为n,根据题意,得
(n-2)?180°=n144°, 解得n=10.
所以这个多边形的边数是10
课堂小结,回扣目标
三角形、四边形都属于多边形,所以四 边形的定义、边、顶点、内角、内角和等概念可类比地扩展到多边形。
、n边形的内角和为(n-2) ×180°(n≥3)
中考链接
(广东中考)一个多边形的内角和是900°,这个多边形的边数是( )
A、10 B、9 C、8 D、7
五、达标检测(10分钟,共10分)
姓名 班级 小组
八边形的内角和是( )
A、1440° B、1260° C、1080° D、900°
2、四边形的内角的度数之比为2∶3∶5∶8, 则各个角的度数分别是
3、一个多边形的内角和比四边形内角和的3倍多180°,则这个多边形的边数是
4、已知多边形的每一内角为150°,求这个多边形的边数.
学(教)后反思:
我的收获是: ________________________________________________
我的问题是: _____________________________________________
班级:______姓名:___________
学习目标:
1、了解多边形的有关概念,理解并掌握多边形的内角和
2、会推导多边形的内角和公式且能灵活运用
重点:多边形内角和定理的探索和应用
难点:多边形的内角和定理的推导
一、复习导入,明确目标(3分钟)
1、什么是三角形?
2、什么是三角形的内角?
3、三角形的内角和是多少?
二、任务驱动,分步探究 探究点一:多边形的有关概念
预习课本83-84页,思考问题
你能仿照三角形的定义说出四边形、五边形的概念吗?
n边形的概念呢
观察下面多边形,它们的边,角有什么特点?
在平面内,内角都相等,边也都相等的多边形叫做正多边形
例1:下列说法中,正确的是( )
(1)三角形是边数最少的多边形
(2)由n条线段连接起来组成的图形叫做多边形
(3)n边形有n条边、n个顶点、2n个内角
A、 0个 B、1个 C、2个 D、3个
例2:下列说法(1)等腰三角形是正多边形;(2)等边三角形是正多边形;(3)长方形是正多边形;(4)正方形是正多边形。其中正确的个数为( )
A、 1个 B、2个 C、3个 D、4个
探究点二:多边形的内角和
具体任务:阅读课本第84--85页
思考:
1、三角形的内角和随三角形的形状大小而变化吗?
2、通过作对角线可以把四边形转化为三角形吗?五边形呢?六边形呢?......
3、过多边形的一个顶点能作多少条对角线?把多边形分成多少个三角形?
观察下列图形,从多边形的一个顶点出发可以引多少条对角线?这些对角线把多边形分成几个三角形?你能猜想 n 边形的内角和是多少度吗?
例3、求九边形的内角和
解:九边形的内角和为
(n-2)×180°=(9-2)×180°=1260°
例4、一个多边形的内角和等于2340°,求它的边数
解:设这个多边形的边数为n,根据题意,得
(n-2)×180°=2340°
解得 n=15
即这个多边形的边数为15
三、巩固练习,拓展提高
1、若一个多边形从一个顶点可以引5条对角线,则它
是( )
A、五边形 B、六边形 C、七边形 D、八边形
2、下列角度中,不能成为多边形内角和的是( )
A、600° B、720° C、900° D、1800°
3、若一个多边形的每一个内角都等于144o ,求它的
边数。(提示:正多边形的内角都相等)
解:设这个多边形的边数为n,根据题意,得
(n-2)?180°=n144°, 解得n=10.
所以这个多边形的边数是10
课堂小结,回扣目标
三角形、四边形都属于多边形,所以四 边形的定义、边、顶点、内角、内角和等概念可类比地扩展到多边形。
、n边形的内角和为(n-2) ×180°(n≥3)
中考链接
(广东中考)一个多边形的内角和是900°,这个多边形的边数是( )
A、10 B、9 C、8 D、7
五、达标检测(10分钟,共10分)
姓名 班级 小组
八边形的内角和是( )
A、1440° B、1260° C、1080° D、900°
2、四边形的内角的度数之比为2∶3∶5∶8, 则各个角的度数分别是
3、一个多边形的内角和比四边形内角和的3倍多180°,则这个多边形的边数是
4、已知多边形的每一内角为150°,求这个多边形的边数.
学(教)后反思:
我的收获是: ________________________________________________
我的问题是: _____________________________________________
