(期末复习精炼)人教版数学九年级上册课件:第二十二章二次函数复习课件(56张PPT)
文档属性
| 名称 | (期末复习精炼)人教版数学九年级上册课件:第二十二章二次函数复习课件(56张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 778.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-31 00:00:00 | ||
图片预览









文档简介
课件56张PPT。第二十二章 二次函数本章知识梳理考纲要求1. 通过对实际问题情境的分析,体会二次函数的意义.
2. 会用描点法画出二次函数的图象,能通过图象了解二次函数的性质.
3. 会用配方法将数字系数的二次函数的表达式化为y=a(x-h)2+k(a≠0)的形式,并能由此得到二次函数图象的顶点坐标、开口方向,画出图象的对称轴,并能解决简单实际问题.
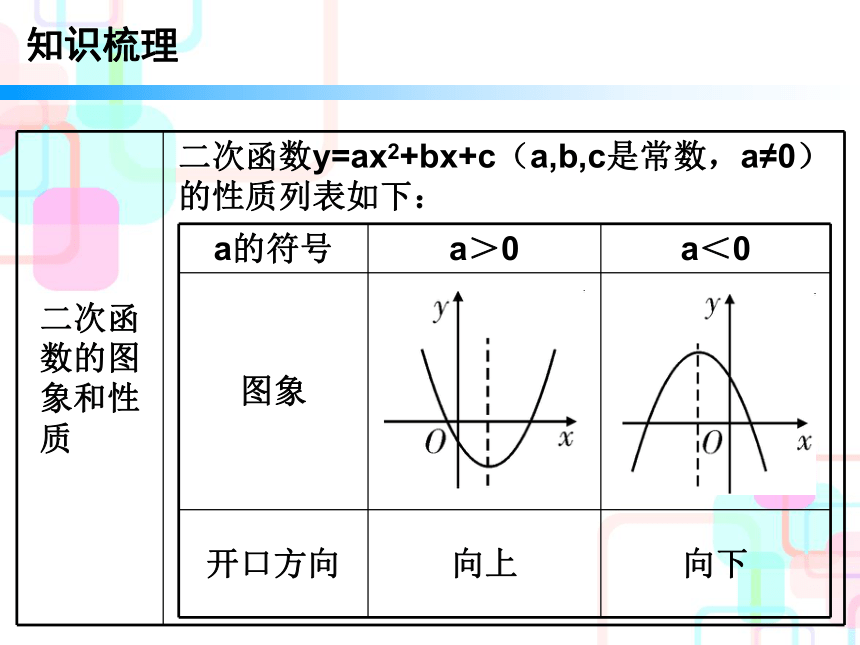
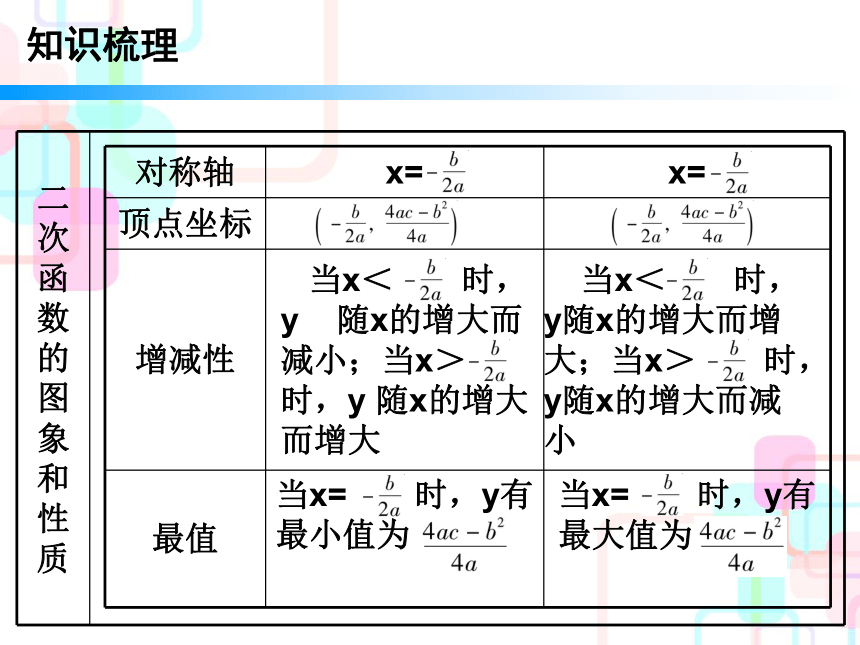
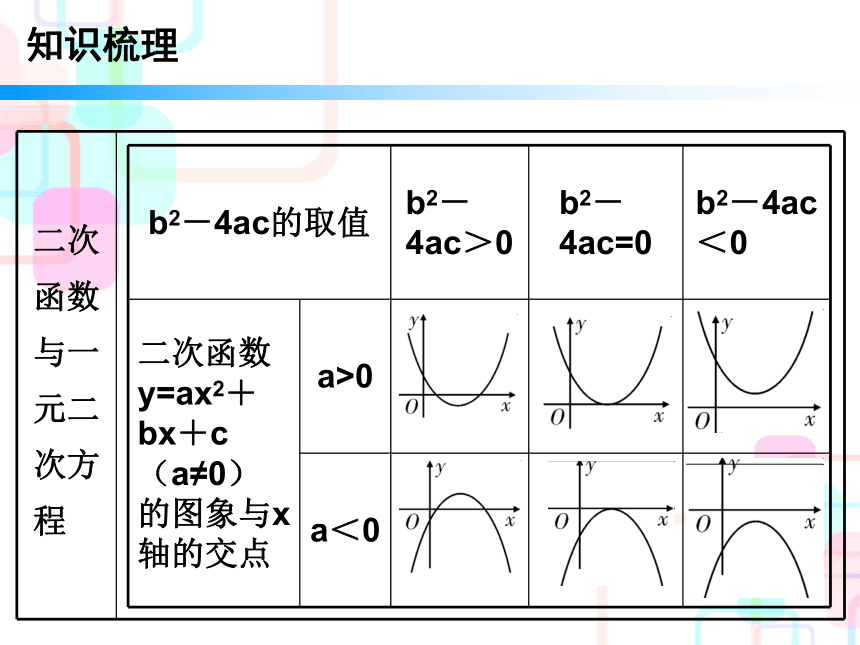
4. 会利用二次函数的图象求一元二次方程的近似解. 知识梳理知识梳理知识梳理知识梳理知识梳理易错点
一、配方时,不能直接除去(或丢掉)二次项系数,同时在提出二次项系数后,不能在括号内加,同时在括号外减去所加的常数.
【例1】求二次函数y=-2x2+8x-2图象的顶点坐标.
易错提示:配方时,学生喜欢粗心地在右边将二次项系数-2除掉,得到y=x2-4x+1,然后再得到y=(x-2)2-3,或出现y=-2x2+8x-2=-2(x2-4x)-2=-2(x2-4x+4)-2-4的变形错误. 本章易错点归总
正解:y=-2x2+8x-2
=-2(x2-4x)-2
=-2(x2-4x+4-4)-2
=-2(x-2)2+6.
∴二次函数y=-2x2+8x-2图象的顶点坐标为(2,6). 本章易错点归总二、对于抛物线的平移问题,要么对“括号内左加右减,括号外上加下减”掌握不透,导致图象的平移方向出错,要么未将一般式化为顶点式,而将平移规律直接错误地运用到一般式中.
【例2】将抛物线y=-x2+2x向左平移2个单位后,得到的抛物线的解析式是什么?本章易错点归总本章易错点归总易错提示:学生容易混淆平移方向,出现y=-x2+2x+2,y=-x2+2x-2,y=-(x+2)2+2x或y=-(x-2)2+2x等错误. 正解:抛物线的平移可以看作是顶点移动,先需配方得y=-(x-1)2+1,再根据“括号内左加”得到y=-(x-1+2)2+1,即y=-(x+1)2+1.三、对于含有字母系数的函数,要仔细审题,分类讨论,合理取舍,寻求准确答案.
【例3】当a为何值时,函数y=ax2-3x+1的图象与x轴只有一个交点?
易错提示:学生易受思维定式的影响,主观臆断此函数一定是二次函数,出现只考虑Δ=0的情形,从而导致答案不全. 本章易错点归总本章易错点归总
正解:当a=0时,函数为y=-3x+1,此一次函数与x轴有一个交点;当a≠0时,此函数为二次函数,当Δ=(-3)2-4a=0,即a= 时,函数图象与x轴只有一个交点.
综上所述,当a=0或 时,函数y=ax2-3x+1的图象与x轴只有一个交点. 四、利用二次函数模型解决实际问题时,忽略所得二次函数中自变量的取值范围,将实际问题的图象看成了一条完整的抛物线,导致所求的解不符合实际问题的意义.
【例4】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯. 已知这种节能灯的成本价为每件10元,出厂本章易错点归总价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?(物价部门规定,这种节能灯的销售单价不得高于25元)本章易错点归总易错提示:解答第(2)小题时,配方得W=(x-10)(-10x+500)=-10(x-30)2+4 000,得到当x=30元时,每月可获得最大利润4 000元,这是由于学生受解题习惯影响,忽略了“销售单价不得高于25元”的条件限制而造成了错误. 本章易错点归总正解:(1)当x=20时,
y=-10x+500=-10×20+500=300,
300×(12-10)=300×2=600(元).
∴政府这个月为他承担的总差价为600元. (2)依题意,得
W=(x-10)(-10x+500)=-10x2+600x-5 000
=-10(x-30)2+4 000.
∵a=-10<0,
∴当x<30时,W随x的增大而增大.
又∵x≤25,∴当x=25时,W有最大值为
-10×(25-30)2+4 000=3 750(元).
∴当销售单价定为25元时,每月可获得最大利润3 750元. 本章易错点归总本章易错点归总学以致用
1. 用配方法求y=2x2-8x-10的对称轴和顶点坐标. 解:由题意,得y=2x2-8x-10=2(x-2)2-18,
∴对称轴为直线x=2,顶点坐标为(2,-18). 本章易错点归总2. (2017贵港)将如图M22-1所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线解析式是( )
A. y=(x-1)2+1
B. y=(x+1)2+1
C. y=2(x-1)2+1
D. y=2(x+1)2+1C本章易错点归总3. 已知函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )
A. k<4 B. k≤4
C. k<4且k≠3 D. k≤4且k≠3B本章易错点归总4. (2017营口)夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务. 为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第x天生产空调y台,直接写出y与x之间的函数解析式,并写出自变量x的取值范围;本章易错点归总(2)若每台空调的成本价(日生产量不超过50台时)为2 000元,订购价格为每台2 920元,设第x天的利润为W元,试求W与x之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少. 解:(1)∵接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,
∴由题意,得第x天生产空调y台,y与x之间的函数解析式为y=40+2x(1≤x≤10).本章易错点归总(2)当1≤x≤5时,W=(2 920-2 000)×(40+2x)=1 840x+36 800,
∵1 840>0,∴W随x的增大而增大.
∴当x=5时,W最大=1 840×5+36 800=46 000;
当5<x≤10时,W=[2 920-2 000-20(40+2x-50)]×(40+2x)=-80(x-4)2+46 080.
此时函数图象开口向下,在对称轴右侧,W随着x的增大而减小,本章易错点归总又∵天数x为整数,
∴当x=6时,W最大值=45 760元.
综上所述,
∵46 000>45 760,
∴当x=5时,W最大,且W最大值=46 000元.考点1 二次函数的定义、图像和性质一、二次函数的定义
1. 下列函数中,y是关于x的二次函数的是( )
A. y=x3+2x2+3 B. y=
C. y=x2+x D. y=mx2+x+1
2. 若函数y=(m-1)x2+3x+1是二次函数,则有
( )
A. m≠0 B. m≠1
C. x≠0 D. x≠1BC二、二次函数的图象
3. 二次函数y=-x2-2x+3的图象大致是( )考点1 二次函数的定义、图像和性质A4. 函数y=ax2(a≠0)和y=-ax+b(a≠0)在同一坐标系中的图象可能为( )考点1 二次函数的定义、图像和性质D三、二次函数的性质
5. 抛物线y=x2-4x-3的顶点坐标为( )
A. (2,-7) B. (2,7)
C. (-2,-7) D. (-2,7)
6. 下列关于抛物线y=-x2+2的说法正确的是( )
A. 抛物线开口向上
B. 顶点坐标为(-1,2)
C. 在对称轴的右侧,y随x的增大而增大
D. 抛物线与x轴有两个交点考点1 二次函数的定义、图像和性质DA7. 当-4≤x≤2时,函数y=-(x+3)2+2的取值范围为
( )
A. -23≤y≤1 B. -23≤y≤2
C. -7≤y≤1 D. -34≤y≤2考点1 二次函数的定义、图像和性质B8. 二次函数y=ax2+bx+c(a≠0)的图象如图M22-2所示,对于下列结论:①a<0;②b<0;③c>0;④2a+b=0;⑤a-b+c<0,其中正确的有( )
A. 4个
B. 3个
C. 2个
D. 1个考点1 二次函数的定义、图像和性质A9. 对于抛物线y=(x+1)2+3有以下结论:①抛物线开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小. 其中正确结论有( )
A. 1个 B. 2个
C. 3个 D. 4个考点1 二次函数的定义、图像和性质A10. 如图M22-3,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象过正方形ABOC的三个顶点A,B,C,则ac的值是________. 考点1 二次函数的定义、图像和性质-2考点2 用待定系数法求二次函数的解析式一、一般式
1. 抛物线y=ax2+bx+c经过(0,5),(2,2),(-8,-3)三点,求它的开口方向、对称轴和顶点坐标. 解:∵抛物线y=ax2+bx+c经过(0,5),(2,2),(-8,-3)三点,
∴c=5, 4a+2b+c=2, 64a-8b+c=-3.
解得a= ,b=-1,c=5.
∴y= x2-x+5= (x+2)2+6.
∴该抛物线的开口向下,对称轴是直线x=-2,顶点坐标为(-2,6).二、顶点式
2. 抛物线的顶点坐标为(1,3),且过点(2,1),求抛物线对应的二次函数表达式. 考点2 用待定系数法求二次函数的解析式解:设抛物线的解析式为y=a(x-1)2+3,把(2,1)代入,得a·(2-1)2+3=1.
解得a=-2.
所以抛物线的解析式为y=-2(x-1)2+3. 三、交点式
3. 已知二次函数图象经过点A(-3,0),B(1,0),C(0,-3),求此二次函数的解析式. 考点2 用待定系数法求二次函数的解析式解:设抛物线的解析式为y=a(x+3)(x-1),把C(0,-3)代入,得a·3· (-1)=-3.
解得a=1.
所以抛物线解析式为y=(x+3)(x-1),即y=x2+2x-3.四、综合
4. 若抛物线y=-x2+bx+c经过点A(2,0),B(0,2).
(1)求这条抛物线的解析式;
(2)如图M22-4,点P是抛物线上一动点,连接BP,OP,若△BOP是以BO为底边的
等腰三角形,求点P的坐标. 考点2 用待定系数法求二次函数的解析式考点2 用待定系数法求二次函数的解析式解:(1)将点A(2,0),B(0,2)代入y=-x2+bx+c,得-4+2b+c=0,c=2.解得b=1,c=2.
∴这条抛物线的解析式为y=-x2+x+2.
(2)∵△BOP是以BO为底边的等腰三角形,且OB=2,
∴点P的纵坐标为1. 当y=1时,-x2+x+2=1.
解得x1= ,x2=
∴点P的坐标为 或5. 如图M22-5,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连接AM,BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由. 考点2 用待定系数法求二次函数的解析式解:(1)∵点A为直线y=x+1与x轴的交点,
∴A(-1,0).
又点B的横坐标为2,代入y=x+1,得y=3,
∴B(2,3).
∵抛物线顶点在y轴上,
∴可设抛物线的解析式为y=ax2+c.
把A,B两点坐标代入,得a+c=0,4a+c=3.
解得a=1,c=-1.
∴抛物线的解析式为y=x2-1. 考点2 用待定系数法求二次函数的解析式
(2)△ABM为直角三角形. 理由如下:由(1)知抛物线的解析式为y=x2-1,可得点M的坐标为(0,-1),
∴AM2=12+12=2,AB2=(2+1)2+32=18,BM2=22+(3+1)2=20.
∴AM2+AB2=2+18=20=BM2.
∴△ABM为直角三角形.考点2 用待定系数法求二次函数的解析式考点3 二次函数与一元二次方程一、抛物线与坐标轴的交点
1. 若二次函数的解析式为y=2x2-4x+3,则函数图象与x轴交点的情况是( )
A. 没有交点 B. 有一个交点
C. 有两个交点 D. 以上都不对A考点3 二次函数与一元二次方程2. 已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A. x1=1,x2=-1 B. x1=1,x2=2
C. x1=1,x2=0 D. x1=1,x2=3B考点3 二次函数与一元二次方程3. 如图M22-6,抛物线y=ax2+bx+c(a≠0)与x轴的一个交点为(-2,0),对称轴为直线x=1,则y<0时x的取值范围是( )
A. x>4或x<-2
B. -2<x<4
C. -2<x<3
D. 0<x<3 B考点3 二次函数与一元二次方程4. 已知抛物线y=a(x-1)(x-2)经过点(-1,3),利用其函数图象判断函数y的值大于0时,x的取值范围为( )
A. x>2或x<1 B. 1<x<2
C. x>-1或x<-2 D. -2<x<-1A考点3 二次函数与一元二次方程5. (2017镇江)若二次函数y=x2-4x+n的图象与x轴只有一个公共点,则实数n=________.
6. 抛物线y=ax2+bx+c的部分图象如图M22-7所示,则关于x的不等式ax2+bx+c+2>0的解集为___________.4-4<x<2考点3 二次函数与一元二次方程7. 已知,如图M22-8,二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,
求出PA+PD的最小值;
(3)若抛物线上有一动点M,
使△ABM的面积为6,求点M的坐标. 考点3 二次函数与一元二次方程解:(1)∵二次函数y=x2+bx+c的图象经过点A(-3,0),D(-2,-3),
∴9-3b+c=0, 4-2b+c=-3.解得b=2,c=-3.
∴二次函数的解析式为y=x2+2x-3.
(2)∵抛物线的对称轴是直线
x=-1,D(-2,-3),C(0,-3),
∴C,D关于抛物线的对称轴直线x=-1对称,如答图M22-1所示,连接AC,与对称轴的交点就是点P,此时PA+PD=PA+PC=AC=考点3 二次函数与一元二次方程(3)设点M的坐标为(m,m2+2m-3).
令y=0,即x2+2x-3=0.解得x=-3或x=1.
∴点B的坐标为(1,0). ∴AB=4.
∵S△MAB=6,∴ =6.
∴m2+2m=0或m2+2m=6.
∴m=0或-2或-1+ 或-1- .
∴点P的坐标为(0,-3)或(-2,-3)或(-1+ ,3)或(-1- ,3).考点3 二次函数与一元二次方程二、图象法求一元二次方程的近似根
8. (2017兰州)下表是一组二次函数y=x2+3x-5的自变量x与函数值y的对应值:
那么方程x2+3x-5=0的一个近似根是( )
A. 1 B. 1.1
C. 1.2 D. 1.3C考点4 实际问题与二次函数一、图形面积问题
1. 如图M22-9,在矩形ABCD中,AB=6 cm,BC=12 cm,点P从点A出发,沿AB边向点B以1 cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2 cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动. 设△PQD的面积为S,点移动的时间为x(x>0)s.考点4 实际问题与二次函数(1)求S关于x的函数表达式及自变量x的取值范围;
(2)经过多少时间,△PQD的面积最小?解:(1)根据题意,得AP=x,BQ=2x,则
BP=6-x,CQ=12-2x,
∴S△PQD=S矩形ABCD-S△APD-S△PBQ-S△CDQ=12×6-
×12x- ·2x(6-x)- ×6(12-2x)=x2-6x+36. ∴S=x2-6x+36(0<x≤6).
(2)∵S=x2-6x+36=(x-3)2+27,
∴当x=3时,S最小,即经过3 s时,△PQD的面积最小. 二、商品利润问题
2. 为满足市场需求,某超市在五月初五端午节来临前夕,购进一种品牌粽子,每盒进价是40元,超市规定每盒售价不得少于45元. 根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;考点4 实际问题与二次函数(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?考点4 实际问题与二次函数解:(1)由题意,得y=700-20(x-45)=-20x+1 600.
(2)P=(x-40)(-20x+1 600)=-20x2+2 400x-64 000=-20(x-60)2+8 000,
∵x≥45,a=-20<0,
∴当x=60时,P最大值=8 000(元),
即当每盒售价定为60元时,每天销售的利润P最大,最大利润是8 000元. 三、实物抛物线问题
3. 如图M22-10,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=
,则该运动员此次掷铅球的成绩是( )
A. 6 m B. 12 m
C. 8 m D. 10 m考点4 实际问题与二次函数D4. (2017德州)随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,如图M22-11,在水池中心竖直安装了一根高为2 m的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为1 m处达到最高,水柱落地处离池中心3 m.
(1)请你建立适当的平面直角坐标系,
并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度.考点4 实际问题与二次函数考点4 实际问题与二次函数解:(1)如答图M22-2所示,以水管与地面交点为原点,原点与水柱落地点所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系.
设抛物线的解析式为y=a(x-1)2+h,代入(3,0)和(0,2),得4a+h=0,a+h=2.
解得a= ,h= .
∴抛物线的解析式为y= (x-1)2+ ,
即y= x2+ x+2(0≤x≤3).
(2)由y= (x-1)2+ (0≤x≤3),得当x=1时,y= ,即水柱的最大高度为 m.
2. 会用描点法画出二次函数的图象,能通过图象了解二次函数的性质.
3. 会用配方法将数字系数的二次函数的表达式化为y=a(x-h)2+k(a≠0)的形式,并能由此得到二次函数图象的顶点坐标、开口方向,画出图象的对称轴,并能解决简单实际问题.
4. 会利用二次函数的图象求一元二次方程的近似解. 知识梳理知识梳理知识梳理知识梳理知识梳理易错点
一、配方时,不能直接除去(或丢掉)二次项系数,同时在提出二次项系数后,不能在括号内加,同时在括号外减去所加的常数.
【例1】求二次函数y=-2x2+8x-2图象的顶点坐标.
易错提示:配方时,学生喜欢粗心地在右边将二次项系数-2除掉,得到y=x2-4x+1,然后再得到y=(x-2)2-3,或出现y=-2x2+8x-2=-2(x2-4x)-2=-2(x2-4x+4)-2-4的变形错误. 本章易错点归总
正解:y=-2x2+8x-2
=-2(x2-4x)-2
=-2(x2-4x+4-4)-2
=-2(x-2)2+6.
∴二次函数y=-2x2+8x-2图象的顶点坐标为(2,6). 本章易错点归总二、对于抛物线的平移问题,要么对“括号内左加右减,括号外上加下减”掌握不透,导致图象的平移方向出错,要么未将一般式化为顶点式,而将平移规律直接错误地运用到一般式中.
【例2】将抛物线y=-x2+2x向左平移2个单位后,得到的抛物线的解析式是什么?本章易错点归总本章易错点归总易错提示:学生容易混淆平移方向,出现y=-x2+2x+2,y=-x2+2x-2,y=-(x+2)2+2x或y=-(x-2)2+2x等错误. 正解:抛物线的平移可以看作是顶点移动,先需配方得y=-(x-1)2+1,再根据“括号内左加”得到y=-(x-1+2)2+1,即y=-(x+1)2+1.三、对于含有字母系数的函数,要仔细审题,分类讨论,合理取舍,寻求准确答案.
【例3】当a为何值时,函数y=ax2-3x+1的图象与x轴只有一个交点?
易错提示:学生易受思维定式的影响,主观臆断此函数一定是二次函数,出现只考虑Δ=0的情形,从而导致答案不全. 本章易错点归总本章易错点归总
正解:当a=0时,函数为y=-3x+1,此一次函数与x轴有一个交点;当a≠0时,此函数为二次函数,当Δ=(-3)2-4a=0,即a= 时,函数图象与x轴只有一个交点.
综上所述,当a=0或 时,函数y=ax2-3x+1的图象与x轴只有一个交点. 四、利用二次函数模型解决实际问题时,忽略所得二次函数中自变量的取值范围,将实际问题的图象看成了一条完整的抛物线,导致所求的解不符合实际问题的意义.
【例4】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯. 已知这种节能灯的成本价为每件10元,出厂本章易错点归总价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?(物价部门规定,这种节能灯的销售单价不得高于25元)本章易错点归总易错提示:解答第(2)小题时,配方得W=(x-10)(-10x+500)=-10(x-30)2+4 000,得到当x=30元时,每月可获得最大利润4 000元,这是由于学生受解题习惯影响,忽略了“销售单价不得高于25元”的条件限制而造成了错误. 本章易错点归总正解:(1)当x=20时,
y=-10x+500=-10×20+500=300,
300×(12-10)=300×2=600(元).
∴政府这个月为他承担的总差价为600元. (2)依题意,得
W=(x-10)(-10x+500)=-10x2+600x-5 000
=-10(x-30)2+4 000.
∵a=-10<0,
∴当x<30时,W随x的增大而增大.
又∵x≤25,∴当x=25时,W有最大值为
-10×(25-30)2+4 000=3 750(元).
∴当销售单价定为25元时,每月可获得最大利润3 750元. 本章易错点归总本章易错点归总学以致用
1. 用配方法求y=2x2-8x-10的对称轴和顶点坐标. 解:由题意,得y=2x2-8x-10=2(x-2)2-18,
∴对称轴为直线x=2,顶点坐标为(2,-18). 本章易错点归总2. (2017贵港)将如图M22-1所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线解析式是( )
A. y=(x-1)2+1
B. y=(x+1)2+1
C. y=2(x-1)2+1
D. y=2(x+1)2+1C本章易错点归总3. 已知函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )
A. k<4 B. k≤4
C. k<4且k≠3 D. k≤4且k≠3B本章易错点归总4. (2017营口)夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务. 为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第x天生产空调y台,直接写出y与x之间的函数解析式,并写出自变量x的取值范围;本章易错点归总(2)若每台空调的成本价(日生产量不超过50台时)为2 000元,订购价格为每台2 920元,设第x天的利润为W元,试求W与x之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少. 解:(1)∵接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,
∴由题意,得第x天生产空调y台,y与x之间的函数解析式为y=40+2x(1≤x≤10).本章易错点归总(2)当1≤x≤5时,W=(2 920-2 000)×(40+2x)=1 840x+36 800,
∵1 840>0,∴W随x的增大而增大.
∴当x=5时,W最大=1 840×5+36 800=46 000;
当5<x≤10时,W=[2 920-2 000-20(40+2x-50)]×(40+2x)=-80(x-4)2+46 080.
此时函数图象开口向下,在对称轴右侧,W随着x的增大而减小,本章易错点归总又∵天数x为整数,
∴当x=6时,W最大值=45 760元.
综上所述,
∵46 000>45 760,
∴当x=5时,W最大,且W最大值=46 000元.考点1 二次函数的定义、图像和性质一、二次函数的定义
1. 下列函数中,y是关于x的二次函数的是( )
A. y=x3+2x2+3 B. y=
C. y=x2+x D. y=mx2+x+1
2. 若函数y=(m-1)x2+3x+1是二次函数,则有
( )
A. m≠0 B. m≠1
C. x≠0 D. x≠1BC二、二次函数的图象
3. 二次函数y=-x2-2x+3的图象大致是( )考点1 二次函数的定义、图像和性质A4. 函数y=ax2(a≠0)和y=-ax+b(a≠0)在同一坐标系中的图象可能为( )考点1 二次函数的定义、图像和性质D三、二次函数的性质
5. 抛物线y=x2-4x-3的顶点坐标为( )
A. (2,-7) B. (2,7)
C. (-2,-7) D. (-2,7)
6. 下列关于抛物线y=-x2+2的说法正确的是( )
A. 抛物线开口向上
B. 顶点坐标为(-1,2)
C. 在对称轴的右侧,y随x的增大而增大
D. 抛物线与x轴有两个交点考点1 二次函数的定义、图像和性质DA7. 当-4≤x≤2时,函数y=-(x+3)2+2的取值范围为
( )
A. -23≤y≤1 B. -23≤y≤2
C. -7≤y≤1 D. -34≤y≤2考点1 二次函数的定义、图像和性质B8. 二次函数y=ax2+bx+c(a≠0)的图象如图M22-2所示,对于下列结论:①a<0;②b<0;③c>0;④2a+b=0;⑤a-b+c<0,其中正确的有( )
A. 4个
B. 3个
C. 2个
D. 1个考点1 二次函数的定义、图像和性质A9. 对于抛物线y=(x+1)2+3有以下结论:①抛物线开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小. 其中正确结论有( )
A. 1个 B. 2个
C. 3个 D. 4个考点1 二次函数的定义、图像和性质A10. 如图M22-3,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象过正方形ABOC的三个顶点A,B,C,则ac的值是________. 考点1 二次函数的定义、图像和性质-2考点2 用待定系数法求二次函数的解析式一、一般式
1. 抛物线y=ax2+bx+c经过(0,5),(2,2),(-8,-3)三点,求它的开口方向、对称轴和顶点坐标. 解:∵抛物线y=ax2+bx+c经过(0,5),(2,2),(-8,-3)三点,
∴c=5, 4a+2b+c=2, 64a-8b+c=-3.
解得a= ,b=-1,c=5.
∴y= x2-x+5= (x+2)2+6.
∴该抛物线的开口向下,对称轴是直线x=-2,顶点坐标为(-2,6).二、顶点式
2. 抛物线的顶点坐标为(1,3),且过点(2,1),求抛物线对应的二次函数表达式. 考点2 用待定系数法求二次函数的解析式解:设抛物线的解析式为y=a(x-1)2+3,把(2,1)代入,得a·(2-1)2+3=1.
解得a=-2.
所以抛物线的解析式为y=-2(x-1)2+3. 三、交点式
3. 已知二次函数图象经过点A(-3,0),B(1,0),C(0,-3),求此二次函数的解析式. 考点2 用待定系数法求二次函数的解析式解:设抛物线的解析式为y=a(x+3)(x-1),把C(0,-3)代入,得a·3· (-1)=-3.
解得a=1.
所以抛物线解析式为y=(x+3)(x-1),即y=x2+2x-3.四、综合
4. 若抛物线y=-x2+bx+c经过点A(2,0),B(0,2).
(1)求这条抛物线的解析式;
(2)如图M22-4,点P是抛物线上一动点,连接BP,OP,若△BOP是以BO为底边的
等腰三角形,求点P的坐标. 考点2 用待定系数法求二次函数的解析式考点2 用待定系数法求二次函数的解析式解:(1)将点A(2,0),B(0,2)代入y=-x2+bx+c,得-4+2b+c=0,c=2.解得b=1,c=2.
∴这条抛物线的解析式为y=-x2+x+2.
(2)∵△BOP是以BO为底边的等腰三角形,且OB=2,
∴点P的纵坐标为1. 当y=1时,-x2+x+2=1.
解得x1= ,x2=
∴点P的坐标为 或5. 如图M22-5,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连接AM,BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由. 考点2 用待定系数法求二次函数的解析式解:(1)∵点A为直线y=x+1与x轴的交点,
∴A(-1,0).
又点B的横坐标为2,代入y=x+1,得y=3,
∴B(2,3).
∵抛物线顶点在y轴上,
∴可设抛物线的解析式为y=ax2+c.
把A,B两点坐标代入,得a+c=0,4a+c=3.
解得a=1,c=-1.
∴抛物线的解析式为y=x2-1. 考点2 用待定系数法求二次函数的解析式
(2)△ABM为直角三角形. 理由如下:由(1)知抛物线的解析式为y=x2-1,可得点M的坐标为(0,-1),
∴AM2=12+12=2,AB2=(2+1)2+32=18,BM2=22+(3+1)2=20.
∴AM2+AB2=2+18=20=BM2.
∴△ABM为直角三角形.考点2 用待定系数法求二次函数的解析式考点3 二次函数与一元二次方程一、抛物线与坐标轴的交点
1. 若二次函数的解析式为y=2x2-4x+3,则函数图象与x轴交点的情况是( )
A. 没有交点 B. 有一个交点
C. 有两个交点 D. 以上都不对A考点3 二次函数与一元二次方程2. 已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A. x1=1,x2=-1 B. x1=1,x2=2
C. x1=1,x2=0 D. x1=1,x2=3B考点3 二次函数与一元二次方程3. 如图M22-6,抛物线y=ax2+bx+c(a≠0)与x轴的一个交点为(-2,0),对称轴为直线x=1,则y<0时x的取值范围是( )
A. x>4或x<-2
B. -2<x<4
C. -2<x<3
D. 0<x<3 B考点3 二次函数与一元二次方程4. 已知抛物线y=a(x-1)(x-2)经过点(-1,3),利用其函数图象判断函数y的值大于0时,x的取值范围为( )
A. x>2或x<1 B. 1<x<2
C. x>-1或x<-2 D. -2<x<-1A考点3 二次函数与一元二次方程5. (2017镇江)若二次函数y=x2-4x+n的图象与x轴只有一个公共点,则实数n=________.
6. 抛物线y=ax2+bx+c的部分图象如图M22-7所示,则关于x的不等式ax2+bx+c+2>0的解集为___________.4-4<x<2考点3 二次函数与一元二次方程7. 已知,如图M22-8,二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,
求出PA+PD的最小值;
(3)若抛物线上有一动点M,
使△ABM的面积为6,求点M的坐标. 考点3 二次函数与一元二次方程解:(1)∵二次函数y=x2+bx+c的图象经过点A(-3,0),D(-2,-3),
∴9-3b+c=0, 4-2b+c=-3.解得b=2,c=-3.
∴二次函数的解析式为y=x2+2x-3.
(2)∵抛物线的对称轴是直线
x=-1,D(-2,-3),C(0,-3),
∴C,D关于抛物线的对称轴直线x=-1对称,如答图M22-1所示,连接AC,与对称轴的交点就是点P,此时PA+PD=PA+PC=AC=考点3 二次函数与一元二次方程(3)设点M的坐标为(m,m2+2m-3).
令y=0,即x2+2x-3=0.解得x=-3或x=1.
∴点B的坐标为(1,0). ∴AB=4.
∵S△MAB=6,∴ =6.
∴m2+2m=0或m2+2m=6.
∴m=0或-2或-1+ 或-1- .
∴点P的坐标为(0,-3)或(-2,-3)或(-1+ ,3)或(-1- ,3).考点3 二次函数与一元二次方程二、图象法求一元二次方程的近似根
8. (2017兰州)下表是一组二次函数y=x2+3x-5的自变量x与函数值y的对应值:
那么方程x2+3x-5=0的一个近似根是( )
A. 1 B. 1.1
C. 1.2 D. 1.3C考点4 实际问题与二次函数一、图形面积问题
1. 如图M22-9,在矩形ABCD中,AB=6 cm,BC=12 cm,点P从点A出发,沿AB边向点B以1 cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2 cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动. 设△PQD的面积为S,点移动的时间为x(x>0)s.考点4 实际问题与二次函数(1)求S关于x的函数表达式及自变量x的取值范围;
(2)经过多少时间,△PQD的面积最小?解:(1)根据题意,得AP=x,BQ=2x,则
BP=6-x,CQ=12-2x,
∴S△PQD=S矩形ABCD-S△APD-S△PBQ-S△CDQ=12×6-
×12x- ·2x(6-x)- ×6(12-2x)=x2-6x+36. ∴S=x2-6x+36(0<x≤6).
(2)∵S=x2-6x+36=(x-3)2+27,
∴当x=3时,S最小,即经过3 s时,△PQD的面积最小. 二、商品利润问题
2. 为满足市场需求,某超市在五月初五端午节来临前夕,购进一种品牌粽子,每盒进价是40元,超市规定每盒售价不得少于45元. 根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;考点4 实际问题与二次函数(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?考点4 实际问题与二次函数解:(1)由题意,得y=700-20(x-45)=-20x+1 600.
(2)P=(x-40)(-20x+1 600)=-20x2+2 400x-64 000=-20(x-60)2+8 000,
∵x≥45,a=-20<0,
∴当x=60时,P最大值=8 000(元),
即当每盒售价定为60元时,每天销售的利润P最大,最大利润是8 000元. 三、实物抛物线问题
3. 如图M22-10,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=
,则该运动员此次掷铅球的成绩是( )
A. 6 m B. 12 m
C. 8 m D. 10 m考点4 实际问题与二次函数D4. (2017德州)随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,如图M22-11,在水池中心竖直安装了一根高为2 m的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为1 m处达到最高,水柱落地处离池中心3 m.
(1)请你建立适当的平面直角坐标系,
并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度.考点4 实际问题与二次函数考点4 实际问题与二次函数解:(1)如答图M22-2所示,以水管与地面交点为原点,原点与水柱落地点所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系.
设抛物线的解析式为y=a(x-1)2+h,代入(3,0)和(0,2),得4a+h=0,a+h=2.
解得a= ,h= .
∴抛物线的解析式为y= (x-1)2+ ,
即y= x2+ x+2(0≤x≤3).
(2)由y= (x-1)2+ (0≤x≤3),得当x=1时,y= ,即水柱的最大高度为 m.
同课章节目录
