沪科版九年级数学上册第22章相似形单元检测试卷含答案
文档属性
| 名称 | 沪科版九年级数学上册第22章相似形单元检测试卷含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 167.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-31 00:00:00 | ||
图片预览



文档简介
沪科版九年级上册 第22章 相似形 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.若,则
A. B. C. D.
?2.已知是线段的黄金分割点,且,,则长约为( )
A. B. C. D.
?3.如图,两个位似图形和,若,则正确的是( )
A. B.
C. D.
?4.如果线段,,那么和的比例中项是( )
A. B. C. D.
?5.如图,中,交于点,交于点,如果,那么下列等式成立的是( )
A. B.
C. D.
?6.顶角为的等腰三角形称为黄金三角形,如图,五边形的条边相等,个内角相等,则图中共有黄金三角形的个数是( )
A. B. C. D.
?7.如图所示,顶角为的等腰三角形,其底边与腰之比等于,这样的三角形叫黄金三角形,已知腰长,为第一个黄金三角形,为第二个黄金三角形,为第三个黄金三角形,以此类推,第个黄金三角形的周长为( )
A. B.
C. D.
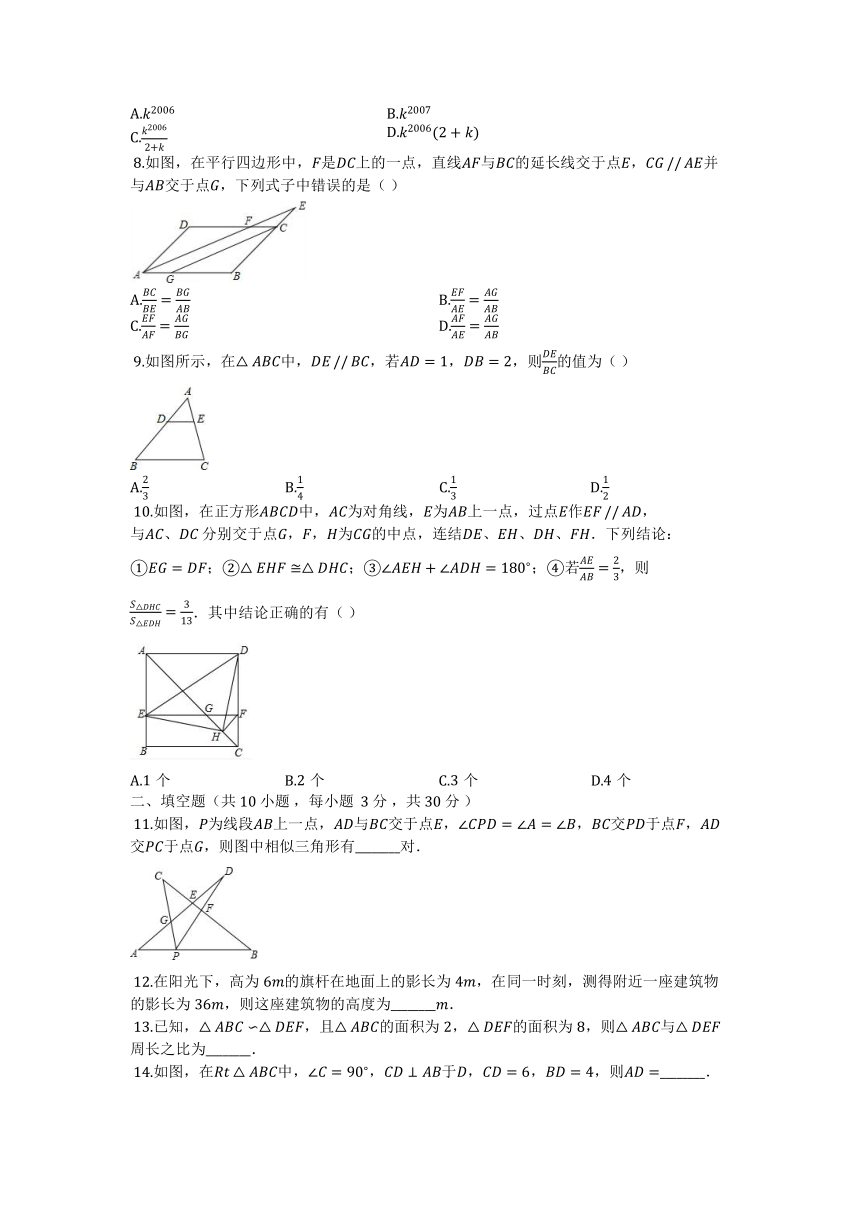
?8.如图,在平行四边形中,是上的一点,直线与的延长线交于点,并与交于点,下列式子中错误的是( )
A. B.
C. D.
?9.如图所示,在中,,若,,则的值为( )
A. B. C. D.
?10.如图,在正方形中,为对角线,为上一点,过点作,与、?分别交于点,,为的中点,连结、、、.下列结论:①;②;③;④若,则.其中结论正确的有( )
A.个 B.个 C.个 D.个
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,为线段上一点,与交于点,,交于点,交于点,则图中相似三角形有________对.
?12.在阳光下,高为的旗杆在地面上的影长为,在同一时刻,测得附近一座建筑物的影长为,则这座建筑物的高度为________.
?13.已知,,且的面积为,的面积为,则与周长之比为________.
?14.如图,在中,,于,,,则________.
?15.如图,已知中,,连接,的面积是面积的,则________.
?
16.在中,已知点、分别在边、上,如果,,,,,那么________.
?17.如图,正方形和正方形是位似形,点的坐标为,点的坐标为,则这两个正方形位似中心的坐标是________.
?18.为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:根据光的反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离树的点处,然后观测考沿着直线后退到点,这时恰好在镜子里看到树梢顶点,再用皮尺量得,观测者目高,则树高约是________.(精确到)
?
19.已知在平面直角坐标系中,点、、,以原点为位似中心将缩小,位似比为,则点的对应点的坐标为________.
?20.点是的斜边上异于、的一点,过点作直线截,使截得的三角形与相似,请你在下图中画出满足条件的直线,并在相应的图形下面简要说明直线与的边的垂直或平行位置关系.
位置关系:________________________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )?
21.如图,在中,、分别为的三等分点,为上的中线,分别交、于、,求证:.
?
22.如图所示是一块形状为四边形的草地,周围均为水泥直道,两个拐角,处均为直角,草地中间另有一条水泥直道垂直于于点.若米,米,米,你能求出的长吗?
?
23.如图,中,,为上一个动点,过作,且与交于,与交于
若,,则________.(如图)
若,,求的值,写出求解过程.(如图)
若,,则________.(如图)
?
24.晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线移动,如图,当小军正好站在广场的点(距点块地砖长)时,其影长恰好为块地砖长;当小聪正好站在广场的点(距点块地砖长)时,其影长恰好为块地砖长.已知广场地面由边长为米的正方形地砖铺成,小聪的身高为米,,,,请你根据以上信息,求出小军身高的长(结果精确到米)
?
25.有一块三角形的余料,要把它加工成矩形的零件,已知,,高,矩形的边在边上,、分别在、上.
若,求的长;
问长为多少时,矩形的面积是三角形的面积的.
?
26.秋高气爽,菊花芬芳,艳阳高照,群情昂扬.某校八年级数学兴趣小组运用相似三角形的有关知识,并用两种方法测量学校操场南侧旗杆的高度.
如图①,小丽同学站在旗杆顶端在地面上的影子处,此时小丽同学头顶在地面上的影子处.若小丽同学身高,小丽同学的影长,旗杆的影长.利用得到的数据,请你帮助数学兴趣小组求出旗杆的高度;
如图②,小亮同学在旗杆与他之间的地面上平放一面小镜子,在镜子的处做上一个标记,,小亮同学看着镜子前后移动,直到看到旗杆顶端在镜子中的像与镜子上的标记重合,停止移动.此时小亮同学站在处,,眼睛观察镜子时距离地面的高度.利用得到的数据,请你帮助数学兴趣小组求出旗杆的高度.(友情提示:将两图中的人物看作垂直地面的线段,不用再画线作图)
答案
1.A
2.B
3.A
4.A
5.D
6.D
7.D
8.D
9.C
10.D
11.
12.
13.
14.
15.
16.
17.
18.
19.或
20.
21.解:如答图所示.
作已知图形的中心对称图形,以为对称中心.令,,.
∵,
∴:
∴,而:
∴,所以,.
∴.
22.解:如图,∵,于点,
∴,
∴,而,,,
∴(米).
23.解:∵,,
∴,,,四点共圆,
∵,,
∴,
∴,
∴;
过作的延长线于,,作的于,连,
先证,
得,
又,
即可得;过作的延长线于,
作的于,连,
先证,
得,
∴,
∴.
24.解:∵,,,
∴,
∴,,
∴,,
∴,
∴,
∴,
∴小军身高约为米.
25.解:∵,高,的长为、的长为,四边形是矩形,
∴,,,
∴,
∴,即.
∵,
∴,即;∵由可知,,
∴.
∵矩形的面积是三角形的面积的,
∴,即,解得,,
∴当长为或时,矩形的面积是三角形的面积的.
26.旗杆的高度是.?…在和中,
∵,,
∴.
∴.…
∴.
∴.
答:旗杆的高度是.…
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.若,则
A. B. C. D.
?2.已知是线段的黄金分割点,且,,则长约为( )
A. B. C. D.
?3.如图,两个位似图形和,若,则正确的是( )
A. B.
C. D.
?4.如果线段,,那么和的比例中项是( )
A. B. C. D.
?5.如图,中,交于点,交于点,如果,那么下列等式成立的是( )
A. B.
C. D.
?6.顶角为的等腰三角形称为黄金三角形,如图,五边形的条边相等,个内角相等,则图中共有黄金三角形的个数是( )
A. B. C. D.
?7.如图所示,顶角为的等腰三角形,其底边与腰之比等于,这样的三角形叫黄金三角形,已知腰长,为第一个黄金三角形,为第二个黄金三角形,为第三个黄金三角形,以此类推,第个黄金三角形的周长为( )
A. B.
C. D.
?8.如图,在平行四边形中,是上的一点,直线与的延长线交于点,并与交于点,下列式子中错误的是( )
A. B.
C. D.
?9.如图所示,在中,,若,,则的值为( )
A. B. C. D.
?10.如图,在正方形中,为对角线,为上一点,过点作,与、?分别交于点,,为的中点,连结、、、.下列结论:①;②;③;④若,则.其中结论正确的有( )
A.个 B.个 C.个 D.个
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,为线段上一点,与交于点,,交于点,交于点,则图中相似三角形有________对.
?12.在阳光下,高为的旗杆在地面上的影长为,在同一时刻,测得附近一座建筑物的影长为,则这座建筑物的高度为________.
?13.已知,,且的面积为,的面积为,则与周长之比为________.
?14.如图,在中,,于,,,则________.
?15.如图,已知中,,连接,的面积是面积的,则________.
?
16.在中,已知点、分别在边、上,如果,,,,,那么________.
?17.如图,正方形和正方形是位似形,点的坐标为,点的坐标为,则这两个正方形位似中心的坐标是________.
?18.为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:根据光的反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离树的点处,然后观测考沿着直线后退到点,这时恰好在镜子里看到树梢顶点,再用皮尺量得,观测者目高,则树高约是________.(精确到)
?
19.已知在平面直角坐标系中,点、、,以原点为位似中心将缩小,位似比为,则点的对应点的坐标为________.
?20.点是的斜边上异于、的一点,过点作直线截,使截得的三角形与相似,请你在下图中画出满足条件的直线,并在相应的图形下面简要说明直线与的边的垂直或平行位置关系.
位置关系:________________________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )?
21.如图,在中,、分别为的三等分点,为上的中线,分别交、于、,求证:.
?
22.如图所示是一块形状为四边形的草地,周围均为水泥直道,两个拐角,处均为直角,草地中间另有一条水泥直道垂直于于点.若米,米,米,你能求出的长吗?
?
23.如图,中,,为上一个动点,过作,且与交于,与交于
若,,则________.(如图)
若,,求的值,写出求解过程.(如图)
若,,则________.(如图)
?
24.晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线移动,如图,当小军正好站在广场的点(距点块地砖长)时,其影长恰好为块地砖长;当小聪正好站在广场的点(距点块地砖长)时,其影长恰好为块地砖长.已知广场地面由边长为米的正方形地砖铺成,小聪的身高为米,,,,请你根据以上信息,求出小军身高的长(结果精确到米)
?
25.有一块三角形的余料,要把它加工成矩形的零件,已知,,高,矩形的边在边上,、分别在、上.
若,求的长;
问长为多少时,矩形的面积是三角形的面积的.
?
26.秋高气爽,菊花芬芳,艳阳高照,群情昂扬.某校八年级数学兴趣小组运用相似三角形的有关知识,并用两种方法测量学校操场南侧旗杆的高度.
如图①,小丽同学站在旗杆顶端在地面上的影子处,此时小丽同学头顶在地面上的影子处.若小丽同学身高,小丽同学的影长,旗杆的影长.利用得到的数据,请你帮助数学兴趣小组求出旗杆的高度;
如图②,小亮同学在旗杆与他之间的地面上平放一面小镜子,在镜子的处做上一个标记,,小亮同学看着镜子前后移动,直到看到旗杆顶端在镜子中的像与镜子上的标记重合,停止移动.此时小亮同学站在处,,眼睛观察镜子时距离地面的高度.利用得到的数据,请你帮助数学兴趣小组求出旗杆的高度.(友情提示:将两图中的人物看作垂直地面的线段,不用再画线作图)
答案
1.A
2.B
3.A
4.A
5.D
6.D
7.D
8.D
9.C
10.D
11.
12.
13.
14.
15.
16.
17.
18.
19.或
20.
21.解:如答图所示.
作已知图形的中心对称图形,以为对称中心.令,,.
∵,
∴:
∴,而:
∴,所以,.
∴.
22.解:如图,∵,于点,
∴,
∴,而,,,
∴(米).
23.解:∵,,
∴,,,四点共圆,
∵,,
∴,
∴,
∴;
过作的延长线于,,作的于,连,
先证,
得,
又,
即可得;过作的延长线于,
作的于,连,
先证,
得,
∴,
∴.
24.解:∵,,,
∴,
∴,,
∴,,
∴,
∴,
∴,
∴小军身高约为米.
25.解:∵,高,的长为、的长为,四边形是矩形,
∴,,,
∴,
∴,即.
∵,
∴,即;∵由可知,,
∴.
∵矩形的面积是三角形的面积的,
∴,即,解得,,
∴当长为或时,矩形的面积是三角形的面积的.
26.旗杆的高度是.?…在和中,
∵,,
∴.
∴.…
∴.
∴.
答:旗杆的高度是.…
