10.1.3 画轴对称图形 同步练习(含解析)
文档属性
| 名称 | 10.1.3 画轴对称图形 同步练习(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 597.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-31 10:21:43 | ||
图片预览

文档简介
10.1 3.画轴对称图形
一、选择题
1.下列说法错误的是( )
A.成轴对称的两个图形一定在对称轴的同侧
B.轴对称图形的对应边相等,对应角相等
C.等腰三角形是轴对称图形
D.成轴对称的两个图形的对应点的连线被对称轴垂直平分
2.下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
图1
3.如图2,正六边形ABCDEF与正六边形A′B′C′(D′E′F′关于直线l对称下列判断错误的是( )
图2
A.AB=A′B′
B.BC∥B′C′
C.直线l⊥BB′
D.∠A′=120°
二、填空题
4.如图3,已知直线AB和△DEF,作△DEF关于直线AB的对称图形,将作图步骤补充完整:
(1)分别过点D,E,F作直线AB的垂线,垂足分别是__________;
(2)分别延长DM,EP,FN至________,使MG=______,PH=________,NI=________;
(3)顺次连结点______________,就得到△DEF关于直线AB的对称图形△GHI.
图3
三、解答题
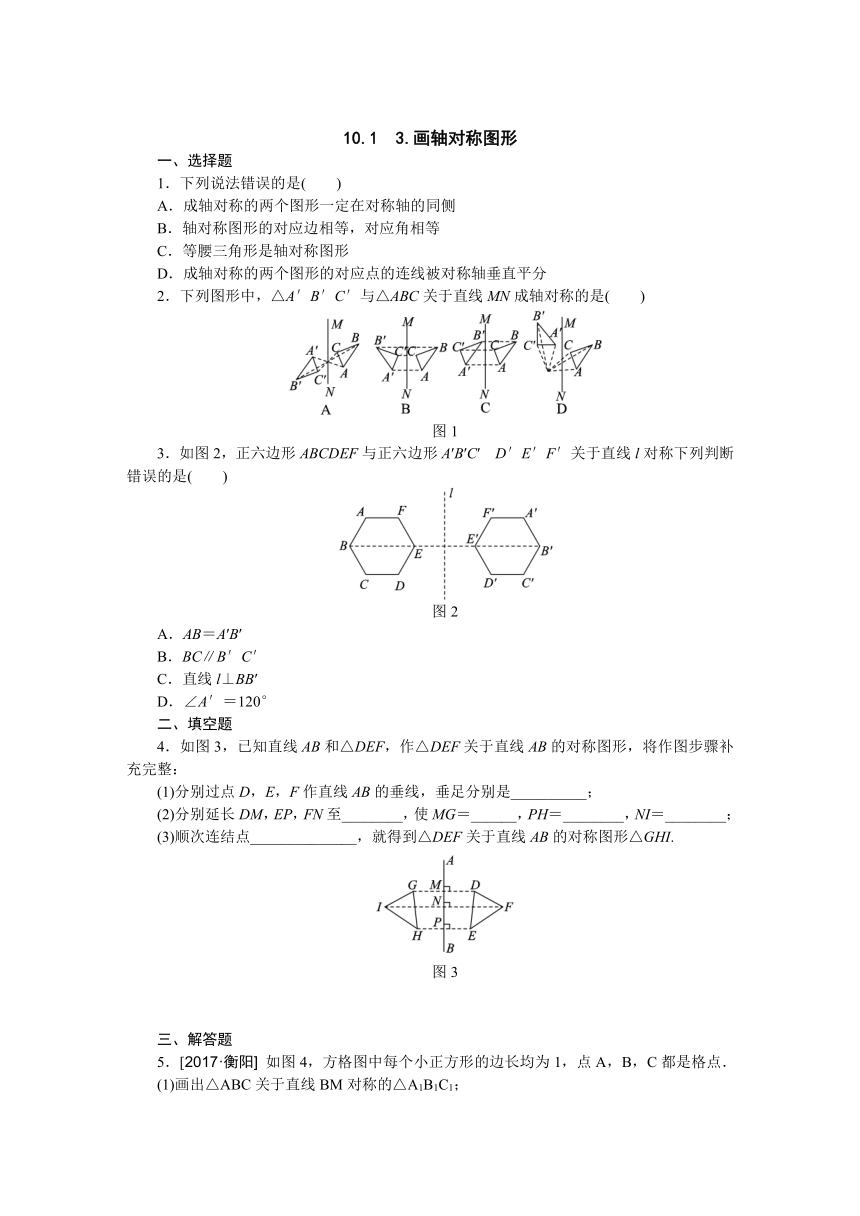
5.[2017·衡阳] 如图4,方格图中每个小正方形的边长均为1,点A,B,C都是格点.
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
图4
6、[实践探究] 在学习轴对称的时候,老师让同学们思考下面的问题.
如图5(1),要在燃气管道l上修建一个泵站,分别向A,B两镇供气.当泵站修在管道的什么地方时,可使所用的输气管道最短?
你可以在l上找几个点试一试,能发现什么规律?
图5
小华通过思考,很快得出了解决这个问题的正确办法.她把管道l看成一条直线(如图(2)),问题就转化为“要在直线l上找一点P,使AP与BP的和最小”.她的做法是这样的:
①作点B关于直线l的对称点B′;
②连结AB′交直线l于点P,则点P即为所求.
请你参考小华的做法解决下列问题:如图6,在△ABC中,D,E分别是AB,AC边的中点,请你在BC边上确定一点P,使△PDE的周长最小,在图中作出点P(保留作图痕迹,不写作法).
图6
1.[答案] A 2.[答案] B
3.[解析] B 关于某条直线对称的图形,对应线段不一定平行.
4.[答案] (1)M,P,N (2)点G,H,I DM EP
FN (3)G,H,I
5.解:(1)作图如下:
(2)由图直接读出AA1=10.
6 解:如图,作点D关于BC的对称点D′,连结D′E,与BC交于点P,则点P即为所求.
