16.3 可化为一元一次方程的分式方程课件共30张PPT)
文档属性
| 名称 | 16.3 可化为一元一次方程的分式方程课件共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 439.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-31 12:07:18 | ||
图片预览










文档简介
课件30张PPT。华东师大版八年级下册《数学》可化为
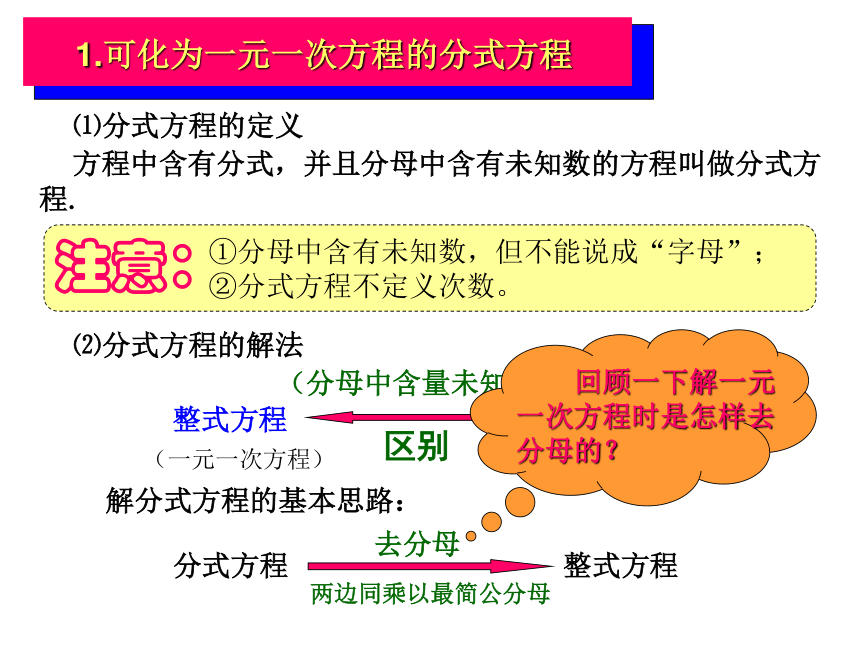
一元一次方程的分式方程一 、复习提问1、什么叫做方程?什么是一元一次方程?什么是方程的解?2、解一元一次方程的基本方法和步骤是什么?3、分式有意义的条件是什么?4、分式的基本性质是怎样的? 轮船在顺水中航行80千米所需的时间和逆水航行60千米所需的时间相同。已知水流的速度是3千米/时,求轮船在静水中的速度。设轮船在静水中的速度为x千米/时,根据题意,得 这个方程不是一元一次方程,它有什么特点?⑴含有分式;⑵分母中含有未知数。三、例题讲解与练习例2、下列方程哪些是分式方程:⑴分式方程的定义 方程中含有分式,并且分母中含有未知数的方程叫做分式方程.①分母中含有未知数,但不能说成“字母”;②分式方程不定义次数。⑵分式方程的解法 整式方程 分式方程
(一元一次方程)区别(分母中含量未知数)解分式方程的基本思路:分式方程 整式方程去分母两边同乘以最简公分母 回顾一下解一元一次方程时是怎样去分母的?1、思 考 :
怎样解分式方程呢?
请同学们先思考并回答以下问题:
1)、回顾一下一元一次方程时是怎么去分母的,从中能否得到一点启发?
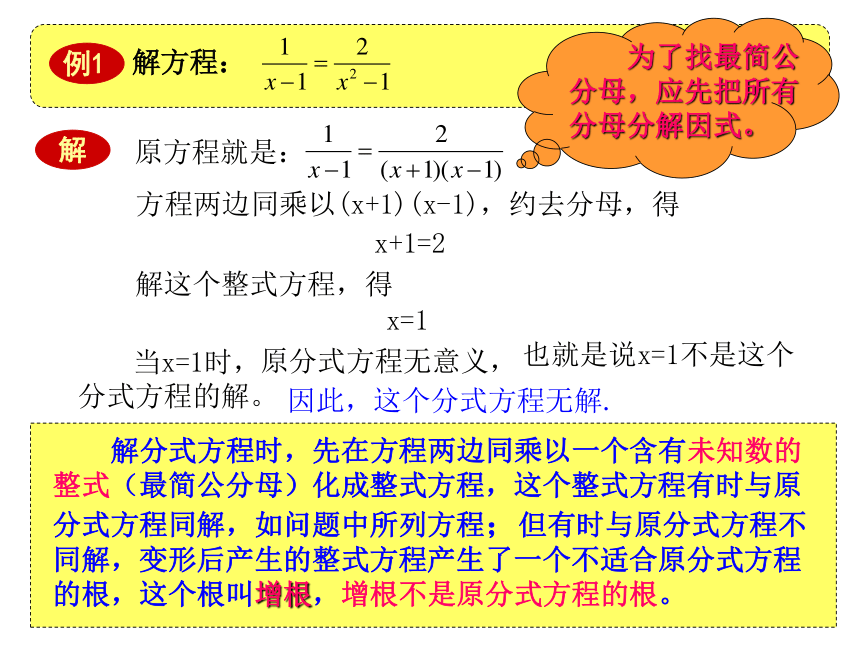
2)有没有办法可以去掉分式方程的分母把它转化为整式方程呢? 探究分式方程的解法 它们有区别吗?有联系吗?=去分母:等式基本性质2 通分:分式基本性质问题中所列方程 可以这样解:方程两边同乘以(x+3)(x-3),约去分母,得80(x-3)=60(x+3)解这个整式方程,得x=21当x=21时,∵左边=右边∴x=21是所列方程的解答:轮船在静水中的速度是21千米/时。 也就是说x=1不是这个分式方程的解。 解方程:原方程就是: 为了找最简公分母,应先把所有分母分解因式。方程两边同乘以(x+1)(x-1),约去分母,得x+1=2解这个整式方程,得x=1当x=1时,原分式方程无意义,因此,这个分式方程无解. 解分式方程时,先在方程两边同乘以一个含有未知数的整式(最简公分母)化成整式方程,这个整式方程有时与原分式方程同解,如问题中所列方程;但有时与原分式方程不同解,变形后产生的整式方程产生了一个不适合原分式方程的根,这个根叫增根,增根不是原分式方程的根。 由此可知,解分式方程可能产生增根。因此,解分式方程必须检验。为什么会产生增根呢? 我们知道对解方程变形时,必须根据方程的变形原理。如去分母时,只能在方程两边同乘以不等于零的数,所得的方程才与原方程同解,如一元一次方程。两边同乘以
(x+3)(x-3)(解为x=21)同解两边同乘以
(x+1)(x-1)≠0=0(解为x=1)不同解 检验时只须把整式方程的根代入最简公分母,看其值是否为0。 若最简公分母的值不为0,这个根就是分式方程的根,若最简公分母为0,则是增根。解分式方程的步骤:⑴去分母,将分式方程化为整式方程;⑵解整式方程(现在是一元一次方程);⑶检验;⑷写出原分式方程的根。 注意:去分母前应将分母分解因式,都按未知数的降幂排列。 解方程:原方程就是:方程两边同乘以x-3,约去分母,得x=2(x-3)+3解这个整式方程,得x=3检验:当x=3时,x-3=3-3=0,因此x=3是增根,舍去。∴原方程无解。注意:增根虽不是原分式方程的根,但它是整式方
程的根。(2)注意:解分式方程时可能产生增根,所以解分式方程一定要验根!例:解下列方程:练习:(1) 用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员每分钟各能输入多少个数据?分析: 本题是一个工作问题,其基本关系式是:工作总量=工作效率×工作时间 可以用表格的方式对这三个量进行分析,找出它们的等量关系。 设乙每分钟输入x个数据, 用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员每分钟各能输入多少个数据?解:即去分母并整理得120x=1320解得 x=11 经检验x=11是所列方程的根,答:甲每分钟各能输入22个数据,乙每分钟能输入11个数据。则甲每分钟输入2x个数据,根据题意,得:并且x=11时,2x=2×11=22,符合题意。 设自行车的速度是2x千米/时, 例 某校师生到距离学校20千米的公路旁植树,甲班师生骑自行车先走45分钟后,乙班师生乘校车出发,结果两班师生生同时达。已知自行车和校车的速度比是2∶5,求两种车的速度各是多少?解:即去分母并整理得3x=24解得 x=8 经检验x=8是所列方程的根,且符合题。答:自行车的速度是16千米/时,校车的速度是40千米/时。校车和速度是5x千米/时,根据题意,得:这时:2x=2×8=16千米/时,5x=5×8=40千米/时。列方程解应用题可以按以下步骤进行: ⑴弄清题意,特别是理清已知量和未知量之间的数量关系,设出未知数和列出有关代数式(写上单位); ⑵找到已知量和未知量之间的等量关系列出方程;⑶解所列方程;⑷检验;⑸作答(写上单位)。 检验应包括分式方程是否出现增根,也包括所解出的根是否符合应用题的题意。1、判断:3.下列关于分式方程增根的说法正确的是( )
A.使所有的分母的值都为零的解是增根;
B.分式方程的解为零就是增根
C.使分子的值为零的解就是增根;
D.使最简公分母的值为零的解是增根D A.方程两边分式的最简公分母是(x-1)(x+1)
B.方程两边都乘以(x-1)(x+1),得整式方程
2(x-1)+3(x+1)=6
C.解这个整式方程,得x=1
D.原方程的解为x=1D做一做1、解下列分式方程: 解方程:原方程就是:方程两边同乘以(x+1)(x-1),约去分母,得(x-3)(x-1)-(x+1)(x-1)=5整理得:-4x=1解得:检验: ∴原方程的解 。 解方程: 这时方程①不成立,m的值不存在将x=1代入方程①得: 若方程 有增根,求m的值。原方程就是:方程两边同乘以(x+1)(x-1),约去分母,得2(x-1)+m(x+1)=6 ①∵原方程的增根只可能是x=±12(1-1)+m(1+1)=6解得m=3将x=-1代入方程①得:2(-2-1)+m(-1+1)=6, 若方程 无解,求m的值。原方程就是:方程两边同乘以(x+1)(x-1),约去分母,得2(x-1)+m(x+1)=6 ①解这个方程得:当2+m=0,方程①无解,原分式方程也无解,这时m=-2;解分式方程的一般步骤是什么?分式方程整式方程x=aa不是分式
方程的解a是分式
方程的解最简公分母不为0最简公分母为0检验解整式方程去分母目标课堂小结同学们,再见!
一元一次方程的分式方程一 、复习提问1、什么叫做方程?什么是一元一次方程?什么是方程的解?2、解一元一次方程的基本方法和步骤是什么?3、分式有意义的条件是什么?4、分式的基本性质是怎样的? 轮船在顺水中航行80千米所需的时间和逆水航行60千米所需的时间相同。已知水流的速度是3千米/时,求轮船在静水中的速度。设轮船在静水中的速度为x千米/时,根据题意,得 这个方程不是一元一次方程,它有什么特点?⑴含有分式;⑵分母中含有未知数。三、例题讲解与练习例2、下列方程哪些是分式方程:⑴分式方程的定义 方程中含有分式,并且分母中含有未知数的方程叫做分式方程.①分母中含有未知数,但不能说成“字母”;②分式方程不定义次数。⑵分式方程的解法 整式方程 分式方程
(一元一次方程)区别(分母中含量未知数)解分式方程的基本思路:分式方程 整式方程去分母两边同乘以最简公分母 回顾一下解一元一次方程时是怎样去分母的?1、思 考 :
怎样解分式方程呢?
请同学们先思考并回答以下问题:
1)、回顾一下一元一次方程时是怎么去分母的,从中能否得到一点启发?
2)有没有办法可以去掉分式方程的分母把它转化为整式方程呢? 探究分式方程的解法 它们有区别吗?有联系吗?=去分母:等式基本性质2 通分:分式基本性质问题中所列方程 可以这样解:方程两边同乘以(x+3)(x-3),约去分母,得80(x-3)=60(x+3)解这个整式方程,得x=21当x=21时,∵左边=右边∴x=21是所列方程的解答:轮船在静水中的速度是21千米/时。 也就是说x=1不是这个分式方程的解。 解方程:原方程就是: 为了找最简公分母,应先把所有分母分解因式。方程两边同乘以(x+1)(x-1),约去分母,得x+1=2解这个整式方程,得x=1当x=1时,原分式方程无意义,因此,这个分式方程无解. 解分式方程时,先在方程两边同乘以一个含有未知数的整式(最简公分母)化成整式方程,这个整式方程有时与原分式方程同解,如问题中所列方程;但有时与原分式方程不同解,变形后产生的整式方程产生了一个不适合原分式方程的根,这个根叫增根,增根不是原分式方程的根。 由此可知,解分式方程可能产生增根。因此,解分式方程必须检验。为什么会产生增根呢? 我们知道对解方程变形时,必须根据方程的变形原理。如去分母时,只能在方程两边同乘以不等于零的数,所得的方程才与原方程同解,如一元一次方程。两边同乘以
(x+3)(x-3)(解为x=21)同解两边同乘以
(x+1)(x-1)≠0=0(解为x=1)不同解 检验时只须把整式方程的根代入最简公分母,看其值是否为0。 若最简公分母的值不为0,这个根就是分式方程的根,若最简公分母为0,则是增根。解分式方程的步骤:⑴去分母,将分式方程化为整式方程;⑵解整式方程(现在是一元一次方程);⑶检验;⑷写出原分式方程的根。 注意:去分母前应将分母分解因式,都按未知数的降幂排列。 解方程:原方程就是:方程两边同乘以x-3,约去分母,得x=2(x-3)+3解这个整式方程,得x=3检验:当x=3时,x-3=3-3=0,因此x=3是增根,舍去。∴原方程无解。注意:增根虽不是原分式方程的根,但它是整式方
程的根。(2)注意:解分式方程时可能产生增根,所以解分式方程一定要验根!例:解下列方程:练习:(1) 用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员每分钟各能输入多少个数据?分析: 本题是一个工作问题,其基本关系式是:工作总量=工作效率×工作时间 可以用表格的方式对这三个量进行分析,找出它们的等量关系。 设乙每分钟输入x个数据, 用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员每分钟各能输入多少个数据?解:即去分母并整理得120x=1320解得 x=11 经检验x=11是所列方程的根,答:甲每分钟各能输入22个数据,乙每分钟能输入11个数据。则甲每分钟输入2x个数据,根据题意,得:并且x=11时,2x=2×11=22,符合题意。 设自行车的速度是2x千米/时, 例 某校师生到距离学校20千米的公路旁植树,甲班师生骑自行车先走45分钟后,乙班师生乘校车出发,结果两班师生生同时达。已知自行车和校车的速度比是2∶5,求两种车的速度各是多少?解:即去分母并整理得3x=24解得 x=8 经检验x=8是所列方程的根,且符合题。答:自行车的速度是16千米/时,校车的速度是40千米/时。校车和速度是5x千米/时,根据题意,得:这时:2x=2×8=16千米/时,5x=5×8=40千米/时。列方程解应用题可以按以下步骤进行: ⑴弄清题意,特别是理清已知量和未知量之间的数量关系,设出未知数和列出有关代数式(写上单位); ⑵找到已知量和未知量之间的等量关系列出方程;⑶解所列方程;⑷检验;⑸作答(写上单位)。 检验应包括分式方程是否出现增根,也包括所解出的根是否符合应用题的题意。1、判断:3.下列关于分式方程增根的说法正确的是( )
A.使所有的分母的值都为零的解是增根;
B.分式方程的解为零就是增根
C.使分子的值为零的解就是增根;
D.使最简公分母的值为零的解是增根D A.方程两边分式的最简公分母是(x-1)(x+1)
B.方程两边都乘以(x-1)(x+1),得整式方程
2(x-1)+3(x+1)=6
C.解这个整式方程,得x=1
D.原方程的解为x=1D做一做1、解下列分式方程: 解方程:原方程就是:方程两边同乘以(x+1)(x-1),约去分母,得(x-3)(x-1)-(x+1)(x-1)=5整理得:-4x=1解得:检验: ∴原方程的解 。 解方程: 这时方程①不成立,m的值不存在将x=1代入方程①得: 若方程 有增根,求m的值。原方程就是:方程两边同乘以(x+1)(x-1),约去分母,得2(x-1)+m(x+1)=6 ①∵原方程的增根只可能是x=±12(1-1)+m(1+1)=6解得m=3将x=-1代入方程①得:2(-2-1)+m(-1+1)=6, 若方程 无解,求m的值。原方程就是:方程两边同乘以(x+1)(x-1),约去分母,得2(x-1)+m(x+1)=6 ①解这个方程得:当2+m=0,方程①无解,原分式方程也无解,这时m=-2;解分式方程的一般步骤是什么?分式方程整式方程x=aa不是分式
方程的解a是分式
方程的解最简公分母不为0最简公分母为0检验解整式方程去分母目标课堂小结同学们,再见!
