2020版高中数学新人教B版必修3课件:第二章统计章末复习(40张PPT)
文档属性
| 名称 | 2020版高中数学新人教B版必修3课件:第二章统计章末复习(40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-31 18:19:48 | ||
图片预览











文档简介
课件40张PPT。章末复习第二章 统 计学习目标
1.会根据不同的特点选择适当的抽样方法获得样本数据.
2.能利用图、表对样本数据进行整理分析,用样本和样本的数字特征估计总体.
3.能利用散点图对两个变量是否相关进行初步判断,能用回归直线方程进行预测.知识梳理达标检测题型探究内容索引知识梳理1.抽样方法
(1)用随机数表法抽样时,对个体所编号码位数要相同,当问题所给位数不同时,以位数较多的为准,在位数较少的数前面添“0”,凑齐位数.(3)三种抽样方法的异同点2.用样本估计总体
(1)用样本估计总体
用样本频率分布估计总体频率分布时,通常要对给定的一组数据作频率 与频率 .当样本只有两组数据且样本容量比较小时,用 刻画数据比较方便.
(2)样本的数字特征
样本的数字特征可分为两大类:一类是反映样本数据集中趋势的,包括 、 和 ;另一类是反映样本波动大小的,包括____及 .分布表分布直方图茎叶图众数中位数平均数方差标准差3.变量间的相关关系
(1)两个变量之间的相关关系的研究,通常先作变量的 ,根据散点图判断这两个变量最接近于哪种确定性关系(函数关系).
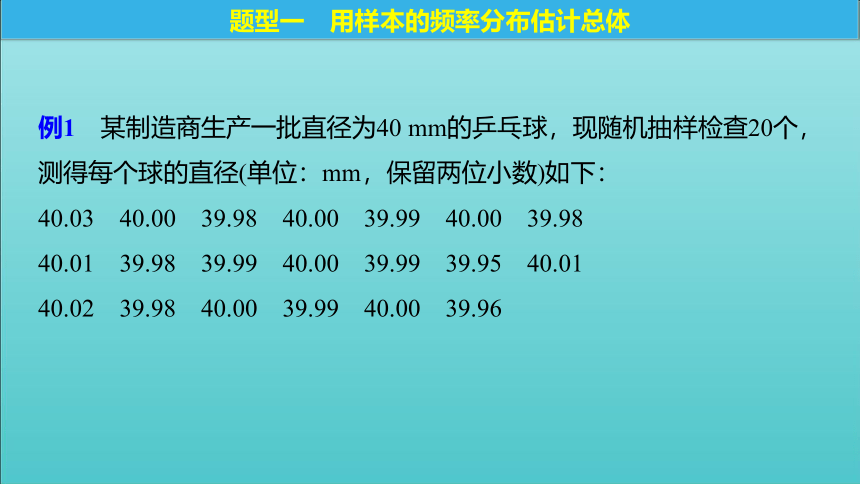
(2)求回归直线方程的步骤:散点图题型探究例1 某制造商生产一批直径为40 mm的乒乓球,现随机抽样检查20个,测得每个球的直径(单位:mm,保留两位小数)如下:
40.03 40.00 39.98 40.00 39.99 40.00 39.98
40.01 39.98 39.99 40.00 39.99 39.95 40.01
40.02 39.98 40.00 39.99 40.00 39.96题型一 用样本的频率分布估计总体解答(1)完成下面的频率分布表,并画出频率分布直方图;解 频率分布表如下:频率分布直方图如图:(2)假定乒乓球的直径误差不超过0.02 mm为合格品.若这批乒乓球的总数为10 000,试根据抽样检查结果估计这批产品的合格个数.解答解 ∵抽样的20个产品中在[39.98,40.02]范围内的有17个,∴10 000×85%=8 500.
故根据抽样检查结果,可以估计这批产品的合格个数为8 500.反思与感悟 总体分布中相应的统计图表主要包括:频率分布表、频率分布直方图、频率分布折线图等.通过这些统计图表给出的相应统计信息可以估计总体.解析 [4.7,4.8)之间频率为0.32,[4.6,4.7)之间频率为1-0.62-0.05-0.11=1-0.78=0.22,
∴a=(0.22+0.32)×100=54.跟踪训练1 为了了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,但知道后5组频数和为62,视力在4.6到4.8之间的学生数为a,最大频率为0.32,则a的值为
A.64 B.54 C.48 D.27 答案解析√题型二 用样本的数字特征估计总体的数字特征解答例2 某市共有50万户居民,城市调查队按千分之一的比例进行入户调查,抽样调查的结果如表:解答解答反思与感悟 样本的数字特征分为两大类:一类是反映样本数据集中趋势的特征数,例如平均数;另一类是反映样本数据波动大小的特征数,例如方差和标准差.通常我们用样本的平均数和方差(标准差)来近似代替总体的平均数和方差(标准差),从而实现对总体的估计.跟踪训练2 对甲、乙的学习成绩进行抽样分析,各抽5门功课,得到的观测数据如下:解答问:甲、乙谁的平均成绩好?谁的各门功课发展较平衡?所以甲的平均成绩好.题型三 用回归直线方程对总体进行估计例3 某车间为了制定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下:解答(1)在给定的坐标系中画出表中数据的散点图;解 散点图如图.解答解答(3)试预测加工10个零件需要多少小时?解 将x=10代入回归直线方程,故预测加工10个零件约需要8.05小时.反思与感悟 对两个变量进行研究,通常是先作出两个变量之间的散点图,根据散点图直观判断两个变量是否具有线性相关关系,如果具有,就可以应用最小二乘法求回归直线方程.由于样本可以反映总体,所以可以利用所求的回归直线方程,对这两个变量所确定的总体进行估计,即根据一个变量的取值,预测另一个变量的取值.跟踪训练3 理论预测某城市2020到2024年人口总数与年份的关系如下表所示:解答(1)请画出上表数据的散点图;解 数据的散点图如图:解答(2)指出x与y是否线性相关;解 由散点图可知,样本点基本上分布在一条直线附近,故x与y呈线性相关.解答解答故2025年该城市人口总数约为196万.(4)据此估计2025年该城市人口总数.
(参数数据:0×5+1×7+2×8+3×11+4×19=132,02+12+22+32+42=30)达标检测答案1.10个小球分别编有号码1,2,3,4,其中1号球4个,2号球2个,3号球3个,4号球1个,则数0.4是指1号球占总体分布的
A.频数 B.频率
C. D.以上都不对√12345答案解析2.现有10个数,其平均数是4,且这10个数的平方和是200,那么这组数的标准差是
A.1 B.2 C.3 D.4√解析 设这10个数为a1,a2,…,a10,且a1+a2+…+a10=40,12345解析 低于70分的频率为(0.012+0.018)×10=0.3,
所以不低于70分的频率为0.7,
故不低于70分的人数为50×0.7=35.3.某班50名学生的一次数学质量测验成绩的频率分布直方图如图所示,则成绩不低于70分的学生人数是_____.12345解析答案354.某农田施肥量x(单位:kg)与小麦产量y(单位:kg)之间的回归直线方程是 =4x+250,则当施肥量为50 kg时,可以预测小麦的产量为____kg.450答案解析12345123455.从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155 cm和195 cm之间,将测量结果按如下方式分成八组;第一组[155,160),第二组[160,165),…,第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组的人数相同,第六组的人数为4.
(1)求第七组的频率; 解答所以第七组的频率为1-0.08-5×(0.008×2+0.016+0.04×2+0.06)=0.06.12345(2)估计该校的800名男生的身高的中位数以及身高在180 cm以上(含180 cm)的人数.解答12345解 身高在第一组[155,160)的频率为0.008×5=0.04,
身高在第二组[160,165)的频率为0.016×5=0.08,
身高在第三组[165,170)的频率为0.04×5=0.2,
身高在第四组[170,175)的频率为0.04×5=0.2,
由于0.04+0.08+0.2=0.32<0.5,0.04+0.08+0.2+0.2=0.52>0.5,
估计这所学校的800名男生的身高的中位数为m,则170<m<175,
由0.04+0.08+0.2+(m-170)×0.04=0.5,得m=174.5,
所以可估计这所学校的800名男生的身高的中位数为174.5,
由直方图得后三组频率之和为0.06+0.08+0.008×5=0.18,
所以身高在180 cm以上(含180 cm)的人数为0.18×800=144.1.用频率分布直方图解决相关问题时,应正确理解图中各个量的意义,识图掌握信息是解决该类问题的关键.频率分布直方图有以下几个特点:
(1)纵轴表示频率/组距;(2)频率分布直方图中各小长方形高的比就是相应各组的频率之比;(3)直方图中各小长方形的面积是相应各组的频率,所有的小长方形的面积之和等于1,即频率之和为1.
2.平均数、中位数、众数与方差、标准差都是重要的数字特征,利用它们可对总体进行一种简明的描述,它们所反映的情况有着重要的实际意义,平均数、中位数、众数可描述总体的集中趋势,方差和标准差可描述波动大小.
1.会根据不同的特点选择适当的抽样方法获得样本数据.
2.能利用图、表对样本数据进行整理分析,用样本和样本的数字特征估计总体.
3.能利用散点图对两个变量是否相关进行初步判断,能用回归直线方程进行预测.知识梳理达标检测题型探究内容索引知识梳理1.抽样方法
(1)用随机数表法抽样时,对个体所编号码位数要相同,当问题所给位数不同时,以位数较多的为准,在位数较少的数前面添“0”,凑齐位数.(3)三种抽样方法的异同点2.用样本估计总体
(1)用样本估计总体
用样本频率分布估计总体频率分布时,通常要对给定的一组数据作频率 与频率 .当样本只有两组数据且样本容量比较小时,用 刻画数据比较方便.
(2)样本的数字特征
样本的数字特征可分为两大类:一类是反映样本数据集中趋势的,包括 、 和 ;另一类是反映样本波动大小的,包括____及 .分布表分布直方图茎叶图众数中位数平均数方差标准差3.变量间的相关关系
(1)两个变量之间的相关关系的研究,通常先作变量的 ,根据散点图判断这两个变量最接近于哪种确定性关系(函数关系).
(2)求回归直线方程的步骤:散点图题型探究例1 某制造商生产一批直径为40 mm的乒乓球,现随机抽样检查20个,测得每个球的直径(单位:mm,保留两位小数)如下:
40.03 40.00 39.98 40.00 39.99 40.00 39.98
40.01 39.98 39.99 40.00 39.99 39.95 40.01
40.02 39.98 40.00 39.99 40.00 39.96题型一 用样本的频率分布估计总体解答(1)完成下面的频率分布表,并画出频率分布直方图;解 频率分布表如下:频率分布直方图如图:(2)假定乒乓球的直径误差不超过0.02 mm为合格品.若这批乒乓球的总数为10 000,试根据抽样检查结果估计这批产品的合格个数.解答解 ∵抽样的20个产品中在[39.98,40.02]范围内的有17个,∴10 000×85%=8 500.
故根据抽样检查结果,可以估计这批产品的合格个数为8 500.反思与感悟 总体分布中相应的统计图表主要包括:频率分布表、频率分布直方图、频率分布折线图等.通过这些统计图表给出的相应统计信息可以估计总体.解析 [4.7,4.8)之间频率为0.32,[4.6,4.7)之间频率为1-0.62-0.05-0.11=1-0.78=0.22,
∴a=(0.22+0.32)×100=54.跟踪训练1 为了了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,但知道后5组频数和为62,视力在4.6到4.8之间的学生数为a,最大频率为0.32,则a的值为
A.64 B.54 C.48 D.27 答案解析√题型二 用样本的数字特征估计总体的数字特征解答例2 某市共有50万户居民,城市调查队按千分之一的比例进行入户调查,抽样调查的结果如表:解答解答反思与感悟 样本的数字特征分为两大类:一类是反映样本数据集中趋势的特征数,例如平均数;另一类是反映样本数据波动大小的特征数,例如方差和标准差.通常我们用样本的平均数和方差(标准差)来近似代替总体的平均数和方差(标准差),从而实现对总体的估计.跟踪训练2 对甲、乙的学习成绩进行抽样分析,各抽5门功课,得到的观测数据如下:解答问:甲、乙谁的平均成绩好?谁的各门功课发展较平衡?所以甲的平均成绩好.题型三 用回归直线方程对总体进行估计例3 某车间为了制定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下:解答(1)在给定的坐标系中画出表中数据的散点图;解 散点图如图.解答解答(3)试预测加工10个零件需要多少小时?解 将x=10代入回归直线方程,故预测加工10个零件约需要8.05小时.反思与感悟 对两个变量进行研究,通常是先作出两个变量之间的散点图,根据散点图直观判断两个变量是否具有线性相关关系,如果具有,就可以应用最小二乘法求回归直线方程.由于样本可以反映总体,所以可以利用所求的回归直线方程,对这两个变量所确定的总体进行估计,即根据一个变量的取值,预测另一个变量的取值.跟踪训练3 理论预测某城市2020到2024年人口总数与年份的关系如下表所示:解答(1)请画出上表数据的散点图;解 数据的散点图如图:解答(2)指出x与y是否线性相关;解 由散点图可知,样本点基本上分布在一条直线附近,故x与y呈线性相关.解答解答故2025年该城市人口总数约为196万.(4)据此估计2025年该城市人口总数.
(参数数据:0×5+1×7+2×8+3×11+4×19=132,02+12+22+32+42=30)达标检测答案1.10个小球分别编有号码1,2,3,4,其中1号球4个,2号球2个,3号球3个,4号球1个,则数0.4是指1号球占总体分布的
A.频数 B.频率
C. D.以上都不对√12345答案解析2.现有10个数,其平均数是4,且这10个数的平方和是200,那么这组数的标准差是
A.1 B.2 C.3 D.4√解析 设这10个数为a1,a2,…,a10,且a1+a2+…+a10=40,12345解析 低于70分的频率为(0.012+0.018)×10=0.3,
所以不低于70分的频率为0.7,
故不低于70分的人数为50×0.7=35.3.某班50名学生的一次数学质量测验成绩的频率分布直方图如图所示,则成绩不低于70分的学生人数是_____.12345解析答案354.某农田施肥量x(单位:kg)与小麦产量y(单位:kg)之间的回归直线方程是 =4x+250,则当施肥量为50 kg时,可以预测小麦的产量为____kg.450答案解析12345123455.从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155 cm和195 cm之间,将测量结果按如下方式分成八组;第一组[155,160),第二组[160,165),…,第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组的人数相同,第六组的人数为4.
(1)求第七组的频率; 解答所以第七组的频率为1-0.08-5×(0.008×2+0.016+0.04×2+0.06)=0.06.12345(2)估计该校的800名男生的身高的中位数以及身高在180 cm以上(含180 cm)的人数.解答12345解 身高在第一组[155,160)的频率为0.008×5=0.04,
身高在第二组[160,165)的频率为0.016×5=0.08,
身高在第三组[165,170)的频率为0.04×5=0.2,
身高在第四组[170,175)的频率为0.04×5=0.2,
由于0.04+0.08+0.2=0.32<0.5,0.04+0.08+0.2+0.2=0.52>0.5,
估计这所学校的800名男生的身高的中位数为m,则170<m<175,
由0.04+0.08+0.2+(m-170)×0.04=0.5,得m=174.5,
所以可估计这所学校的800名男生的身高的中位数为174.5,
由直方图得后三组频率之和为0.06+0.08+0.008×5=0.18,
所以身高在180 cm以上(含180 cm)的人数为0.18×800=144.1.用频率分布直方图解决相关问题时,应正确理解图中各个量的意义,识图掌握信息是解决该类问题的关键.频率分布直方图有以下几个特点:
(1)纵轴表示频率/组距;(2)频率分布直方图中各小长方形高的比就是相应各组的频率之比;(3)直方图中各小长方形的面积是相应各组的频率,所有的小长方形的面积之和等于1,即频率之和为1.
2.平均数、中位数、众数与方差、标准差都是重要的数字特征,利用它们可对总体进行一种简明的描述,它们所反映的情况有着重要的实际意义,平均数、中位数、众数可描述总体的集中趋势,方差和标准差可描述波动大小.
