2020版高中数学新人教B版必修3课件:第三章概率章末复习(42张PPT)
文档属性
| 名称 | 2020版高中数学新人教B版必修3课件:第三章概率章末复习(42张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-31 00:00:00 | ||
图片预览











文档简介
课件42张PPT。章末复习第三章 概 率学习目标
1.理解频率与概率的关系,会用随机模拟的方法用频率估计概率.
2.掌握随机事件的概率及其基本性质,能把较复杂的事件转化为较简单的互斥事件求概率.
3.能区分古典概型与几何概型,并能求相应概率.知识梳理达标检测题型探究内容索引知识梳理1.频率与概率
频率是概率的 ,是随机的,随着试验的不同而 ;概率是多数次的试验中 的稳定值,是一个 ,不要用一次或少数次试验中的频率来估计概率.
2.求较复杂概率的常用方法
(1)将所求事件转化为彼此 的事件的和;
(2)先求其 事件的概率,然后再应用公式P(A)=1-P( )求解.近似值变化频率常数互斥对立3.古典概型概率的计算:关键要分清基本事件的总数n与事件A包含的基本事件的个数m,再利用公式P(A)= 求解.有时需要用列举法把基本事件一一列举出来,在列举时必须按某一顺序做到不重不漏.
4.几何概型事件概率的计算
关键是求得事件A所占 和 的几何测度,然后代入公式求解.区域整个区域[思考辨析 判断正误]
1.对立事件一定是互斥事件,互斥事件不一定是对立事件.( )
2.“在适当条件下,种下一粒种子观察它是否发芽”属于古典概型.( )
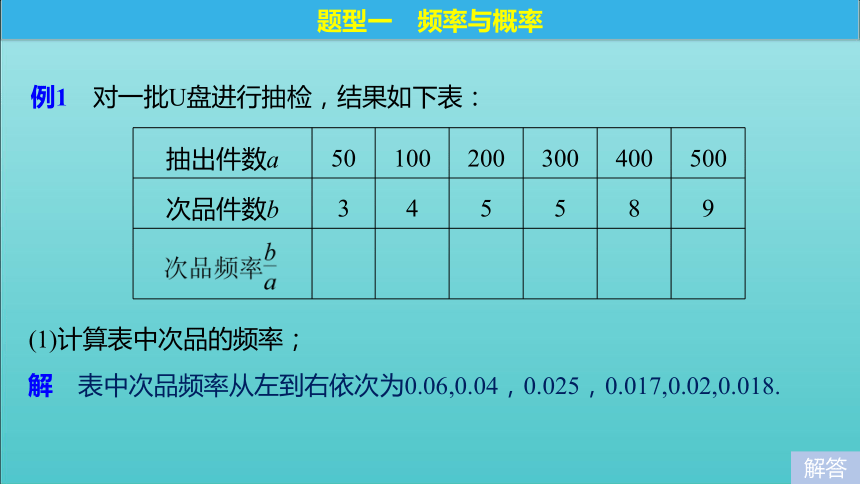
3.几何概型中,每一个基本事件就是从某个特定的几何区域内随机地取一点,该区域中的每一点被取到的机会相等.( )√×√题型探究例1 对一批U盘进行抽检,结果如下表:题型一 频率与概率(1)计算表中次品的频率;解答解 表中次品频率从左到右依次为0.06,0.04,0.025,0.017,0.02,0.018.(2)从这批U盘中任意抽取一个是次品的概率约是多少?
(3)为保证买到次品的顾客能够及时更换,要销售2 000个U盘,至少需进货多少个U盘?解答解 当抽取件数a越来越大时,出现次品的频率在0.02附近摆动,所以从这批U盘中任意抽取一个是次品的概率约是0.02.
解 设需要进货x个U盘,为保证其中有2 000个正品U盘,则x(1-0.02)≥2 000,因为x是正整数,所以x≥2 041,即至少需进货2 041个U盘.反思与感悟 概率是个常数.但除了几何概型,概率并不易知,故可用频率来估计.跟踪训练1 某射击运动员为备战奥运会,在相同条件下进行射击训练,结果如下:(1)该射击运动员射击一次,击中靶心的概率大约是多少?
(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少?解答解 由题意得,击中靶心的频率与0.9接近,故概率约为0.9.
解 击中靶心的次数大约为300×0.9=270.(3)假如该射击运动员射击了300次,前270次都击中靶心,那么后30次一定都击不中靶心吗?
(4)假如该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗?解答解 由概率的意义,可知概率是个常数,不因试验次数的变化而变化.后30次中,每次击中靶心的概率仍是0.9,所以不一定不击中靶心.
解 不一定.题型二 互斥事件与对立事件解答例2 甲、乙两人参加普法知识竞赛,共有5个不同题目,选择题3个,判断题2个,甲、乙两人各抽一题.
(1)甲、乙两人中有一个抽到选择题,另一个抽到判断题的概率是多少?解 把3个选择题记为x1,x2,x3,2个判断题记为p1,p2.“甲抽到选择题,乙抽到判断题”的情况有:(x1,p1),(x1,p2),(x2,p1),(x2,p2),(x3,p1),(x3,p2),共6种;
“甲抽到判断题,乙抽到选择题”的情况有:(p1,x1),(p1,x2),(p1,x3),(p2,x1),(p2,x2),(p2,x3),共6种;
“甲、乙都抽到选择题”的情况有:(x1,x2),(x1,x3),(x2,x1),(x2,x3),(x3,x1),(x3,x2),共6种;“甲、乙都抽到判断题”的情况有:(p1,p2),(p2,p1),共2种.
因此基本事件的总数为6+6+6+2=20.故“甲、乙两人中有一个抽到选择题,解答(2)甲、乙两人中至少有一人抽到选择题的概率是多少?反思与感悟 在求有关事件的概率时,若从正面分析,包含的事件较多或较烦琐,而其反面却较容易入手,这时,可以利用对立事件求解.解答跟踪训练2 猎人在距离100米处射击一野兔,命中的概率为 ,如果第一次没有命中,则猎人进行第二次射击,但距离已是150米,如果又没有击中,则猎人进行第三次射击,但距离已是200米.已知猎人命中兔子的概率与距离的平方成反比,则三次内击中野兔的概率是多少?解 三次内击中野兔,即第一次击中野兔或第二次击中野兔或第三次击中野兔,
设第一、二、三次击中野兔分别为事件A,B,C.所以P(A∪B∪C)=P(A)+P(B)+P(C)题型三 古典概型与几何概型例3 某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:解答(1)利用上表提供的样本数据估计该批产品的一等品率;解 计算10件产品的综合指标S,如下表:其中S≤4的有A1,A2,A4,A5,A7,A9,共6件,从而可估计该批产品的一等品率为0.6.解答(2)在该样本的一等品中,随机抽取2件产品,
①用产品编号列出所有可能的结果;解 在该样本的一等品中,随机抽取2件产品的所有可能结果为{A1,A2},{A1,A4},{A1,A5},{A1,A7},{A1,A9},{A2,A4},{A2,A5},{A2,A7},{A2,A9},{A4,A5},{A4,A7},{A4,A9},{A5,A7},{A5,A9},{A7,A9},共15种.解答②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.解 在该样本的一等品中,综合指标S等于4的产品编号分别为A1,A2,A5,A7,
则事件B发生的所有可能结果为{A1,A2},{A1,A5},{A1,A7},{A2,A5},{A2,A7},{A5,A7},共6种.反思与感悟 古典概型与几何概型的共同点是各基本事件的等可能性;不同点是前者总的基本事件有限,后者无限.跟踪训练3 如图所示的大正方形面积为13,四个全等的直角三角形围成一个阴影小正方形,较短的直角边边长为2,向大正方形内投掷飞镖,则飞镖落在阴影部分的概率为 答案解析√解析 设阴影小正方形边长为x,则在直角三角形中有22+(x+2)2= 解得x=1或x=-5(舍去),
∴阴影部分面积为1,题型四 数形结合思想在求解概率中的应用解答例4 口袋里装有2个白球和2个黑球,这4个球除颜色外完全相同,四个人按顺序依次从中摸出1个球(不放回),试求“第二个人摸到白球”的概率.解 把四个人依次编号为甲、乙、丙、丁,把2个白球编上序号1,2,把2个黑球也编上序号1,2,于是四个人按顺序依次从袋内摸出1个球的所有可能结果,可用树形图直观地表示出来,如图所示.
从右面的树形图可以看出,试验的所有可能结果为24.第二人摸到白球的结果有12种,记第二个人摸到白球为事件A, 反思与感悟 事件个数没有很明显的规律,而且涉及的基本事件又不是太多时,我们可借助树形图直观地将其表示出来,有利于条理地思考和表达.跟踪训练4 如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部分的概率是 答案解析√解析 设分别以OA,OB为直径的两个半圆交于点C,OA的中点为D,如图,连接OC,DC.
不妨令OA=OB=2,
则OD=DA=DC=1.所以整体图形中空白部分面积S2=2.所以阴影部分面积为S3=π-2.达标检测答案解析1.下列事件:
①任取三条线段,这三条线段恰好组成直角三角形;②从一个三角形的三个顶点各任画一条射线,这三条射线交于一点;③实数a,b都不为0,但a2+b2=0;④明年12月28日的最高气温高于今年12月28日的最高气温,其中为随机事件的是
A.①②③ B.①②④
C.①③④ D.②③④√1234512345解析 任取三条线段,这三条线段可能组成直角三角形,也可能组不成直角三角形,故①为随机事件;
从一个三角形的三个顶点各任画一条射线,三条射线可能不相交,交于一点、交于两点、交于三点,故②为随机事件;
若实数a,b都不为0,则a2+b2一定不等于0,故③为不可能事件;
由于明年12月28日还未到来,故明年12月28日的最高气温可能高于今年12月28日的最高气温,
也可能低于今年12月28日的最高气温,
还可能等于今年12月28日的最高气温.故④为随机事件.故选B.答案解析2.把黑、红、白3张纸牌分给甲、乙、丙三人,则事件“甲分得红牌”与“乙分得红牌”是
A.对立事件 B.互斥但不对立事件
C.不可能事件 D.必然事件√12345解析 根据题意,把黑、红、白3张纸牌分给甲、乙、丙三人,事件“甲分得红牌”与“乙分得红牌”不会同时发生,
故两者是互斥事件,但除了“甲分得红牌”与“乙分得红牌”之外,还有“丙分得红牌”,故两者不是对立事件,
所以事件“甲分得红牌”与“乙分得红牌”是互斥但不对立事件.3.下列试验属于古典概型的有
①从装有大小、形状完全相同的红、黑、绿各一球的袋子中任意取出一球,观察球的颜色;②在公交车站候车不超过10分钟的概率;③同时抛掷两枚硬币,观察出现“两正”“两反”“一正一反”的次数;④从一桶水中取出100 mL,观察是否含有大肠杆菌.
A.1个 B.2个 C.3个 D.4个12345解析答案√解析 古典概型的两个基本特征是有限性和等可能性.①符合两个特征;
对于②和④,基本事件的个数有无限多个;
对于③,出现“两正”“两反”与“一正一反”的可能性并不相等,故选A.4.甲、乙两人随意入住两间空房,则甲、乙两人各住一间房的概率是 解析12345答案√解析 共有4个事件“甲、乙同住房间A,甲、乙同住房间B,甲住A乙住B,甲住B乙住A”,
且各事件等可能,两人各住一个房间共有两种情况,5.任取一个三位正整数N,则对数log2N是一个正整数的概率是 解析 三位正整数有100~999,共900个,而满足log2N为正整数的N有27,28,29,共3个,12345解析答案√1.两个事件互斥,它们未必对立;反之,两个事件对立,它们一定互斥.若事件A1,A2,A3,…,An彼此互斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
2.关于古典概型,必须要解决好下面三个方面的问题:
(1)本试验是不是等可能的?
(2)本试验的基本事件有多少个?
(3)事件A是什么,它包含多少个基本事件?
只有回答好这三个方面的问题,解题才不会出错.3.几何概型的试验中,事件A的概率P(A)只与子区域A的几何度量(长度、面积或体积)成正比,而与A的位置和形状无关.求试验为几何概型的概率,关键是求得事件所占区域和整个区域Ω的几何度量,然后代入公式即可求解.
1.理解频率与概率的关系,会用随机模拟的方法用频率估计概率.
2.掌握随机事件的概率及其基本性质,能把较复杂的事件转化为较简单的互斥事件求概率.
3.能区分古典概型与几何概型,并能求相应概率.知识梳理达标检测题型探究内容索引知识梳理1.频率与概率
频率是概率的 ,是随机的,随着试验的不同而 ;概率是多数次的试验中 的稳定值,是一个 ,不要用一次或少数次试验中的频率来估计概率.
2.求较复杂概率的常用方法
(1)将所求事件转化为彼此 的事件的和;
(2)先求其 事件的概率,然后再应用公式P(A)=1-P( )求解.近似值变化频率常数互斥对立3.古典概型概率的计算:关键要分清基本事件的总数n与事件A包含的基本事件的个数m,再利用公式P(A)= 求解.有时需要用列举法把基本事件一一列举出来,在列举时必须按某一顺序做到不重不漏.
4.几何概型事件概率的计算
关键是求得事件A所占 和 的几何测度,然后代入公式求解.区域整个区域[思考辨析 判断正误]
1.对立事件一定是互斥事件,互斥事件不一定是对立事件.( )
2.“在适当条件下,种下一粒种子观察它是否发芽”属于古典概型.( )
3.几何概型中,每一个基本事件就是从某个特定的几何区域内随机地取一点,该区域中的每一点被取到的机会相等.( )√×√题型探究例1 对一批U盘进行抽检,结果如下表:题型一 频率与概率(1)计算表中次品的频率;解答解 表中次品频率从左到右依次为0.06,0.04,0.025,0.017,0.02,0.018.(2)从这批U盘中任意抽取一个是次品的概率约是多少?
(3)为保证买到次品的顾客能够及时更换,要销售2 000个U盘,至少需进货多少个U盘?解答解 当抽取件数a越来越大时,出现次品的频率在0.02附近摆动,所以从这批U盘中任意抽取一个是次品的概率约是0.02.
解 设需要进货x个U盘,为保证其中有2 000个正品U盘,则x(1-0.02)≥2 000,因为x是正整数,所以x≥2 041,即至少需进货2 041个U盘.反思与感悟 概率是个常数.但除了几何概型,概率并不易知,故可用频率来估计.跟踪训练1 某射击运动员为备战奥运会,在相同条件下进行射击训练,结果如下:(1)该射击运动员射击一次,击中靶心的概率大约是多少?
(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少?解答解 由题意得,击中靶心的频率与0.9接近,故概率约为0.9.
解 击中靶心的次数大约为300×0.9=270.(3)假如该射击运动员射击了300次,前270次都击中靶心,那么后30次一定都击不中靶心吗?
(4)假如该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗?解答解 由概率的意义,可知概率是个常数,不因试验次数的变化而变化.后30次中,每次击中靶心的概率仍是0.9,所以不一定不击中靶心.
解 不一定.题型二 互斥事件与对立事件解答例2 甲、乙两人参加普法知识竞赛,共有5个不同题目,选择题3个,判断题2个,甲、乙两人各抽一题.
(1)甲、乙两人中有一个抽到选择题,另一个抽到判断题的概率是多少?解 把3个选择题记为x1,x2,x3,2个判断题记为p1,p2.“甲抽到选择题,乙抽到判断题”的情况有:(x1,p1),(x1,p2),(x2,p1),(x2,p2),(x3,p1),(x3,p2),共6种;
“甲抽到判断题,乙抽到选择题”的情况有:(p1,x1),(p1,x2),(p1,x3),(p2,x1),(p2,x2),(p2,x3),共6种;
“甲、乙都抽到选择题”的情况有:(x1,x2),(x1,x3),(x2,x1),(x2,x3),(x3,x1),(x3,x2),共6种;“甲、乙都抽到判断题”的情况有:(p1,p2),(p2,p1),共2种.
因此基本事件的总数为6+6+6+2=20.故“甲、乙两人中有一个抽到选择题,解答(2)甲、乙两人中至少有一人抽到选择题的概率是多少?反思与感悟 在求有关事件的概率时,若从正面分析,包含的事件较多或较烦琐,而其反面却较容易入手,这时,可以利用对立事件求解.解答跟踪训练2 猎人在距离100米处射击一野兔,命中的概率为 ,如果第一次没有命中,则猎人进行第二次射击,但距离已是150米,如果又没有击中,则猎人进行第三次射击,但距离已是200米.已知猎人命中兔子的概率与距离的平方成反比,则三次内击中野兔的概率是多少?解 三次内击中野兔,即第一次击中野兔或第二次击中野兔或第三次击中野兔,
设第一、二、三次击中野兔分别为事件A,B,C.所以P(A∪B∪C)=P(A)+P(B)+P(C)题型三 古典概型与几何概型例3 某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:解答(1)利用上表提供的样本数据估计该批产品的一等品率;解 计算10件产品的综合指标S,如下表:其中S≤4的有A1,A2,A4,A5,A7,A9,共6件,从而可估计该批产品的一等品率为0.6.解答(2)在该样本的一等品中,随机抽取2件产品,
①用产品编号列出所有可能的结果;解 在该样本的一等品中,随机抽取2件产品的所有可能结果为{A1,A2},{A1,A4},{A1,A5},{A1,A7},{A1,A9},{A2,A4},{A2,A5},{A2,A7},{A2,A9},{A4,A5},{A4,A7},{A4,A9},{A5,A7},{A5,A9},{A7,A9},共15种.解答②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.解 在该样本的一等品中,综合指标S等于4的产品编号分别为A1,A2,A5,A7,
则事件B发生的所有可能结果为{A1,A2},{A1,A5},{A1,A7},{A2,A5},{A2,A7},{A5,A7},共6种.反思与感悟 古典概型与几何概型的共同点是各基本事件的等可能性;不同点是前者总的基本事件有限,后者无限.跟踪训练3 如图所示的大正方形面积为13,四个全等的直角三角形围成一个阴影小正方形,较短的直角边边长为2,向大正方形内投掷飞镖,则飞镖落在阴影部分的概率为 答案解析√解析 设阴影小正方形边长为x,则在直角三角形中有22+(x+2)2= 解得x=1或x=-5(舍去),
∴阴影部分面积为1,题型四 数形结合思想在求解概率中的应用解答例4 口袋里装有2个白球和2个黑球,这4个球除颜色外完全相同,四个人按顺序依次从中摸出1个球(不放回),试求“第二个人摸到白球”的概率.解 把四个人依次编号为甲、乙、丙、丁,把2个白球编上序号1,2,把2个黑球也编上序号1,2,于是四个人按顺序依次从袋内摸出1个球的所有可能结果,可用树形图直观地表示出来,如图所示.
从右面的树形图可以看出,试验的所有可能结果为24.第二人摸到白球的结果有12种,记第二个人摸到白球为事件A, 反思与感悟 事件个数没有很明显的规律,而且涉及的基本事件又不是太多时,我们可借助树形图直观地将其表示出来,有利于条理地思考和表达.跟踪训练4 如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部分的概率是 答案解析√解析 设分别以OA,OB为直径的两个半圆交于点C,OA的中点为D,如图,连接OC,DC.
不妨令OA=OB=2,
则OD=DA=DC=1.所以整体图形中空白部分面积S2=2.所以阴影部分面积为S3=π-2.达标检测答案解析1.下列事件:
①任取三条线段,这三条线段恰好组成直角三角形;②从一个三角形的三个顶点各任画一条射线,这三条射线交于一点;③实数a,b都不为0,但a2+b2=0;④明年12月28日的最高气温高于今年12月28日的最高气温,其中为随机事件的是
A.①②③ B.①②④
C.①③④ D.②③④√1234512345解析 任取三条线段,这三条线段可能组成直角三角形,也可能组不成直角三角形,故①为随机事件;
从一个三角形的三个顶点各任画一条射线,三条射线可能不相交,交于一点、交于两点、交于三点,故②为随机事件;
若实数a,b都不为0,则a2+b2一定不等于0,故③为不可能事件;
由于明年12月28日还未到来,故明年12月28日的最高气温可能高于今年12月28日的最高气温,
也可能低于今年12月28日的最高气温,
还可能等于今年12月28日的最高气温.故④为随机事件.故选B.答案解析2.把黑、红、白3张纸牌分给甲、乙、丙三人,则事件“甲分得红牌”与“乙分得红牌”是
A.对立事件 B.互斥但不对立事件
C.不可能事件 D.必然事件√12345解析 根据题意,把黑、红、白3张纸牌分给甲、乙、丙三人,事件“甲分得红牌”与“乙分得红牌”不会同时发生,
故两者是互斥事件,但除了“甲分得红牌”与“乙分得红牌”之外,还有“丙分得红牌”,故两者不是对立事件,
所以事件“甲分得红牌”与“乙分得红牌”是互斥但不对立事件.3.下列试验属于古典概型的有
①从装有大小、形状完全相同的红、黑、绿各一球的袋子中任意取出一球,观察球的颜色;②在公交车站候车不超过10分钟的概率;③同时抛掷两枚硬币,观察出现“两正”“两反”“一正一反”的次数;④从一桶水中取出100 mL,观察是否含有大肠杆菌.
A.1个 B.2个 C.3个 D.4个12345解析答案√解析 古典概型的两个基本特征是有限性和等可能性.①符合两个特征;
对于②和④,基本事件的个数有无限多个;
对于③,出现“两正”“两反”与“一正一反”的可能性并不相等,故选A.4.甲、乙两人随意入住两间空房,则甲、乙两人各住一间房的概率是 解析12345答案√解析 共有4个事件“甲、乙同住房间A,甲、乙同住房间B,甲住A乙住B,甲住B乙住A”,
且各事件等可能,两人各住一个房间共有两种情况,5.任取一个三位正整数N,则对数log2N是一个正整数的概率是 解析 三位正整数有100~999,共900个,而满足log2N为正整数的N有27,28,29,共3个,12345解析答案√1.两个事件互斥,它们未必对立;反之,两个事件对立,它们一定互斥.若事件A1,A2,A3,…,An彼此互斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
2.关于古典概型,必须要解决好下面三个方面的问题:
(1)本试验是不是等可能的?
(2)本试验的基本事件有多少个?
(3)事件A是什么,它包含多少个基本事件?
只有回答好这三个方面的问题,解题才不会出错.3.几何概型的试验中,事件A的概率P(A)只与子区域A的几何度量(长度、面积或体积)成正比,而与A的位置和形状无关.求试验为几何概型的概率,关键是求得事件所占区域和整个区域Ω的几何度量,然后代入公式即可求解.
