17.2.2 函数的图象 课件(19张PPT)
文档属性
| 名称 | 17.2.2 函数的图象 课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 809.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-31 16:41:26 | ||
图片预览





文档简介
课件19张PPT。第17章 函数及其图象
17.2函数的图象
2.函数的图象
气温曲线是用图象表示函数的一个实际例子,那么什么是函数图象?
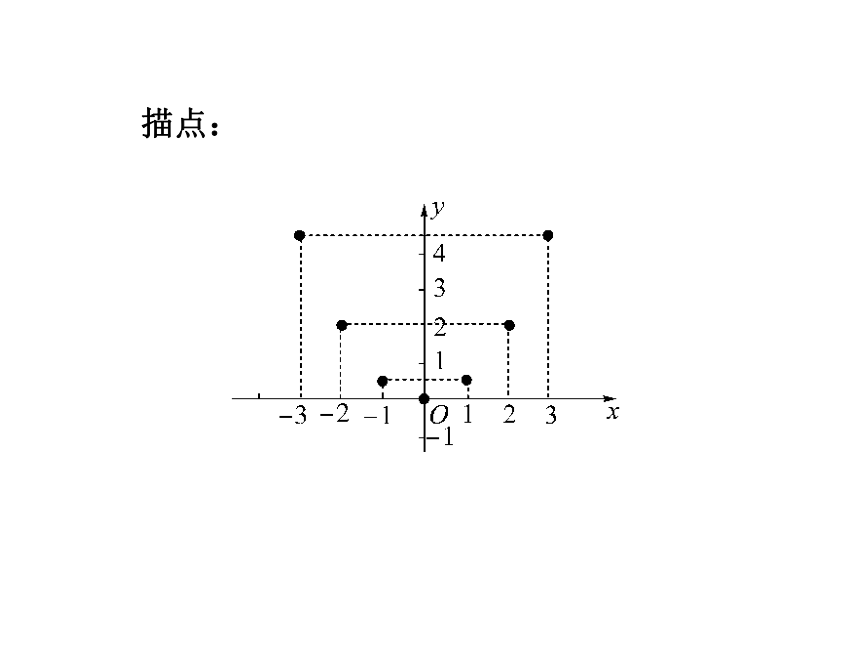
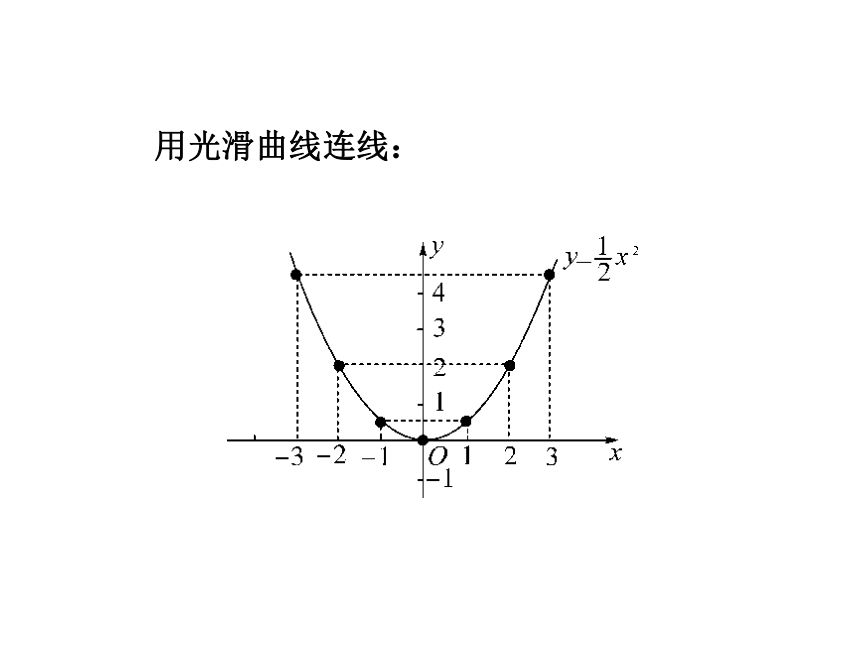
你能利用函数解析式画出一些函数的图象吗?探究1:画函数图象画出函数y= 的图象描点:用光滑曲线连线:【归纳结论】画函数图象的方法,可以概括为列表、描点、连线三步,通常称为描点法.探究2:利用函数图象解决实际问题
王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上山,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分)之间的S函数关系(从小强开始爬山时计时).看图回答问题.1.小强让爷爷先上多少米?
2.山顶离山脚的距离有多少米?谁先爬上山顶?
3.小强通过多少时间追上爷爷?【分析】
在观察实际问题的图象时,先从两坐标轴表示的实际意义得到点的坐标意义.再从图形中分析两变量的相互关系,寻找对应的现实情境.如图中的两条线段都可以看出随着自变量x的逐渐增大,函数值y也随着逐渐增大,再联系现实情境爬山所用时间越长,离开山脚的距离越大,当x达到最大值时,也就是到达山顶.
解:1.60米 2.300米 小强 3.8分1.画出函数y=x+1的图象
解:列表描点:连线:2.小明从家里出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家.下面的图描述了小明在散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.
请你由图具体说明小明散步的情况.解:小明先走了约3分钟,到达离家250米处的一个阅报栏前看了5分钟报,又向前走了2分钟,到达离家450米处返回,走了6分钟到家.3.王强在电脑上进行高尔夫球的模拟练习,在某处按函数关系式 y= 击球,球正好进洞.
其中,y(m)是球的飞行高度,x(m)是球飞出的水平距离.
(1)试画出高尔夫球飞行的路线;
(2)从图象上看,高尔夫球的最大飞行高度是多少?球的起点与洞之间的距离是多少?由函数解析式画函数图象,一般按下列步骤进行:
1.列表:列表给出自变量与函数的一些对应值;
2.描点:以表中对应值为坐标,在坐标平面内描出相应的点;
3.连线:按照自变量由小到大的顺序,把所描各点用光滑的曲线连结起来.
描出的点越多,图象越精确.有时不能把所有的点都描出,就用光滑的曲线连结画出的点,从而得到函数的近似的图象.1.从教材习题中选取,
2.完成练习册本课时的习题.构成我们学习最大障碍的是已知的东西,而不是未知的东西。
—— 贝尔纳
你能利用函数解析式画出一些函数的图象吗?探究1:画函数图象画出函数y= 的图象描点:用光滑曲线连线:【归纳结论】画函数图象的方法,可以概括为列表、描点、连线三步,通常称为描点法.探究2:利用函数图象解决实际问题
王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上山,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分)之间的S函数关系(从小强开始爬山时计时).看图回答问题.1.小强让爷爷先上多少米?
2.山顶离山脚的距离有多少米?谁先爬上山顶?
3.小强通过多少时间追上爷爷?【分析】
在观察实际问题的图象时,先从两坐标轴表示的实际意义得到点的坐标意义.再从图形中分析两变量的相互关系,寻找对应的现实情境.如图中的两条线段都可以看出随着自变量x的逐渐增大,函数值y也随着逐渐增大,再联系现实情境爬山所用时间越长,离开山脚的距离越大,当x达到最大值时,也就是到达山顶.
解:1.60米 2.300米 小强 3.8分1.画出函数y=x+1的图象
解:列表描点:连线:2.小明从家里出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家.下面的图描述了小明在散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.
请你由图具体说明小明散步的情况.解:小明先走了约3分钟,到达离家250米处的一个阅报栏前看了5分钟报,又向前走了2分钟,到达离家450米处返回,走了6分钟到家.3.王强在电脑上进行高尔夫球的模拟练习,在某处按函数关系式 y= 击球,球正好进洞.
其中,y(m)是球的飞行高度,x(m)是球飞出的水平距离.
(1)试画出高尔夫球飞行的路线;
(2)从图象上看,高尔夫球的最大飞行高度是多少?球的起点与洞之间的距离是多少?由函数解析式画函数图象,一般按下列步骤进行:
1.列表:列表给出自变量与函数的一些对应值;
2.描点:以表中对应值为坐标,在坐标平面内描出相应的点;
3.连线:按照自变量由小到大的顺序,把所描各点用光滑的曲线连结起来.
描出的点越多,图象越精确.有时不能把所有的点都描出,就用光滑的曲线连结画出的点,从而得到函数的近似的图象.1.从教材习题中选取,
2.完成练习册本课时的习题.构成我们学习最大障碍的是已知的东西,而不是未知的东西。
—— 贝尔纳
