17.3.1 一次函数 课件(22张PPT)
文档属性
| 名称 | 17.3.1 一次函数 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 184.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-31 16:41:26 | ||
图片预览





文档简介
课件22张PPT。第17章 函数及其 图象
17.3一次函数
2.一次函数的图象
根据画图象的基本步骤,要求学生分别画出y1=2x+1和y2=-2x+1的图象.xy01-1y1=2x+1y2=—2x+1在同一个平面直角坐标系中画出下列函数的图像:
(2)
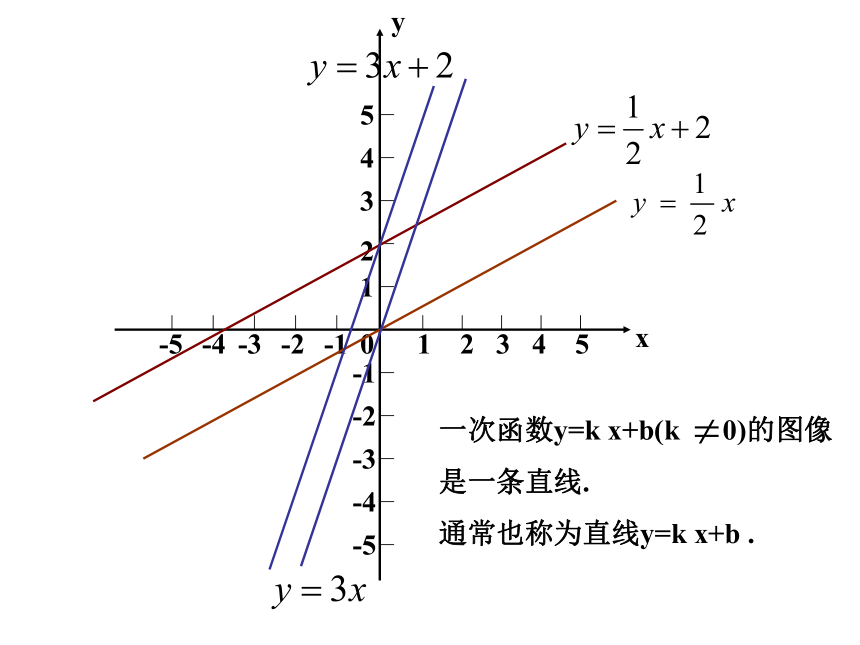
(3) (4)1-12345-4-3-2-512345-1-2-3-4-50观察:这些函数的图像
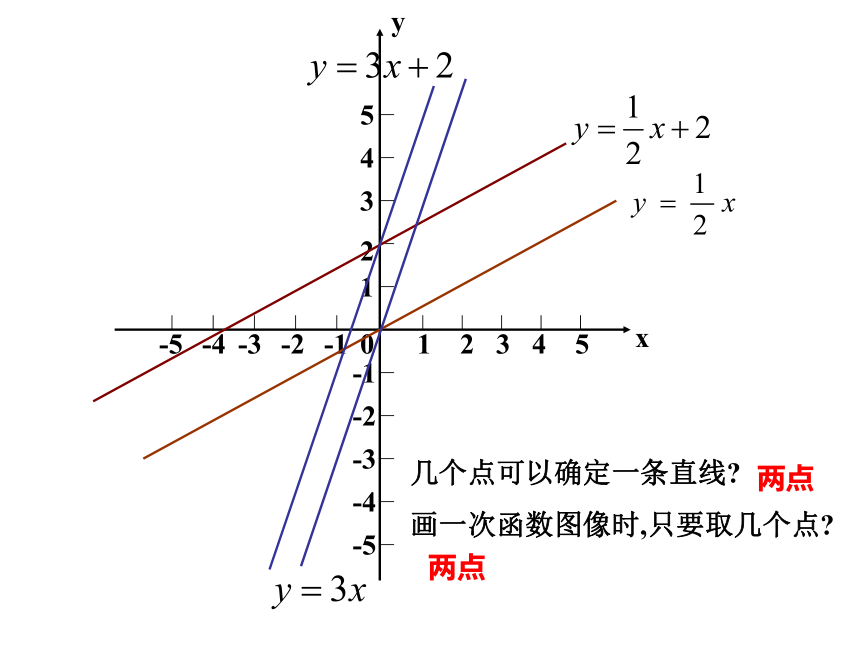
有什么特点?xy1-12345-4-3-2-512345-1-2-3-4-50yx1-12345-4-3-2-512345-1-2-3-4-50几个点可以确定一条直线?
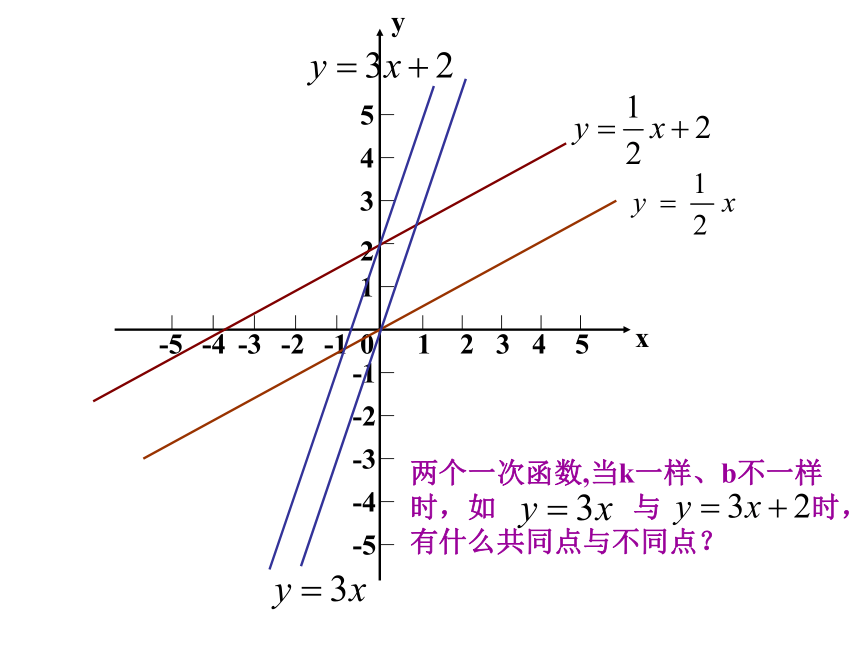
画一次函数图像时,只要取几个点?yx两点两点1-12345-4-3-2-512345-1-2-3-4-50两个一次函数,当k一样、b不一样时,如 与 时,有什么共同点与不同点?yx1-12345-4-3-2-512345-1-2-3-4-50两个一次函数,当k不一样、b一样
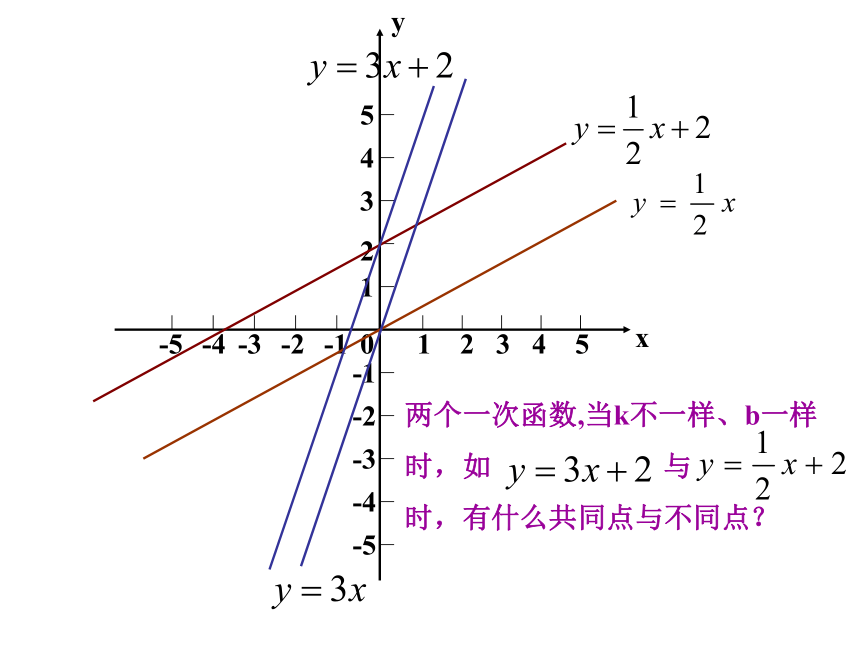
时,如 与
时,有什么共同点与不同点?yx【归纳】【归纳结论】
两个一次函数,当k一样,b不一样时.
共同点:直线平行,都是由直线y=kx(k≠0)向上或向下移动得到;
不同点:它们与y轴的交点不同.
而当两个一次函数,b一样,k不一样时.
共同点:它们与y轴交于同一点(0,b);
不同点:直线不平行.例1 已知关于x的函数y=(m-1)x|m|+n-3(1)当m和n取何值时,该函数是关于x的一次函数?解: 根据一次函数的定义可知:|m|=1,
且m-1≠0,故m=-1,且n为全体实数.例1 已知关于x的函数y=(m-1)x|m|+n-3(2)当m和n取何值时,该函数是关于x的正比例函数?解: 根据正比例函数的定义可知,在(1)的条件下
还要满足n-3=0,故m=-1,n=3. 例2 已知一次函数y=(6+3m)x+(m-4),y随x的增大而增大,函数的图象与y轴的交点在y轴的负半轴上,求m的取值范围.【分析】 根据一次函数的特征可知,6+3m>0,
m-4<0,解得 -2<m<4 例3 直线l1和直线l2在同一直角坐标系中的位置如图所示,点P1(x1,y1)在直线l1上,点P3(x3,y3)在直线l2上,点P2(x2,y2)为直线l1,l2的交点,其中x2<x1,x2<x3则( ).
A.y1<y2<y3 B.y3<y1<y2 C. y3<y2<y1 D.y2<y1<y3【分析】 观察直线l1,y随x的增大而减小,因为x2<x1,则有y2>y1;观察直线l2知,y随x的增大而增大,因为x2<x3,则有y2<y3,故y1<y2<y3,故选A.xy0l1l2P2答案:选B2、已知一次函数y=mx+|m+1|的图象与y轴交于点(0,3),且y随x值的增大而增大,则m的值为( ).
A.2 B.-4 C. -2或-4 D.2或-4【答案】A3、已知一次函数y=mx-(m-2)过原点,
则m的值为( )
A.m>2 B.m<2
C.m=2 D.不能确定【答案】C 4、下列关系:
①面积一定的长方形的长s与宽a;
②圆的周长s与半径a;
③正方形的面积s与边长a;
④速度一定时行驶的路程s与行驶时间a,
其中s是a的正比例函数的有( )
A.1个 B.2个 C.3个 D.4个【答案】B5、函数y=kx+b的图象平行于直线y=-2x,且与
y轴交于点(0,3),则k= ,b= .3-26、已知点A(a+2,1-a)在函数y=2x-1的图象上,求a的值.1.一次函数的图象是一条直线.
2.画一次函数图象时,只要取两个点即可,一般取直线与x轴、y轴的交点比较简便.
3.两个一次函数,当k一样,b不一样时,共同之处是直线平行,都是由直线y=kx(k≠0)向上或向下移动得到,不同之处是它们与y轴的交点不同;
当b一样,k不一样时,共同之处是它们与y轴交于同一点(0,b),不同之处是直线不平行.4.一次函数y=kx+b,当x=0时,y=b;当y=0时,x= .所以直线y=kx+b与y轴的交点坐标是(0,b),与x轴的交点坐标是( ,0);
5.在画实际问题中的一次函数图象时,要考虑自变量的取值范围,画出的图象往往不再是一条直线.1.从教材习题中选取,
2.完成练习册本课时的习题.
(2)
(3) (4)1-12345-4-3-2-512345-1-2-3-4-50观察:这些函数的图像
有什么特点?xy1-12345-4-3-2-512345-1-2-3-4-50yx1-12345-4-3-2-512345-1-2-3-4-50几个点可以确定一条直线?
画一次函数图像时,只要取几个点?yx两点两点1-12345-4-3-2-512345-1-2-3-4-50两个一次函数,当k一样、b不一样时,如 与 时,有什么共同点与不同点?yx1-12345-4-3-2-512345-1-2-3-4-50两个一次函数,当k不一样、b一样
时,如 与
时,有什么共同点与不同点?yx【归纳】【归纳结论】
两个一次函数,当k一样,b不一样时.
共同点:直线平行,都是由直线y=kx(k≠0)向上或向下移动得到;
不同点:它们与y轴的交点不同.
而当两个一次函数,b一样,k不一样时.
共同点:它们与y轴交于同一点(0,b);
不同点:直线不平行.例1 已知关于x的函数y=(m-1)x|m|+n-3(1)当m和n取何值时,该函数是关于x的一次函数?解: 根据一次函数的定义可知:|m|=1,
且m-1≠0,故m=-1,且n为全体实数.例1 已知关于x的函数y=(m-1)x|m|+n-3(2)当m和n取何值时,该函数是关于x的正比例函数?解: 根据正比例函数的定义可知,在(1)的条件下
还要满足n-3=0,故m=-1,n=3. 例2 已知一次函数y=(6+3m)x+(m-4),y随x的增大而增大,函数的图象与y轴的交点在y轴的负半轴上,求m的取值范围.【分析】 根据一次函数的特征可知,6+3m>0,
m-4<0,解得 -2<m<4 例3 直线l1和直线l2在同一直角坐标系中的位置如图所示,点P1(x1,y1)在直线l1上,点P3(x3,y3)在直线l2上,点P2(x2,y2)为直线l1,l2的交点,其中x2<x1,x2<x3则( ).
A.y1<y2<y3 B.y3<y1<y2 C. y3<y2<y1 D.y2<y1<y3【分析】 观察直线l1,y随x的增大而减小,因为x2<x1,则有y2>y1;观察直线l2知,y随x的增大而增大,因为x2<x3,则有y2<y3,故y1<y2<y3,故选A.xy0l1l2P2答案:选B2、已知一次函数y=mx+|m+1|的图象与y轴交于点(0,3),且y随x值的增大而增大,则m的值为( ).
A.2 B.-4 C. -2或-4 D.2或-4【答案】A3、已知一次函数y=mx-(m-2)过原点,
则m的值为( )
A.m>2 B.m<2
C.m=2 D.不能确定【答案】C 4、下列关系:
①面积一定的长方形的长s与宽a;
②圆的周长s与半径a;
③正方形的面积s与边长a;
④速度一定时行驶的路程s与行驶时间a,
其中s是a的正比例函数的有( )
A.1个 B.2个 C.3个 D.4个【答案】B5、函数y=kx+b的图象平行于直线y=-2x,且与
y轴交于点(0,3),则k= ,b= .3-26、已知点A(a+2,1-a)在函数y=2x-1的图象上,求a的值.1.一次函数的图象是一条直线.
2.画一次函数图象时,只要取两个点即可,一般取直线与x轴、y轴的交点比较简便.
3.两个一次函数,当k一样,b不一样时,共同之处是直线平行,都是由直线y=kx(k≠0)向上或向下移动得到,不同之处是它们与y轴的交点不同;
当b一样,k不一样时,共同之处是它们与y轴交于同一点(0,b),不同之处是直线不平行.4.一次函数y=kx+b,当x=0时,y=b;当y=0时,x= .所以直线y=kx+b与y轴的交点坐标是(0,b),与x轴的交点坐标是( ,0);
5.在画实际问题中的一次函数图象时,要考虑自变量的取值范围,画出的图象往往不再是一条直线.1.从教材习题中选取,
2.完成练习册本课时的习题.
