17.5 实践与探索 第二课时 课件
文档属性
| 名称 | 17.5 实践与探索 第二课时 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 73.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-31 16:41:26 | ||
图片预览



文档简介
课件11张PPT。第2课时17.5 实践与探索情境导入观察课本第60页图17.5.2.
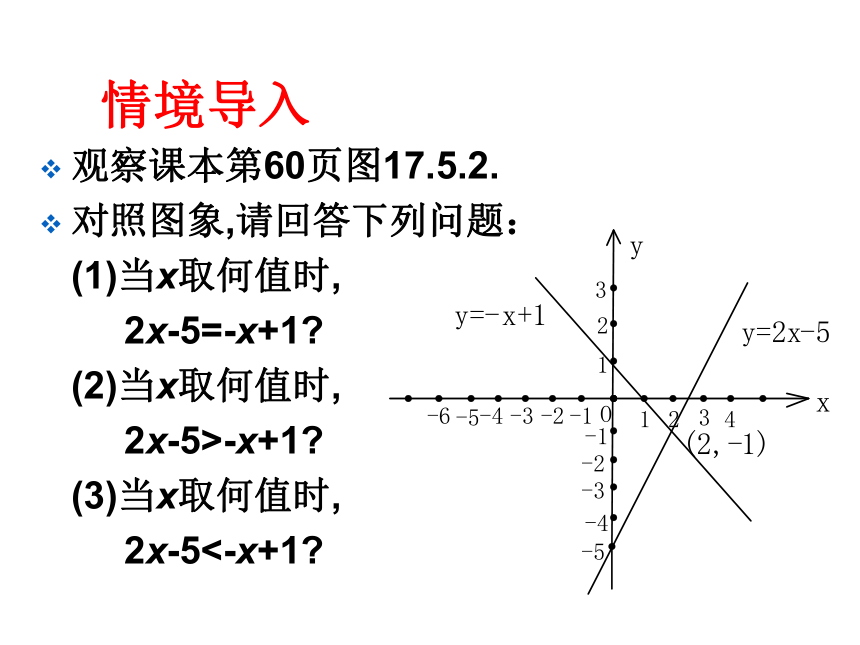
对照图象,请回答下列问题:
(1)当x取何值时,
2x-5=-x+1?
(2)当x取何值时,
2x-5>-x+1?
(3)当x取何值时,
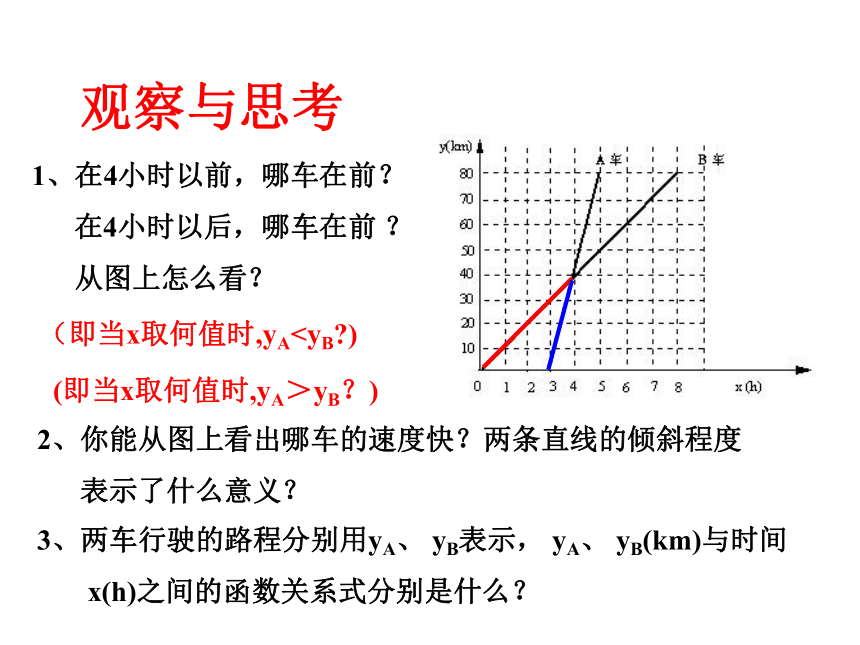
2x-5<-x+1?1、在4小时以前,哪车在前?
在4小时以后,哪车在前 ?
从图上怎么看? 2、你能从图上看出哪车的速度快?两条直线的倾斜程度
表示了什么意义?3、两车行驶的路程分别用yA、 yB表示, yA、 yB(km)与时间
x(h)之间的函数关系式分别是什么? (即当x取何值时,yA>yB?)(即当x取何值时,yA(1)10x>40x-120
(yA>yB)
(2)10x<40x-120
( yA<yB)思维拓展探究并思考画出函数 的图象,
根据图象,指出:
(1)x取什么值时,函数值y等于零?
(2)x取什么值时,函数值y始终大于零?实践运用例1 画出函数y=-x-2的图象,
根据图象,指出:
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y始终大于零?解:过(-2,0),(0,-2)作直线,如图.(1)当x=-2时,y=0;
(2)当x<-2时,y>0.例2 利用图象解不等式:
(1)2x-5>-x+1,
(2) 2x-5<-x+1.解:设y1=2x-5,y2=-x+1,在直角坐标系中画出这两条直线,如图.两条直线的交点坐标是(2, -1) ,可知:
(1)2x-5>-x+1的解集是y1>y2时
x的取值范围,为x>2;
(2)2x-5<-x+1的解集是y1<y2时
x的取值范围,为x<2.反馈练习1.已知函数y=4x-3.当x取何值时,函数的
图象在第四象限?
2.画出函数y=3x-6的图象,根据图象,指出:
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y大于零?
(3) x取什么值时,函数值 y小于零?3.画出函数y=-0.5x-1的图象,根据图象,求:
(1)函数图象与x轴的交点坐标;
(2)函数图象在x轴上方时,x的取值范围;
(3)函数图象在x轴下方时,x的取值范围.4.如图,一次函数y=kx+b的图象与反比例函数(1)利用图中条件,求反比例
函数和一次函数的解析式;
(2)根据图象写出一次函数的
值大于反比例函数的值的x
的取值范围. 题后小结:1、从刚才的例子中我们应该总结一下, 我们用到了哪些解决问题的方法?1) 图象法;2)数形结合法.2、在观察图形时主要看图形中的哪几个关键地方? 1) 两坐标轴的含义;2)两直线的交点;
3)与坐标轴的交点; 4)图象的高低;
5)直线的倾斜程度.3、利用函数的图象我们刚才解决了哪几个问题?求不等式的解集.
对照图象,请回答下列问题:
(1)当x取何值时,
2x-5=-x+1?
(2)当x取何值时,
2x-5>-x+1?
(3)当x取何值时,
2x-5<-x+1?1、在4小时以前,哪车在前?
在4小时以后,哪车在前 ?
从图上怎么看? 2、你能从图上看出哪车的速度快?两条直线的倾斜程度
表示了什么意义?3、两车行驶的路程分别用yA、 yB表示, yA、 yB(km)与时间
x(h)之间的函数关系式分别是什么? (即当x取何值时,yA>yB?)(即当x取何值时,yA
(yA>yB)
(2)10x<40x-120
( yA<yB)思维拓展探究并思考画出函数 的图象,
根据图象,指出:
(1)x取什么值时,函数值y等于零?
(2)x取什么值时,函数值y始终大于零?实践运用例1 画出函数y=-x-2的图象,
根据图象,指出:
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y始终大于零?解:过(-2,0),(0,-2)作直线,如图.(1)当x=-2时,y=0;
(2)当x<-2时,y>0.例2 利用图象解不等式:
(1)2x-5>-x+1,
(2) 2x-5<-x+1.解:设y1=2x-5,y2=-x+1,在直角坐标系中画出这两条直线,如图.两条直线的交点坐标是(2, -1) ,可知:
(1)2x-5>-x+1的解集是y1>y2时
x的取值范围,为x>2;
(2)2x-5<-x+1的解集是y1<y2时
x的取值范围,为x<2.反馈练习1.已知函数y=4x-3.当x取何值时,函数的
图象在第四象限?
2.画出函数y=3x-6的图象,根据图象,指出:
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y大于零?
(3) x取什么值时,函数值 y小于零?3.画出函数y=-0.5x-1的图象,根据图象,求:
(1)函数图象与x轴的交点坐标;
(2)函数图象在x轴上方时,x的取值范围;
(3)函数图象在x轴下方时,x的取值范围.4.如图,一次函数y=kx+b的图象与反比例函数(1)利用图中条件,求反比例
函数和一次函数的解析式;
(2)根据图象写出一次函数的
值大于反比例函数的值的x
的取值范围. 题后小结:1、从刚才的例子中我们应该总结一下, 我们用到了哪些解决问题的方法?1) 图象法;2)数形结合法.2、在观察图形时主要看图形中的哪几个关键地方? 1) 两坐标轴的含义;2)两直线的交点;
3)与坐标轴的交点; 4)图象的高低;
5)直线的倾斜程度.3、利用函数的图象我们刚才解决了哪几个问题?求不等式的解集.
