2018-2019学年山东省青岛三十九中九年级(下)期初数学试卷解析版
文档属性
| 名称 | 2018-2019学年山东省青岛三十九中九年级(下)期初数学试卷解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 270.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-31 23:58:48 | ||
图片预览


文档简介
2018-2019学年山东省青岛三十九中九年级(下)期初数学试卷
一、选择题:(每题3分共24分)
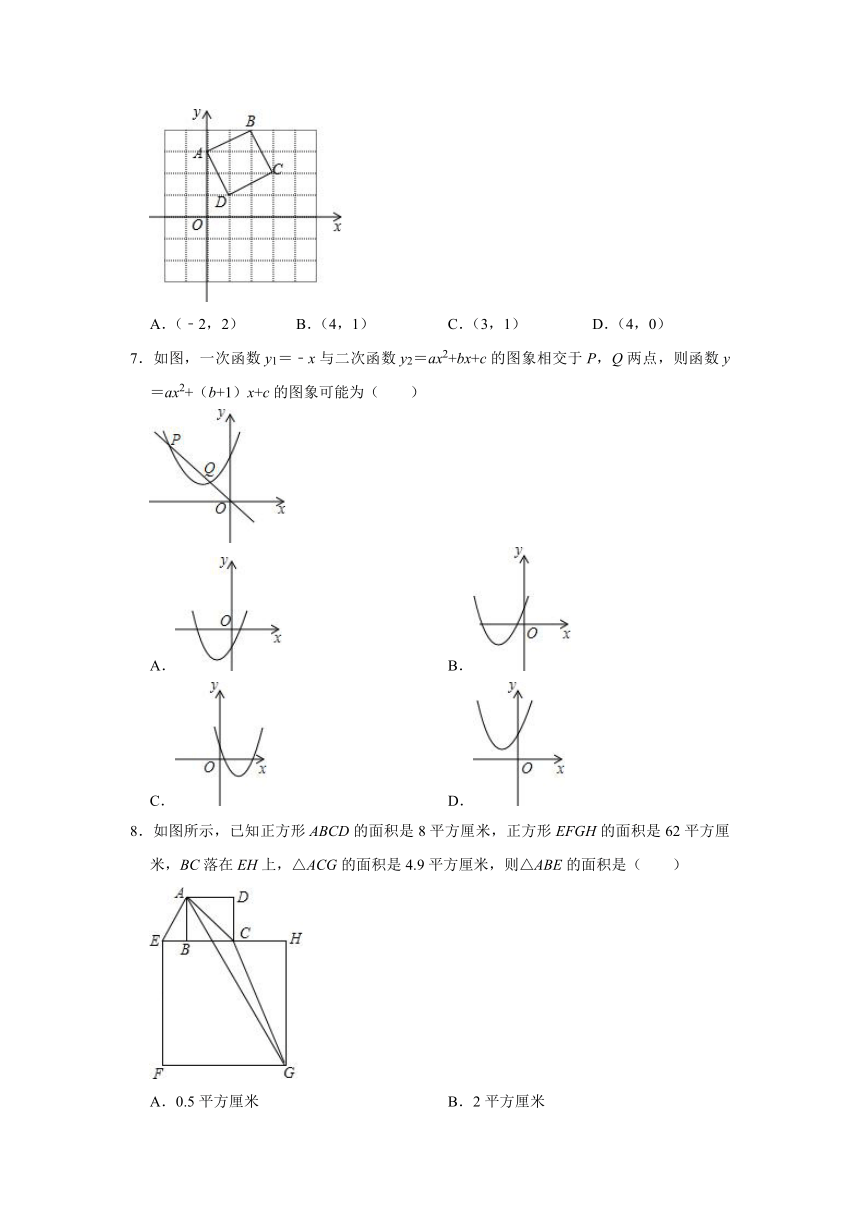
1.下列四个图案中,不是轴对称图案的是( )
A. B.
C. D.
2.地球与月球之间的平均距离大约为384000km,384000用科学记数法可表示为( )
A.3.84×103 B.3.84×104 C.3.84×105 D.3.84×106
3.如图,数轴上点A表示数a,则﹣a表示数的是( )
A.2 B.1 C.﹣1 D.﹣2
4.计算(a2)3÷(a2?a3)的结果是( )
A.0 B.1 C.a D.a3
5.如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )
A.AE=EF B.AB=2DE
C.△ADF和△ADE的面积相等 D.△ADE和△FDE的面积相等
6.正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
A.(﹣2,2) B.(4,1) C.(3,1) D.(4,0)
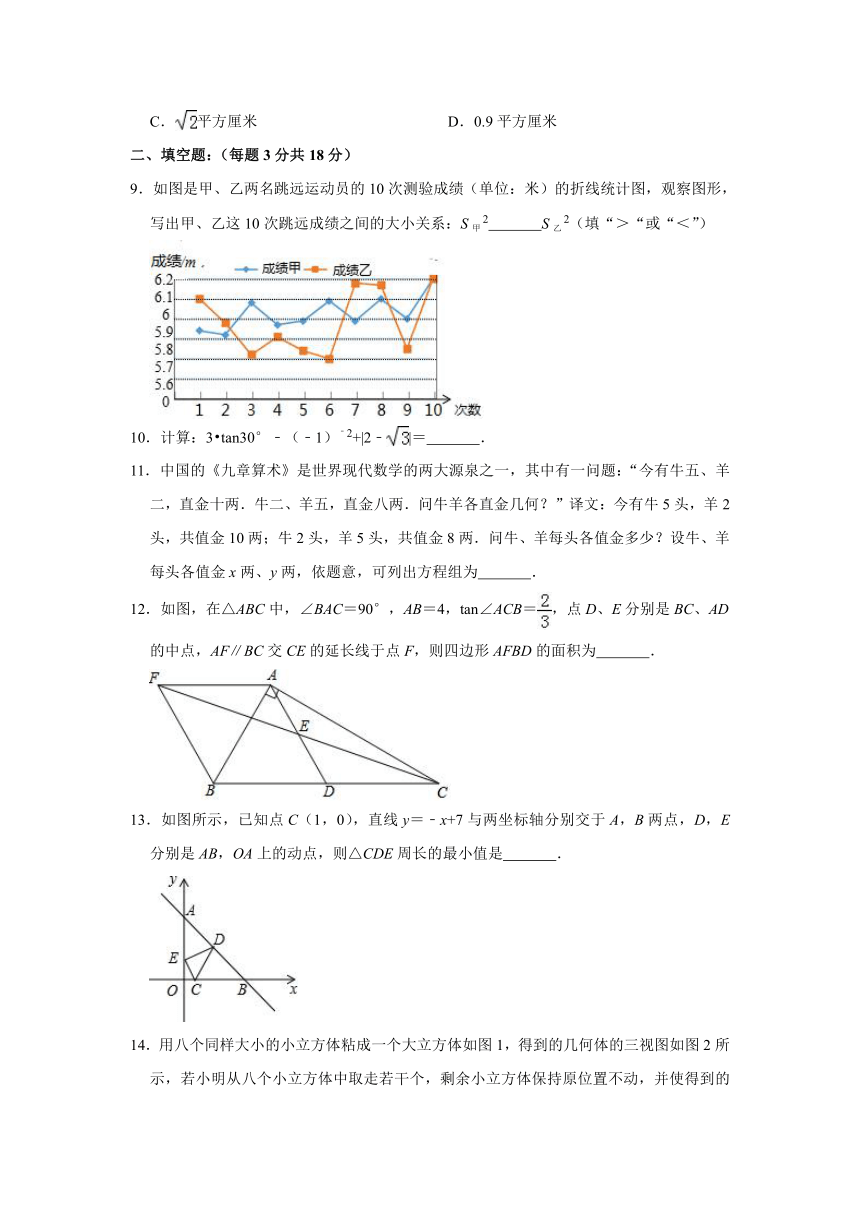
7.如图,一次函数y1=﹣x与二次函数y2=ax2+bx+c的图象相交于P,Q两点,则函数y=ax2+(b+1)x+c的图象可能为( )
A. B.
C. D.
8.如图所示,已知正方形ABCD的面积是8平方厘米,正方形EFGH的面积是62平方厘米,BC落在EH上,△ACG的面积是4.9平方厘米,则△ABE的面积是( )
A.0.5平方厘米 B.2平方厘米
C.平方厘米 D.0.9平方厘米
二、填空题:(每题3分共18分)
9.如图是甲、乙两名跳远运动员的10次测验成绩(单位:米)的折线统计图,观察图形,写出甲、乙这10次跳远成绩之间的大小关系:S甲2 S乙2(填“>“或“<”)
10.计算:3?tan30°﹣(﹣1)﹣2+|2﹣|= .
11.中国的《九章算术》是世界现代数学的两大源泉之一,其中有一问题:“今有牛五、羊二,直金十两.牛二、羊五,直金八两.问牛羊各直金几何?”译文:今有牛5头,羊2头,共值金10两;牛2头,羊5头,共值金8两.问牛、羊每头各值金多少?设牛、羊每头各值金x两、y两,依题意,可列出方程组为 .
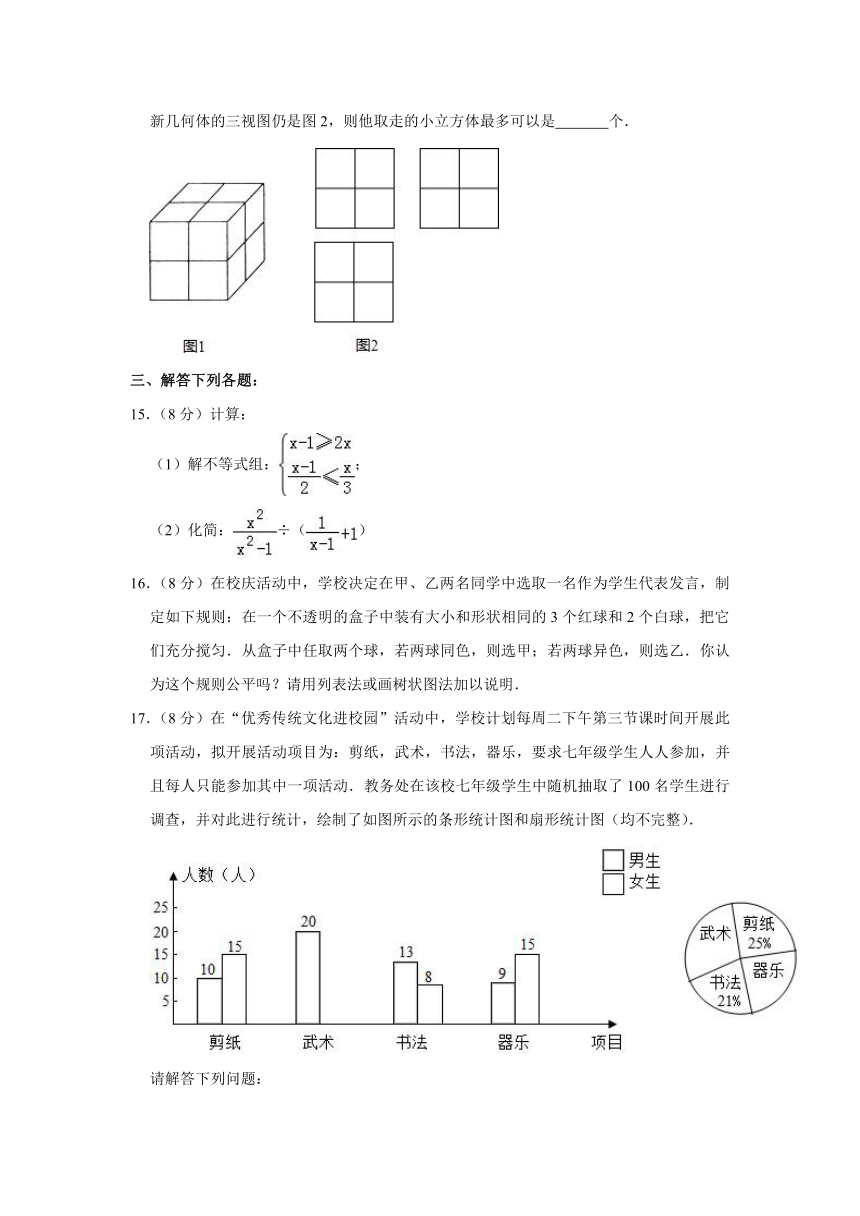
12.如图,在△ABC中,∠BAC=90°,AB=4,tan∠ACB=,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于点F,则四边形AFBD的面积为 .
13.如图所示,已知点C(1,0),直线y=﹣x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是 .
14.用八个同样大小的小立方体粘成一个大立方体如图1,得到的几何体的三视图如图2所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图2,则他取走的小立方体最多可以是 个.
三、解答下列各题:
15.(8分)计算:
(1)解不等式组:;
(2)化简:÷()
16.(8分)在校庆活动中,学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
17.(8分)在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).
请解答下列问题:
(1)请补全条形统计图和扇形统计图;
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?
(3)若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?
18.(10分)某公园的人工湖边上有一座假山,假山顶上有一竖起的建筑物CD,高为10米,数学小组为了测量假山的高度DE,在公园找了一水平地面,在A处测得建筑物点D(即山顶)的仰角为35°,沿水平方向前进20米到达B点,测得建筑物顶部C点的仰角为45°,求假山的高度DE.(结果精确到1米,参考数据:sin35°≈,cos35°≈,tan35°≈)
19.(10分)已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
20.(10分)山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?
(2)该车行计划新进一批A型车和新款B型车共60辆,要使这批车获利不少于33000元,A型车至多进多少辆?A,B两种型号车的进货和销售价格如表:
A型车
B型车
进货价格(元)
1100
1400
销售价格(元)
今年的销售价格
2000
21.(12分)某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD表示该产品每千克生产成本y1(单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
(1)请解释图中点D的横坐标、纵坐标的实际意义.
(2)求线段AB所表示的y1与x之间的函数表达式.
(3)当0≤x≤90时,销售该产品获得的利润与产量的关系式是 ;
当90≤x≤130时,销售该产品获得的利润与产量的关系式是 ;
总之,当产量为 kg时,获得的利润最大,最大利润是 .
22.(12分)已知:如图,在矩形ABCD中,AC是对角线,AB=8cm,BC=6cm.点P从点A出发,沿AC方向匀速运动,速度为2cm/s,同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s.过点P作PM⊥AD于点M,连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,点Q在线段AC的中垂线上;
(2)写出四边形PQAM的面积为S(cm2)与时间t的函数关系式;
(3)是否存在某一时刻t,使S四边形PQAM:S矩形ABCD=9:50?若存在,求出t的值;若不存在,请说明理由;
(4)当t为何值时,△APQ与△ADC相似.
2018-2019学年山东省青岛三十九中九年级(下)期初数学试卷
参考答案与试题解析
一、选择题:(每题3分共24分)
1.【解答】解:A、是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项正确;
C、是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项错误.
故选:B.
2.【解答】解:384 000=3.84×105.
故选:C.
3.【解答】解:由题意a=﹣2,
∴﹣a=2,
∴﹣a表示数的是2,
故选:A.
4.【解答】解:(a2)3÷(a2?a3)
=a6÷a5
=a.
故选:C.
5.【解答】解:如图,连接CF,
∵点D是BC中点,
∴BD=CD,
由折叠知,∠ACB=∠DFE,CD=DF,
∴BD=CD=DF,
∴△BFC是直角三角形,
∴∠BFC=90°,
∵BD=DF,
∴∠B=∠BFD,
∴∠EAF=∠B+∠ACB=∠BFD+∠DFE=∠AFE,
∴AE=EF,故A正确,
由折叠知,EF=CE,
∴AE=CE,
∵BD=CD,
∴DE是△ABC的中位线,
∴AB=2DE,故B正确,
∵AE=CE,
∴S△ADE=S△CDE,
由折叠知,△CDE≌△FDE,
∴S△CDE=S△FDE,
∴S△ADE=S△FDE,故D正确,
当AD=AC时,△ADF和△ADE的面积相等
∴C选项不一定正确,
故选:C.
6.【解答】解:如图,正方形ABCD绕D点顺时针旋转90°得到正方形CB′C′D,即旋转后B点的坐标为(4,0).
故选:D.
7.【解答】解:∵一次函数y1=﹣x与二次函数y2=ax2+bx+c图象相交于P、Q两点,
∴方程ax2+(b+1)x+c=0有两个不相等的根,
∴函数y=ax2+(b+1)x+c与x轴有两个交点,
∵﹣<0,a>0
∴﹣=﹣﹣<0
∴函数y=ax2+(b+1)x+c的对称轴x=﹣<0,
∵a>0,开口向上,与y轴交点在正半轴.
故选:B.
8.【解答】解:延长AB与FG交于点M,如图所示:
设正方形ABCD的边长为a厘米,EB=b厘米,CH=c厘米,
则AB=BC=a厘米,BM=EH=EB+BC+CH=(a+b+c)厘米,MG=BH=(a+c)厘米,
∵S△ACG=S△ABC+S梯形BCGM﹣S△AMG=4.9,
∴a2+(a+b+c)(2a+c)﹣(2a+b+c)(a+c)=4.9,
整理得:a2+ab=4.9,
又正方形ABCD的面积为8平方厘米,即a2=8,
∴S△ABE=AB?EB=ab=4.9﹣×8=4.9﹣4=0.9(平方厘米).
故选:D.
二、填空题:(每题3分共18分)
9.【解答】解:由图可得,甲这10次跳远成绩离散程度小,而乙这10次跳远成绩离散程度大,
∴S甲2<S乙2,
故答案为:<.
10.【解答】解:原式=3×﹣1+2﹣
=﹣1+2﹣
=1,
故答案为:1.
11.【解答】解:设每头牛值金x两,每头羊值金y两,
根据题意得:.
故答案为:.
12.【解答】解:∵AF∥BC,
∴∠AFC=∠FCD,
在△AEF与△DEC中,
,
∴△AEF≌△DEC(AAS).
∴AF=DC,
∵BD=DC,
∴AF=BD,
∴四边形AFBD是平行四边形,
∴S四边形AFBD=2S△ABD,
又∵BD=DC,
∴S△ABC=2S△ABD,
∴S四边形AFBD=S△ABC,
∵∠BAC=90°,tan∠ACB=,AB=4,
∴AC==6,
∴S△ABC=AB?AC=×4×6=12,
∴S四边形AFBD=12.
故答案为:12.
13.【解答】解:如图,点C关于OA的对称点C′(﹣1,0),点C关于直线AB的对称点C″,
∵直线AB的解析式为y=﹣x+7,
∴直线CC″的解析式为y=x﹣1,
由解得,
∴直线AB与直线CC″的交点坐标为K(4,3),
∵K是CC″中点,
∴可得C″(7,6).
连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,
△DEC的周长=DE+EC+CD=EC′+ED+DC″=C′C″==10.
故答案为10.
14.【解答】解:由主视图和左视图可得每一层的每一行每一列都要保留一个立方体,
故取走的小立方体最多可以是4个.
具体可参看图形:
故答案为:4.
三、解答下列各题:
15.【解答】解:(1)
解不等式①,得x≤﹣1,
解不等式②,得x≤3,
故原不等式组的解集是x≤﹣1;
(2)÷()
=÷
=?
=.
16.【解答】解:如图所示:
,
由树状图可得:一共有20种可能,两球同色的有8种情况,故选择甲的概率为:=;
则选择乙的概率为:,
故此游戏不公平.
17.【解答】解:(1)由条形图知,男生共有:10+20+13+9=52人,
∴女生人数为100﹣52=48人,
∴参加武术的女生为48﹣15﹣8﹣15=10人,
∴参加武术的人数为20+10=30人,
∴30÷100=30%,
参加器乐的人数为9+15=24人,
∴24÷100=24%,
补全条形统计图和扇形统计图如图所示:
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是.
答:在参加“剪纸”活动项目的学生中,男生所占的百分比为40%.
(3)500×21%=105(人).
答:估计其中参加“书法”项目活动的有105人.
(4).
答:正好抽到参加“器乐”活动项目的女生的概率为.
18.【解答】解:过点D作水平线的垂线,即(DE⊥AB),垂足为E,则C、D、E在一条直线上,
设DE的长为x米,
在Rt△BCE中,∠CBE=45°,
∴CE=BE=CD+DE=(10+x)米,
在Rt△ADE中,∠A=35°,
AE=AB+BE=20+10+x=30+x,
tanA=,
∴tan35°=≈,
解得:x≈70,
答:假山的高度DE约为70米.
19.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠AFC=∠DCG,
∵GA=GD,∠AGF=∠CGD,
∴△AGF≌△DGC,
∴AF=CD,
∴AB=AF.
(2)解:结论:四边形ACDF是矩形.
理由:∵AF=CD,AF∥CD,
∴四边形ACDF是平行四边形,
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD=120°,
∴∠FAG=60°,
∵AB=AG=AF,
∴△AFG是等边三角形,
∴AG=GF,
∵△AGF≌△DGC,
∴FG=CG,∵AG=GD,
∴AD=CF,
∴四边形ACDF是矩形.
20.【解答】解:(1)设今年A型车每辆售价x元,则去年售价每辆为(x+400)元,由题意,得:
=,
解得:x=1600.
经检验,x=1600是原方程的根.
答:今年A型车每辆售价1600元;
(2)设今年新进A型车a辆,则B型车(60﹣a)辆,由题意,得
(1600﹣1100)a+(2000﹣1400)(60﹣a)≥33000,
解得:a≤30,
故要使这批车获利不少于33000元,A型车至多进30辆.
21.【解答】解:(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;
(2)设线段AB所表示的y1与x之间的函数关系式为y=k1x+b1,
∵y=k1x+b1的图象过点(0,60)与(90,42),
∴,
∴解得:,
∴这个一次函数的表达式为;y=﹣0.2x+60(0≤x≤90);
(3)设y2与x之间的函数关系式为y=k2x+b2,
∵经过点(0,120)与(130,42),
∴,
解得:,
∴这个一次函数的表达式为y2=﹣0.6x+120(0≤x≤130),
设产量为xkg时,获得的利润为W元,
当0≤x≤90时,W=x[(﹣0.6x+120)﹣(﹣0.2x+60)]=﹣0.4(x﹣75)2+2250,
∴当x=75时,W的值最大,最大值为2250;
当90≤x≤130时,W=x[(﹣0.6x+120)﹣42]=﹣0.6(x﹣65)2+2535,
由﹣0.6<0知,当x>65时,W随x的增大而减小,∴90≤x≤130时,W≤2160,
∴当x=90时,W=﹣0.6(90﹣65)2+2535=2160,
因此当该产品产量为75kg时,获得的利润最大,最大值为2250.
故答案为:w=﹣0.4(x﹣75)2+2250;w=﹣0.6(x﹣65)2+2535,75,2250.
22.【解答】解:(1)由题意CQ=AQ=8﹣2t,
在Rt△BCQ中,∵BC2+BQ2=CQ2,
∴62+(2t)2=(8﹣2t)2,
解得t=.
(2)∵四边形ABCD是矩形,
∴S矩形ABCD=AB?BC=8×6=48,
∵PM⊥AD,CD⊥AD,
∴PM∥CD,
∴△APM∽△ACD,
∴==,
即 ==,
解得AM=t,PM=t,
∴S△APM=AM?PM=×t×t=t2.
∵sin∠PAQ==,
∴S△APQ=AP?AQ?sin∠PAQ=×2t(8﹣2t)×=t(4﹣t),
∵S四边形PQAM=t2+t(4﹣t)=﹣t2+t.
(3)存在t=2,使S四边形PQAM=S矩形ABCD.
如图2,
,
∵S四边形PQAM=S矩形ABCD,
∴t2+t(4﹣t)=×48,
整理,可得t2﹣20t+36=0
解得t=2或t=18(舍去),
∴存在t=2,使S四边形PQAM=S矩形ABCD.
(4)当t=2或1时,△APQ与△ABC相似.
①当△APQ∽△ACB,
∴=,
即 =,
解得t=2,
②如图3,
,
当∠APQ=90°时,△APQ与△ABC相似,
∵tan∠PAQ==,
∴=,
即 =,
∴PQ=t,
∵BQ=2t,
∴AQ=8﹣2t,
在Rt△APQ中,
∵AP2+PQ2=AQ2,
∴(2t)2+(t)2=(8﹣2t)2,
解得t=1或t=﹣16(舍去).
综上,可得
当t=2或1时,△APQ与△ABC相似.
一、选择题:(每题3分共24分)
1.下列四个图案中,不是轴对称图案的是( )
A. B.
C. D.
2.地球与月球之间的平均距离大约为384000km,384000用科学记数法可表示为( )
A.3.84×103 B.3.84×104 C.3.84×105 D.3.84×106
3.如图,数轴上点A表示数a,则﹣a表示数的是( )
A.2 B.1 C.﹣1 D.﹣2
4.计算(a2)3÷(a2?a3)的结果是( )
A.0 B.1 C.a D.a3
5.如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )
A.AE=EF B.AB=2DE
C.△ADF和△ADE的面积相等 D.△ADE和△FDE的面积相等
6.正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
A.(﹣2,2) B.(4,1) C.(3,1) D.(4,0)
7.如图,一次函数y1=﹣x与二次函数y2=ax2+bx+c的图象相交于P,Q两点,则函数y=ax2+(b+1)x+c的图象可能为( )
A. B.
C. D.
8.如图所示,已知正方形ABCD的面积是8平方厘米,正方形EFGH的面积是62平方厘米,BC落在EH上,△ACG的面积是4.9平方厘米,则△ABE的面积是( )
A.0.5平方厘米 B.2平方厘米
C.平方厘米 D.0.9平方厘米
二、填空题:(每题3分共18分)
9.如图是甲、乙两名跳远运动员的10次测验成绩(单位:米)的折线统计图,观察图形,写出甲、乙这10次跳远成绩之间的大小关系:S甲2 S乙2(填“>“或“<”)
10.计算:3?tan30°﹣(﹣1)﹣2+|2﹣|= .
11.中国的《九章算术》是世界现代数学的两大源泉之一,其中有一问题:“今有牛五、羊二,直金十两.牛二、羊五,直金八两.问牛羊各直金几何?”译文:今有牛5头,羊2头,共值金10两;牛2头,羊5头,共值金8两.问牛、羊每头各值金多少?设牛、羊每头各值金x两、y两,依题意,可列出方程组为 .
12.如图,在△ABC中,∠BAC=90°,AB=4,tan∠ACB=,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于点F,则四边形AFBD的面积为 .
13.如图所示,已知点C(1,0),直线y=﹣x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是 .
14.用八个同样大小的小立方体粘成一个大立方体如图1,得到的几何体的三视图如图2所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图2,则他取走的小立方体最多可以是 个.
三、解答下列各题:
15.(8分)计算:
(1)解不等式组:;
(2)化简:÷()
16.(8分)在校庆活动中,学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
17.(8分)在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).
请解答下列问题:
(1)请补全条形统计图和扇形统计图;
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?
(3)若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?
18.(10分)某公园的人工湖边上有一座假山,假山顶上有一竖起的建筑物CD,高为10米,数学小组为了测量假山的高度DE,在公园找了一水平地面,在A处测得建筑物点D(即山顶)的仰角为35°,沿水平方向前进20米到达B点,测得建筑物顶部C点的仰角为45°,求假山的高度DE.(结果精确到1米,参考数据:sin35°≈,cos35°≈,tan35°≈)
19.(10分)已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
20.(10分)山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?
(2)该车行计划新进一批A型车和新款B型车共60辆,要使这批车获利不少于33000元,A型车至多进多少辆?A,B两种型号车的进货和销售价格如表:
A型车
B型车
进货价格(元)
1100
1400
销售价格(元)
今年的销售价格
2000
21.(12分)某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD表示该产品每千克生产成本y1(单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
(1)请解释图中点D的横坐标、纵坐标的实际意义.
(2)求线段AB所表示的y1与x之间的函数表达式.
(3)当0≤x≤90时,销售该产品获得的利润与产量的关系式是 ;
当90≤x≤130时,销售该产品获得的利润与产量的关系式是 ;
总之,当产量为 kg时,获得的利润最大,最大利润是 .
22.(12分)已知:如图,在矩形ABCD中,AC是对角线,AB=8cm,BC=6cm.点P从点A出发,沿AC方向匀速运动,速度为2cm/s,同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s.过点P作PM⊥AD于点M,连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,点Q在线段AC的中垂线上;
(2)写出四边形PQAM的面积为S(cm2)与时间t的函数关系式;
(3)是否存在某一时刻t,使S四边形PQAM:S矩形ABCD=9:50?若存在,求出t的值;若不存在,请说明理由;
(4)当t为何值时,△APQ与△ADC相似.
2018-2019学年山东省青岛三十九中九年级(下)期初数学试卷
参考答案与试题解析
一、选择题:(每题3分共24分)
1.【解答】解:A、是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项正确;
C、是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项错误.
故选:B.
2.【解答】解:384 000=3.84×105.
故选:C.
3.【解答】解:由题意a=﹣2,
∴﹣a=2,
∴﹣a表示数的是2,
故选:A.
4.【解答】解:(a2)3÷(a2?a3)
=a6÷a5
=a.
故选:C.
5.【解答】解:如图,连接CF,
∵点D是BC中点,
∴BD=CD,
由折叠知,∠ACB=∠DFE,CD=DF,
∴BD=CD=DF,
∴△BFC是直角三角形,
∴∠BFC=90°,
∵BD=DF,
∴∠B=∠BFD,
∴∠EAF=∠B+∠ACB=∠BFD+∠DFE=∠AFE,
∴AE=EF,故A正确,
由折叠知,EF=CE,
∴AE=CE,
∵BD=CD,
∴DE是△ABC的中位线,
∴AB=2DE,故B正确,
∵AE=CE,
∴S△ADE=S△CDE,
由折叠知,△CDE≌△FDE,
∴S△CDE=S△FDE,
∴S△ADE=S△FDE,故D正确,
当AD=AC时,△ADF和△ADE的面积相等
∴C选项不一定正确,
故选:C.
6.【解答】解:如图,正方形ABCD绕D点顺时针旋转90°得到正方形CB′C′D,即旋转后B点的坐标为(4,0).
故选:D.
7.【解答】解:∵一次函数y1=﹣x与二次函数y2=ax2+bx+c图象相交于P、Q两点,
∴方程ax2+(b+1)x+c=0有两个不相等的根,
∴函数y=ax2+(b+1)x+c与x轴有两个交点,
∵﹣<0,a>0
∴﹣=﹣﹣<0
∴函数y=ax2+(b+1)x+c的对称轴x=﹣<0,
∵a>0,开口向上,与y轴交点在正半轴.
故选:B.
8.【解答】解:延长AB与FG交于点M,如图所示:
设正方形ABCD的边长为a厘米,EB=b厘米,CH=c厘米,
则AB=BC=a厘米,BM=EH=EB+BC+CH=(a+b+c)厘米,MG=BH=(a+c)厘米,
∵S△ACG=S△ABC+S梯形BCGM﹣S△AMG=4.9,
∴a2+(a+b+c)(2a+c)﹣(2a+b+c)(a+c)=4.9,
整理得:a2+ab=4.9,
又正方形ABCD的面积为8平方厘米,即a2=8,
∴S△ABE=AB?EB=ab=4.9﹣×8=4.9﹣4=0.9(平方厘米).
故选:D.
二、填空题:(每题3分共18分)
9.【解答】解:由图可得,甲这10次跳远成绩离散程度小,而乙这10次跳远成绩离散程度大,
∴S甲2<S乙2,
故答案为:<.
10.【解答】解:原式=3×﹣1+2﹣
=﹣1+2﹣
=1,
故答案为:1.
11.【解答】解:设每头牛值金x两,每头羊值金y两,
根据题意得:.
故答案为:.
12.【解答】解:∵AF∥BC,
∴∠AFC=∠FCD,
在△AEF与△DEC中,
,
∴△AEF≌△DEC(AAS).
∴AF=DC,
∵BD=DC,
∴AF=BD,
∴四边形AFBD是平行四边形,
∴S四边形AFBD=2S△ABD,
又∵BD=DC,
∴S△ABC=2S△ABD,
∴S四边形AFBD=S△ABC,
∵∠BAC=90°,tan∠ACB=,AB=4,
∴AC==6,
∴S△ABC=AB?AC=×4×6=12,
∴S四边形AFBD=12.
故答案为:12.
13.【解答】解:如图,点C关于OA的对称点C′(﹣1,0),点C关于直线AB的对称点C″,
∵直线AB的解析式为y=﹣x+7,
∴直线CC″的解析式为y=x﹣1,
由解得,
∴直线AB与直线CC″的交点坐标为K(4,3),
∵K是CC″中点,
∴可得C″(7,6).
连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,
△DEC的周长=DE+EC+CD=EC′+ED+DC″=C′C″==10.
故答案为10.
14.【解答】解:由主视图和左视图可得每一层的每一行每一列都要保留一个立方体,
故取走的小立方体最多可以是4个.
具体可参看图形:
故答案为:4.
三、解答下列各题:
15.【解答】解:(1)
解不等式①,得x≤﹣1,
解不等式②,得x≤3,
故原不等式组的解集是x≤﹣1;
(2)÷()
=÷
=?
=.
16.【解答】解:如图所示:
,
由树状图可得:一共有20种可能,两球同色的有8种情况,故选择甲的概率为:=;
则选择乙的概率为:,
故此游戏不公平.
17.【解答】解:(1)由条形图知,男生共有:10+20+13+9=52人,
∴女生人数为100﹣52=48人,
∴参加武术的女生为48﹣15﹣8﹣15=10人,
∴参加武术的人数为20+10=30人,
∴30÷100=30%,
参加器乐的人数为9+15=24人,
∴24÷100=24%,
补全条形统计图和扇形统计图如图所示:
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是.
答:在参加“剪纸”活动项目的学生中,男生所占的百分比为40%.
(3)500×21%=105(人).
答:估计其中参加“书法”项目活动的有105人.
(4).
答:正好抽到参加“器乐”活动项目的女生的概率为.
18.【解答】解:过点D作水平线的垂线,即(DE⊥AB),垂足为E,则C、D、E在一条直线上,
设DE的长为x米,
在Rt△BCE中,∠CBE=45°,
∴CE=BE=CD+DE=(10+x)米,
在Rt△ADE中,∠A=35°,
AE=AB+BE=20+10+x=30+x,
tanA=,
∴tan35°=≈,
解得:x≈70,
答:假山的高度DE约为70米.
19.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠AFC=∠DCG,
∵GA=GD,∠AGF=∠CGD,
∴△AGF≌△DGC,
∴AF=CD,
∴AB=AF.
(2)解:结论:四边形ACDF是矩形.
理由:∵AF=CD,AF∥CD,
∴四边形ACDF是平行四边形,
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD=120°,
∴∠FAG=60°,
∵AB=AG=AF,
∴△AFG是等边三角形,
∴AG=GF,
∵△AGF≌△DGC,
∴FG=CG,∵AG=GD,
∴AD=CF,
∴四边形ACDF是矩形.
20.【解答】解:(1)设今年A型车每辆售价x元,则去年售价每辆为(x+400)元,由题意,得:
=,
解得:x=1600.
经检验,x=1600是原方程的根.
答:今年A型车每辆售价1600元;
(2)设今年新进A型车a辆,则B型车(60﹣a)辆,由题意,得
(1600﹣1100)a+(2000﹣1400)(60﹣a)≥33000,
解得:a≤30,
故要使这批车获利不少于33000元,A型车至多进30辆.
21.【解答】解:(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;
(2)设线段AB所表示的y1与x之间的函数关系式为y=k1x+b1,
∵y=k1x+b1的图象过点(0,60)与(90,42),
∴,
∴解得:,
∴这个一次函数的表达式为;y=﹣0.2x+60(0≤x≤90);
(3)设y2与x之间的函数关系式为y=k2x+b2,
∵经过点(0,120)与(130,42),
∴,
解得:,
∴这个一次函数的表达式为y2=﹣0.6x+120(0≤x≤130),
设产量为xkg时,获得的利润为W元,
当0≤x≤90时,W=x[(﹣0.6x+120)﹣(﹣0.2x+60)]=﹣0.4(x﹣75)2+2250,
∴当x=75时,W的值最大,最大值为2250;
当90≤x≤130时,W=x[(﹣0.6x+120)﹣42]=﹣0.6(x﹣65)2+2535,
由﹣0.6<0知,当x>65时,W随x的增大而减小,∴90≤x≤130时,W≤2160,
∴当x=90时,W=﹣0.6(90﹣65)2+2535=2160,
因此当该产品产量为75kg时,获得的利润最大,最大值为2250.
故答案为:w=﹣0.4(x﹣75)2+2250;w=﹣0.6(x﹣65)2+2535,75,2250.
22.【解答】解:(1)由题意CQ=AQ=8﹣2t,
在Rt△BCQ中,∵BC2+BQ2=CQ2,
∴62+(2t)2=(8﹣2t)2,
解得t=.
(2)∵四边形ABCD是矩形,
∴S矩形ABCD=AB?BC=8×6=48,
∵PM⊥AD,CD⊥AD,
∴PM∥CD,
∴△APM∽△ACD,
∴==,
即 ==,
解得AM=t,PM=t,
∴S△APM=AM?PM=×t×t=t2.
∵sin∠PAQ==,
∴S△APQ=AP?AQ?sin∠PAQ=×2t(8﹣2t)×=t(4﹣t),
∵S四边形PQAM=t2+t(4﹣t)=﹣t2+t.
(3)存在t=2,使S四边形PQAM=S矩形ABCD.
如图2,
,
∵S四边形PQAM=S矩形ABCD,
∴t2+t(4﹣t)=×48,
整理,可得t2﹣20t+36=0
解得t=2或t=18(舍去),
∴存在t=2,使S四边形PQAM=S矩形ABCD.
(4)当t=2或1时,△APQ与△ABC相似.
①当△APQ∽△ACB,
∴=,
即 =,
解得t=2,
②如图3,
,
当∠APQ=90°时,△APQ与△ABC相似,
∵tan∠PAQ==,
∴=,
即 =,
∴PQ=t,
∵BQ=2t,
∴AQ=8﹣2t,
在Rt△APQ中,
∵AP2+PQ2=AQ2,
∴(2t)2+(t)2=(8﹣2t)2,
解得t=1或t=﹣16(舍去).
综上,可得
当t=2或1时,△APQ与△ABC相似.
同课章节目录
